线性代数本质理解回顾（四） 逆矩阵、列空间与零空间

此视频要通过线性变换来了解逆矩阵、列空间、秩和零空间的概念。

线性代数一个作用是解方程组  这是线性方程组+

 事实上，你可以将所有的方程合并为一个向量方程。这个方程有一个包含所有常数系数的矩阵。

 

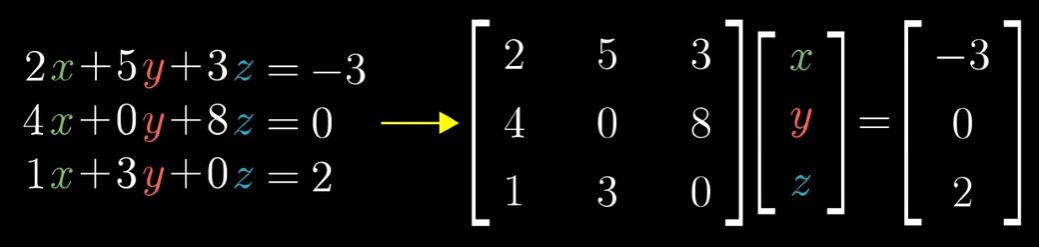
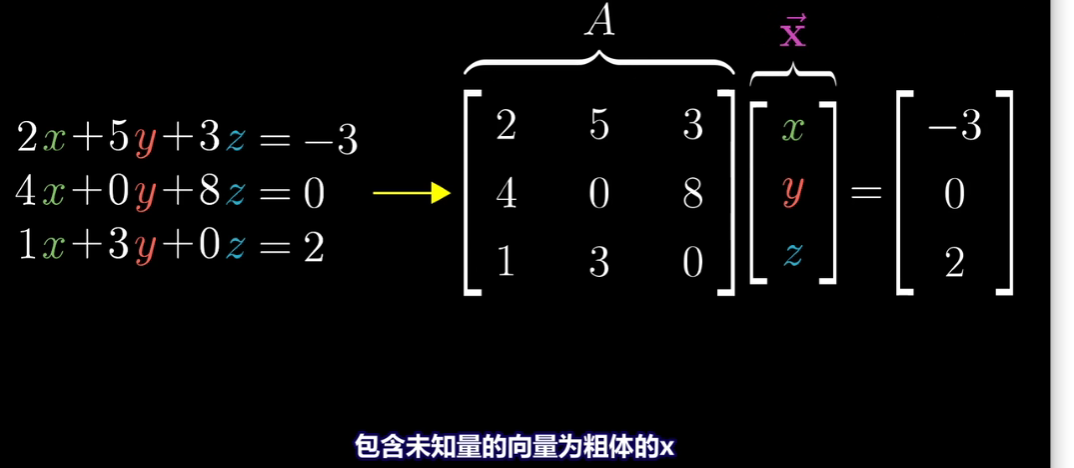
 这不仅仅是将方程组写进一行的书写技巧。还阐释了这个问题中优美的几何直观部分。

矩阵A代表一种线性变换，所以求解Ax=v意味着我们去寻找一个向量x，使得它在变换后与v重合。

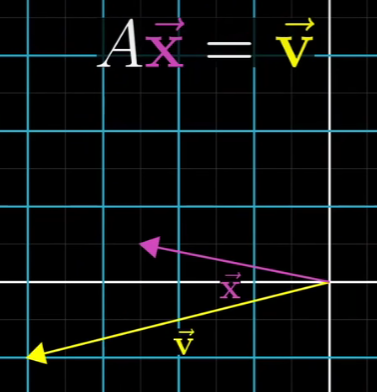
 思考下这一过程，你完全可以只考虑对空间变形，以及变换前后向量的重叠。

 

 

先举个简单的例子，你有两个方程和两个未知量构成的方程组，

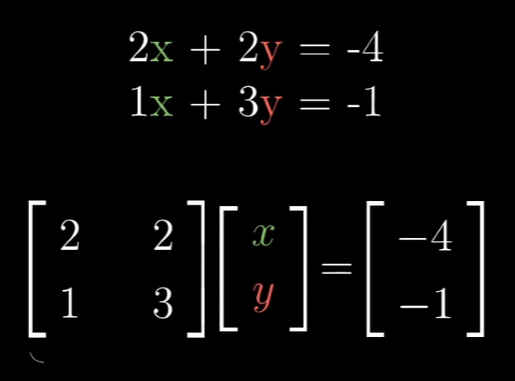
我们将它们分为两种情况，A的行列式为0，或A的行列式不为0

首先来看看最可能的情况，即A的行列式不为0.

此时空间并未呗挤压为0面积。

在这种情况下，有且仅有一个向量与v重合。

 并且你可以通过逆向进行变换来找到这个向量。如同倒带一样，通过跟踪v的动向，你就能找到满足Ax=v的向量x  。当你逆向进行变换时，它实际上对应了另一个线性变换，

通常被称为A的逆

 

 

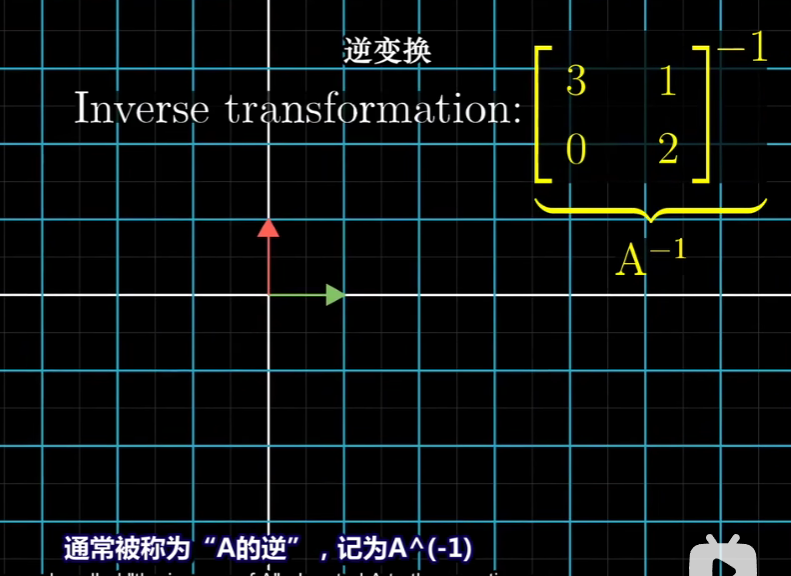
比如说，如果A是逆时针旋转90度的变换，那么A的逆就是顺时针90度的变换，

总的来说 A逆是满足以下性质的唯一变换。

应用A  然后A逆， 你会回到原始状态，两个变换相继作用在代数上体现为矩阵乘法，所以A逆的核心在于，A*A-1  = 单位阵（单位阵 什么都不做）

一旦你找到了A-1   你就能早两边同×A-1  来求解向量方程。

 

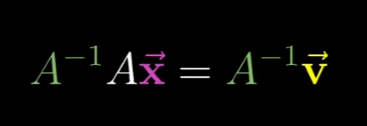
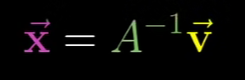
 这个过程在几何上就对应于逆向进行变换并跟踪v的动向。

 

 

当行列式为0时候····

除了0行列式之外，我们还有特定术语来描述它们，秩，当变幻的结果为一条直线时，也就是说结果是一维的，我们就称这个变换的秩为1.

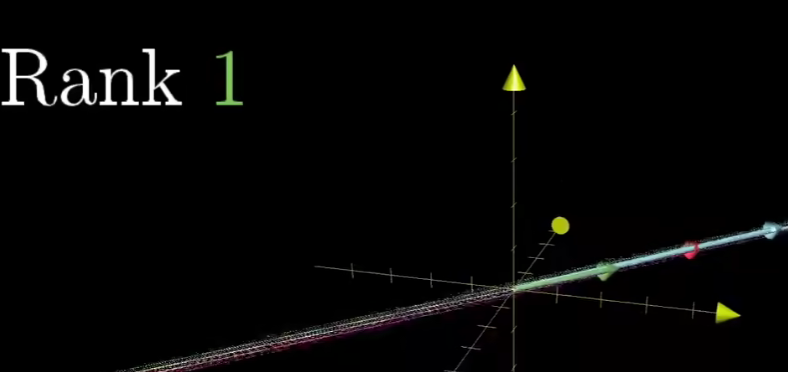
 如果变换后的向量落在一个二维平面上，我们称这个变换的秩为2.

 

所以说 秩 代表变换后空间的维数

 比如对于2*2的矩阵，它的秩最大为2.意味着基向量仍然能张成整个二维空间，并且矩阵的行列式不为0，但是对于3*3的矩阵，秩为2意味着空间被压缩了。但是和秩为1的情况相比，压缩并不那么严重。

如果一个三维变换的行列式为0，并且变换后结果仍充满整个三维空间，那么它的秩为3.（行列式为0？？？）  

 

不管是一条直线、一个平面还是三维空间等，所有可能的变换结果的集合，被称为矩阵的列空间。

 

你能猜到名字从哪来的，

矩阵的列告诉你基向量变换后的位置。

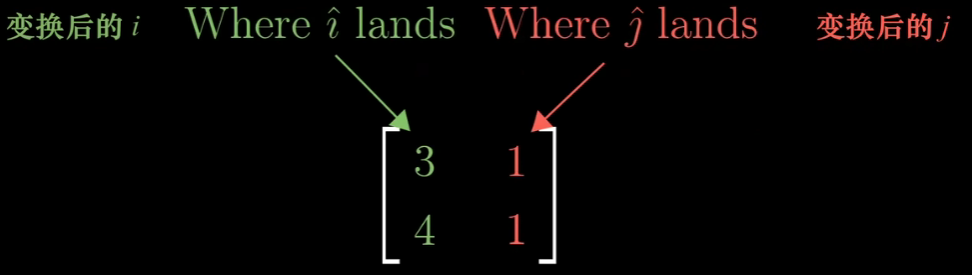
 这些变换后的基向量张成的空间就是所有可能的变化结果。换句话说，列空间就是矩阵的列所张成的空间。

 所以秩的更精确的定义是列空间的维数，

当秩达到最大时，意味着秩与列数相等。我们称之为 “满秩”

注意 零向量一定被包含在列空间中。因为线性变换必须保持原点位置不变，

 对于一个满秩变换来说，唯一能变换后落在远点的就是零向量自身。对于一个非满秩的矩阵来说，它将空间压缩到一个更低的维度上，也就是说会有一系列向量在变换后成为零向量。

 

举个例子，如果一个二维线性变换将空间压缩到一条直线上，那么沿一个不同方向直线上的所有向量就被压缩到原点，

在变换后落在原点的向量集合，被称为所选矩阵的零空间或核，变换后一些向量落在零向量上，从这个意义上说，零空间就是这些向量所构成的空间。

 

对线性方程组来说，当向量v恰好为零向量时，零空间给出的就是这个向量方程的所有可能解，

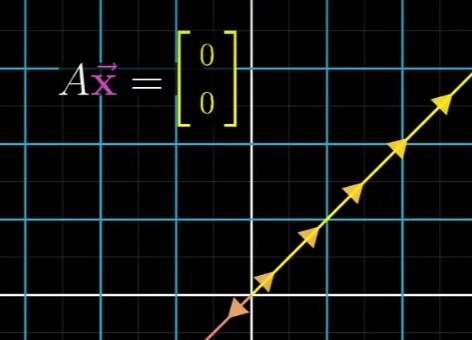
 以上就是从几何角度理解线性方程组的概述。