线性代数本质理解回顾(三) 行列式
内容来源:线性代数的本质 - 05 - 行列式_哔哩哔哩_bilibili
现在想象一些线性变换,你可能注意到其中有的空间向外拉伸,有的则向内挤压。


有件事对理解这些线性变换很有用。那就是测量变换究竟对空间有多少拉伸或挤压。更具体一点,就是测量一个给定区域面积增大或减小的比例。

以下面这个矩阵为例。

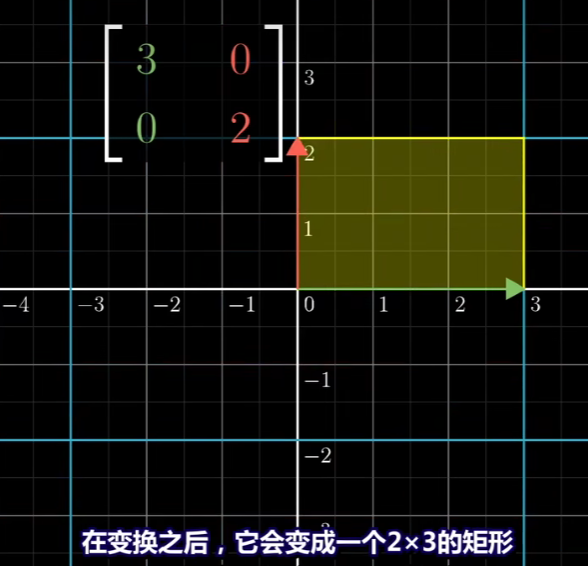
所以说这个线性变换将它的面积变为6倍。
剪切矩阵。

面积仍为1

实际上 你只需要知道这个单位正方形面积变化的比例,它就能告诉你其他任意区域的面积变化比例。这个特殊的缩放比例,即线性变换对面积产生改变的比例,被称为这个变换的行列式。

最后这个例子非常重要,只需要检验一个矩阵的行列式是否为0,就能了解这个矩阵所代表的变换是否能将空间压缩到更小的维度上。

现在说的并不完全正确。完整概念下的行列式是允许出现负值的。
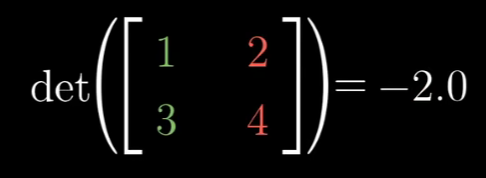
那将一个区域放缩到负数倍是什么意思?
这和去向的概念有关,举个例子,注意这个变换在感觉上将整个平面翻转了


就像一张纸翻了过来。
我们称这些类似的变换反转了空间去向。
另一种是考虑i帽和j帽的取向。变换之后 j帽处于i帽的右边。

行列式的绝对值依然表示区域面积的缩放比例。
那么负的面积缩放比例为什么会自然地用来描述取向翻转呢?

以上就是行列式在二维空间的理解。在三维空间是什么意思?是体积的缩放。
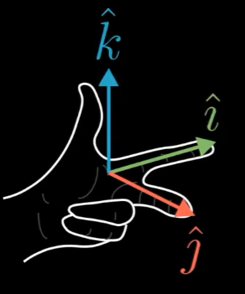
三维空间的负值行列式什么意思?有一种方法来描述三维空间的取向,那就是右手定则。

否则,在变换后你只能用左手这么做,说明空间发生翻转,行列式为负。
那么如何计算行列式?
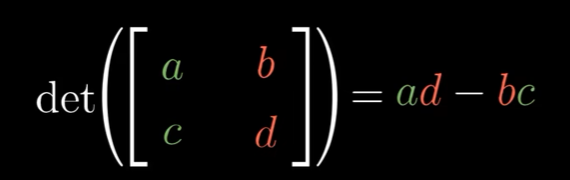
以下是直观理解。
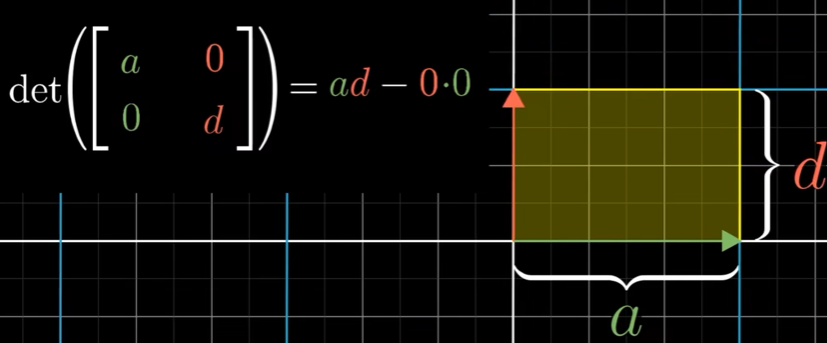
三维如何计算?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号