线性代数理解回顾（二）

矩阵乘法与线性变换复合

内容来源：【熟肉】线性代数的本质 - 04 - 矩阵乘法与线性变换复合_哔哩哔哩_bilibili

 

很多时候你想描述这样一种作用：一个变换之后再进行另外一个变换，比如说先将整个平面逆时针90度后，再进行一次剪切会发生什么， 

 从头到位的总体作用是另一个线性变换。这个新的线性变换通常被称为前两个独立变换的复合变换。

可以通过记录i与j的落脚点，用矩阵完全描述这个复合变换。

这一新的矩阵捕捉到了旋转然后剪切的总体效应，但它是一个单独的作用，而不是两个相继作用的合成。（可以理解，不是一步一步来的）

这里有种方法来考虑这个新矩阵，如果你有一个向量，将它进行旋转然后剪切，计算结果的一个麻烦的办法是：首先将它左乘旋转矩阵，

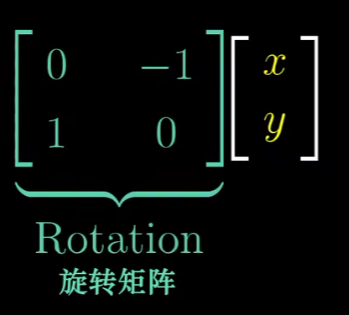
 得到结果再左乘 剪切矩阵

 

 

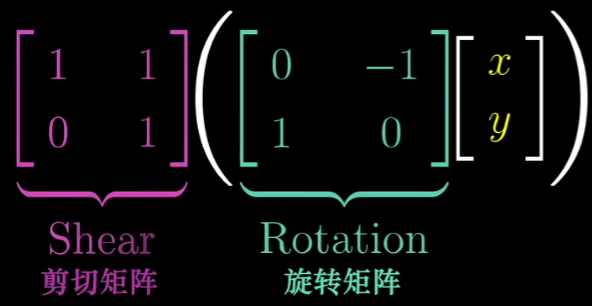
根据我们在这里写下的内容，我认为将这个新矩阵称为最初两个矩阵的积是合理的，不是吗？

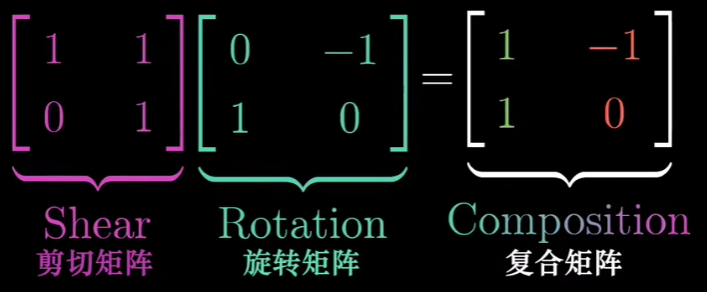
 我们很快就能搞清楚在更普遍的情况下如何计算这个乘积  但是这样太容易迷失在数字丛林当中。时刻记得 ，两个矩阵有几何意义，也就是两个线性变换相继作用。

 

这里有个奇怪的事，就是这个乘积要从右向左读。

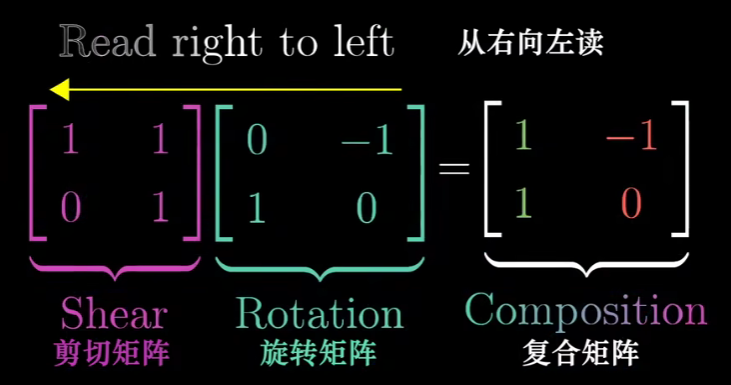
 首先应用右侧矩阵描述的变换，然后应用左侧。它起源于函数的记号，因为我们将函数卸载变量左侧。

 

再看一个例子，有一个矩阵

这次我们不看动画  只用每个矩阵的数值来求解。我们要找到 i帽的位置去哪了。

 

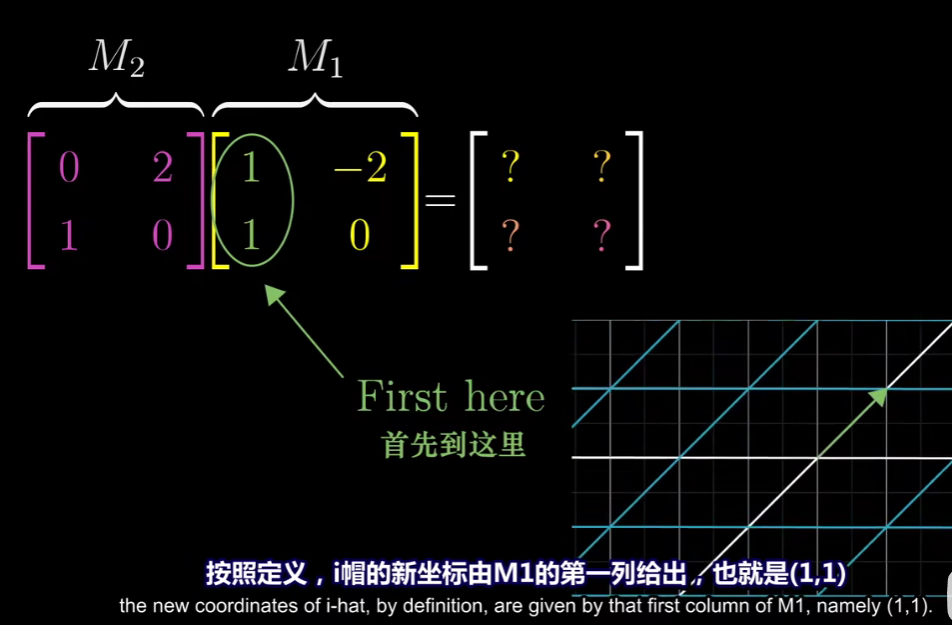
 同理看j帽去哪了，

 

 

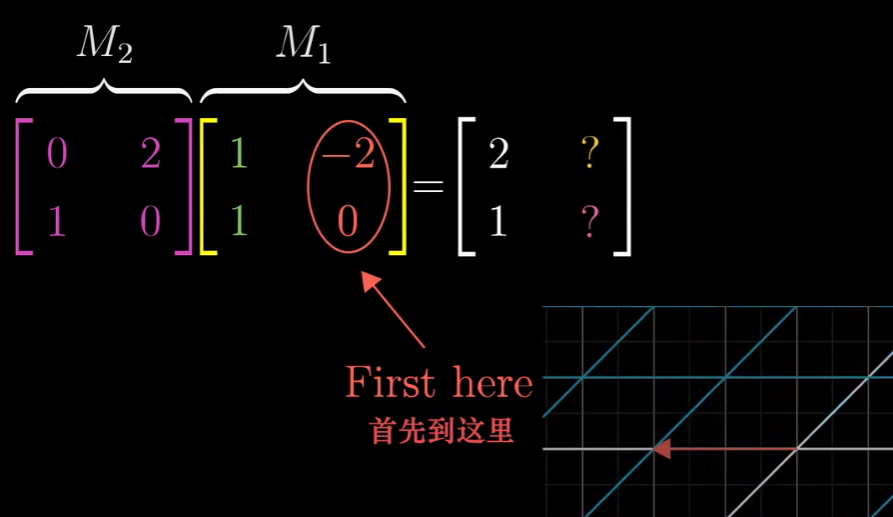
这一方法具有普适性。通常学生需要记住这个公式。

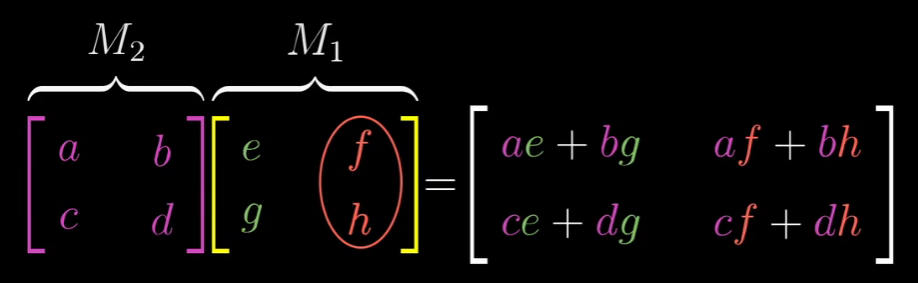
 我认为你应该养成思考矩阵乘法意义的习惯。

 

矩阵相乘顺序影响结果吗？

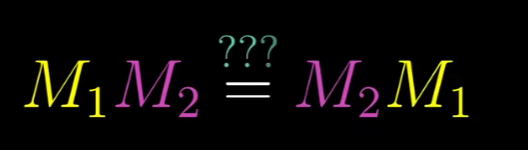
 先来一个简单的例子。 

 

 

上述视频只说明了一类将二维向量转换为其他二维向量的特殊变换。总体而言我们主要在二维空间进行展示。下面进行三维的展示。