生成文本中的解码策略

原文：如何生成文本：通过 Transformers 用不同的解码方法生成文本 (huggingface.co)

 

1.贪心搜索 greedy search

在每个时间步简单的选择概率最高的词作为当前输出词

 2.波束搜索 Beam search

波束搜索通过在每个时间步保留最可能的 num_beams 个词，并从中最终选择出概率最高的序列来降低丢失潜在的高概率序列的风险。以 num_beams=2 为例:

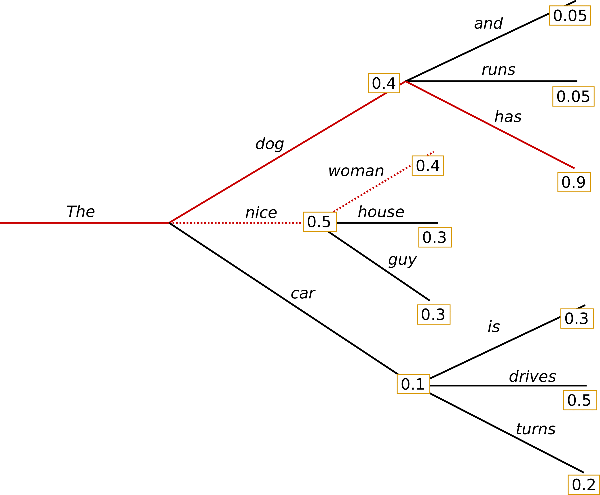
在时间步 1，除了最有可能的假设 $(\text{“The”}, \text{“nice”})$，波束搜索还跟踪第二可能的假设 $(\text{“The”}, \text{“dog”})$。在时间步 2，波束搜索发现序列 $(\text{“The”}, \text{“dog”}, \text{“has”})$ 概率为$0.36$，比 $(\text{“The”}, \text{“nice”}, \text{“woman”})$ 的 $0.2$ 更高。

 

波束搜索一般都会找到比贪心搜索概率更高的输出序列，但仍不保证找到全局最优解。

 

虽然结果比贪心搜索更流畅，但输出中仍然包含重复。一个简单的补救措施是引入 n-grams (即连续 n 个词的词序列) 惩罚，该方法是由 Paulus 等人 (2017) 和 Klein 等人 (2017) 引入的。最常见的 n-grams 惩罚是确保每个 n-gram 都只出现一次，方法是如果看到当前候选词与其上文所组成的 n-gram 已经出现过了，就将该候选词的概率设置为 0。

我们可以通过设置 no_repeat_ngram_size=2 来试试，这样任意 2-gram 不会出现两次:

不错，看起来好多了！我们看到生成的文本已经没有重复了。但是，n-gram 惩罚使用时必须谨慎，如一篇关于 纽约 这个城市的文章就不应使用 2-gram 惩罚，否则，城市名称在整个文本中将只出现一次！

波束搜索的另一个重要特性是我们能够比较概率最高的几个波束，并选择最符合我们要求的波束作为最终生成文本。

在 transformers 中，我们只需将参数 num_return_sequences 设置为需返回的概率最高的波束的数量，记得确保 num_return_sequences <= num_beams！

 

开放域文本生成的研究人员最近提出了几个理由来说明对该领域而言波束搜索可能不是最佳方案:

• 在机器翻译或摘要等任务中，因为所需生成的长度或多或少都是可预测的，所以波束搜索效果比较好 - 参见 Murray 等人 (2018) 和 Yang 等人 (2018) 的工作。但开放域文本生成情况有所不同，其输出文本长度可能会有很大差异，如对话和故事生成的输出文本长度就有很大不同。

• 我们已经看到波束搜索已被证明存在重复生成的问题。在故事生成这样的场景中，很难用 n-gram 或其他惩罚来控制，因为在“不重复”和最大可重复 n-grams 之间找到一个好的折衷需要大量的微调。

• 正如 Ari Holtzman 等人 (2019) 所论证的那样，高质量的人类语言并不遵循最大概率法则。换句话说，作为人类，我们希望生成的文本能让我们感到惊喜，而可预测的文本使人感觉无聊。论文作者画了一个概率图，很好地展示了这一点，从图中可以看出人类文本带来的惊喜度比波束搜索好不少。

 

采样

在其最基本的形式中，采样意味着根据当前条件概率分布随机选择输出词 $w_t$:

wt​∼P(w∣w1:t−1​)

继续使用上文中的例子，下图可视化了使用采样生成文本的过程。

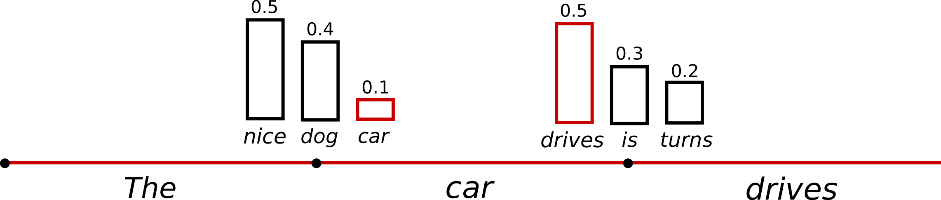
很明显，使用采样方法时文本生成本身不再是 确定性的。单词 $\text{“car”}$ 从条件概率分布 $P(w | \text{“The”})$ 中采样而得，而 $\text{“drives”}$ 则采样自 $P(w | \text{“The”}, \text{“car”})$。

在 transformers 中，我们设置 do_sample=True 并通过设置 top_k=0 停用 Top-K 采样 (稍后详细介绍)。在下文中，为便于复现，我们会固定 random_seed=0，但你可以在自己的模型中随意更改 random_seed。

 

有意思！生成的文本看起来不错 - 但仔细观察会发现它不是很连贯。3-grams new hand sense 和 local batte harness 非常奇怪，看起来不像是人写的。这就是对单词序列进行采样时的大问题: 模型通常会产生不连贯的乱码，参见 Ari Holtzman 等人 (2019) 的论文。

缓解这一问题的一个技巧是通过降低所谓的 softmax 的“温度”使分布 $P(w|w_{1:t-1})$ 更陡峭。而降低“温度”，本质上是增加高概率单词的似然并降低低概率单词的似然。

将温度应用到于我们的例子中后，结果如下图所示。

 

好，奇怪的 n-gram 变少了，现在输出更连贯了！虽然温度可以使分布的随机性降低，但极限条件下，当“温度”设置为 $0$ 时，温度缩放采样就退化成贪心解码了，因此会遇到与贪心解码相同的问题。

 

 

Top-K 采样

Fan 等人 (2018) 的论文介绍了一种简单但非常强大的采样方案，称为 Top-K 采样。在 Top-K 采样中，概率最大的 K 个词会被选出，然后这 K 个词的概率会被重新归一化，最后就在这重新被归一化概率后的 K 个词中采样。 GPT2 采用了这种采样方案，这也是它在故事生成这样的任务上取得成功的原因之一。

我们将上文例子中的候选单词数从 3 个单词扩展到 10 个单词，以更好地说明 Top-K 采样。

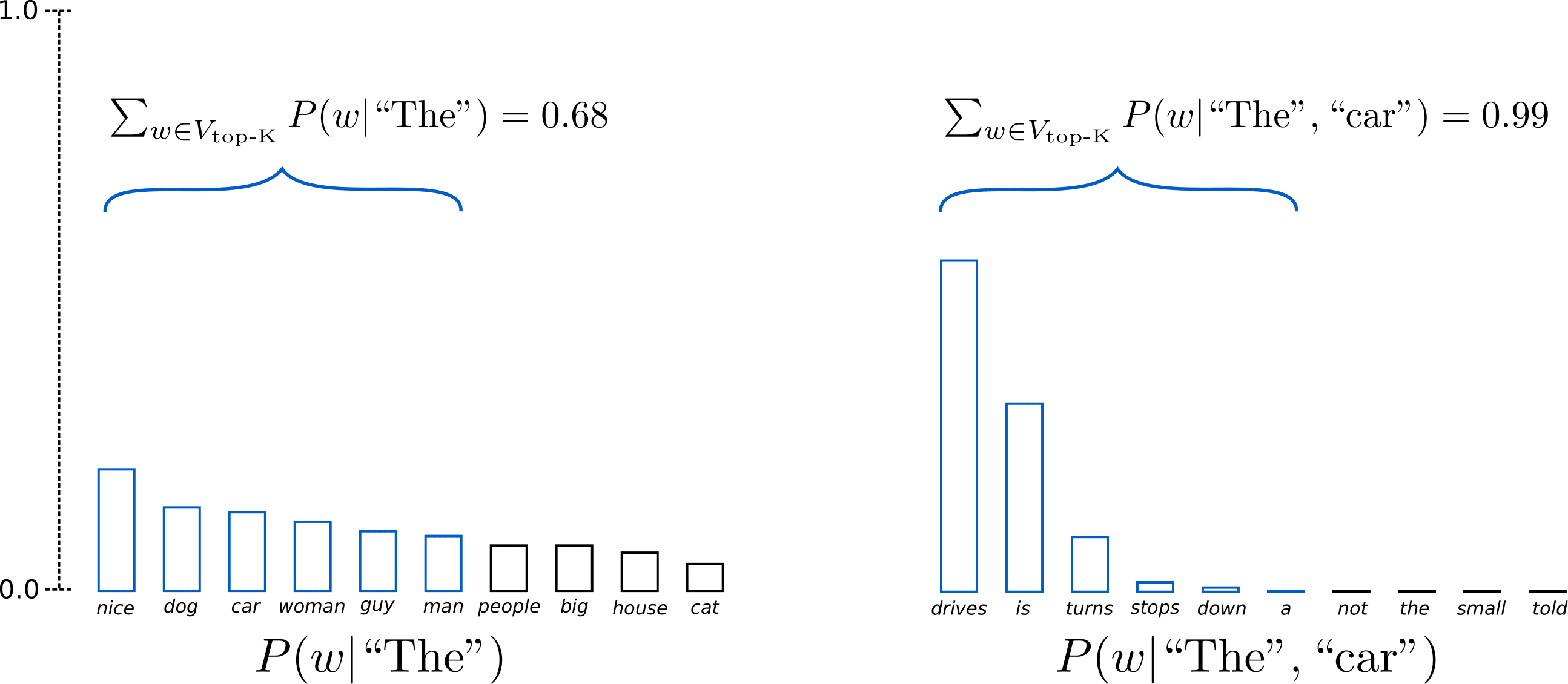
设 $K = 6$，即我们将在两个采样步的采样池大小限制为 6 个单词。我们定义 6 个最有可能的词的集合为 $V_{\text{top-K}}$。在第一步中，$V_{\text{top-K}}$ 仅占总概率的大约三分之二，但在第二步，它几乎占了全部的概率。同时，我们可以看到在第二步该方法成功地消除了那些奇怪的候选词 $(\text{“not”}, \text{“the”}, \text{“small”}, \text{“told”})$。

相当不错！该文本可以说是迄今为止生成的最 "像人" 的文本。现在还有一个问题，Top-K 采样不会动态调整从需要概率分布 $P(w|w_{1:t-1})$ 中选出的单词数。这可能会有问题，因为某些分布可能是非常尖锐 (上图中右侧的分布)，而另一些可能更平坦 (上图中左侧的分布)，所以对不同的分布使用同一个绝对数 K 可能并不普适。

在 $t=1$ 时，Top-K 将 $(\text{“people”}, \text{“big”}, \text{“house”}, \text{“cat”})$ 排出了采样池，而这些词似乎是合理的候选词。另一方面，在$t=2$ 时，该方法却又把不太合适的 $(\text{“down”}, \text{“a”})$ 纳入了采样池。因此，将采样池限制为固定大小 K 可能会在分布比较尖锐的时候产生胡言乱语，而在分布比较平坦的时候限制模型的创造力。这一发现促使 Ari Holtzman 等人 (2019) 发明了 Top-p- 或 核- 采样。

 

 

Top-p (核) 采样

在 Top-p 中，采样不只是在最有可能的 K 个单词中进行，而是在累积概率超过概率 p 的最小单词集中进行。然后在这组词中重新分配概率质量。这样，词集的大小 (又名 集合中的词数) 可以根据下一个词的概率分布动态增加和减少。好吧，说的很啰嗦，一图胜千言。

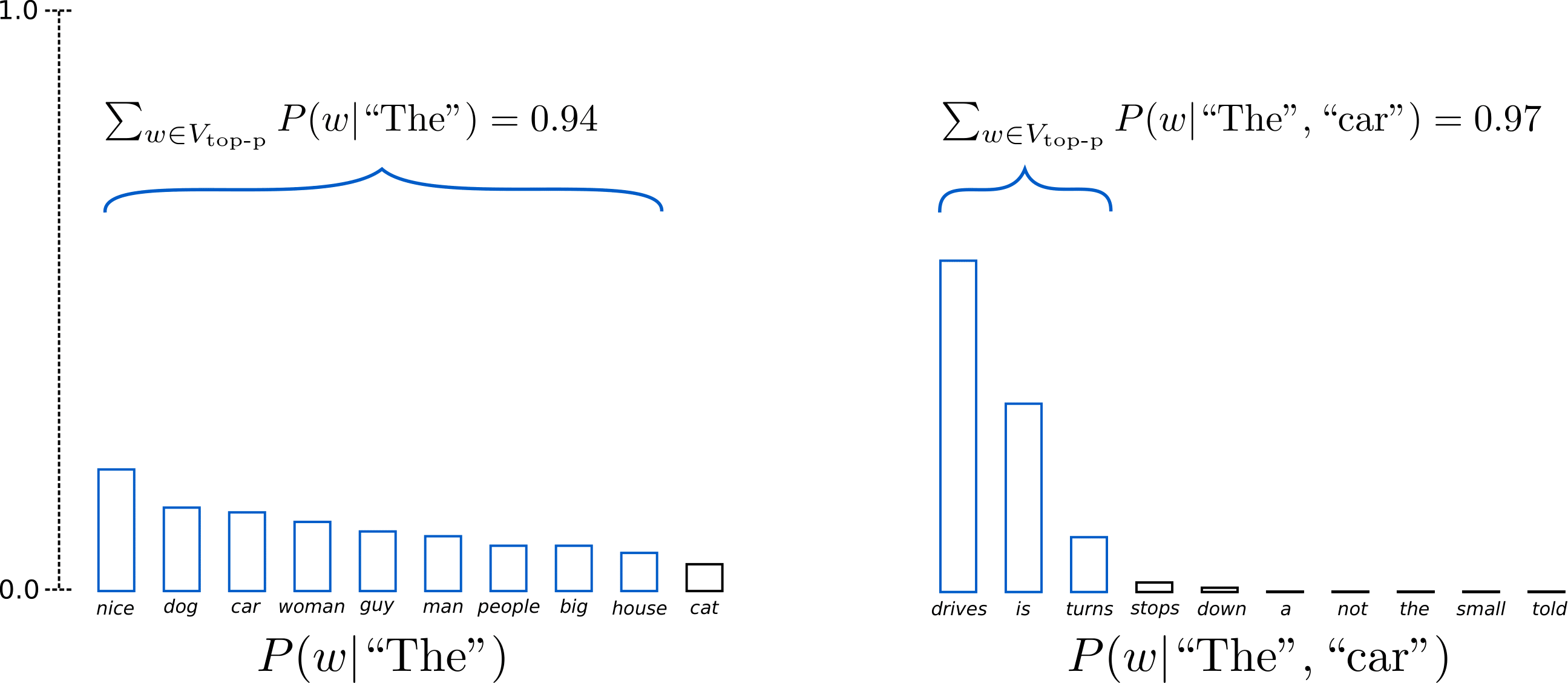
假设 $p=0.92$，Top-p 采样对单词概率进行降序排列并累加，然后选择概率和首次超过 $p=92%$ 的单词集作为采样池，定义为 $V_{\text{top-p}}$。在 $t=1$ 时 $V_{\text{top-p}}$ 有 9 个词，而在 $t=2$ 时它只需要选择前 3 个词就超过了 92%。其实很简单吧！可以看出，在单词比较不可预测时，它保留了更多的候选词，如 $P(w | \text{“The”})$，而当单词似乎更容易预测时，只保留了几个候选词，如 $P(w | \text{“The”}, \text{“car”})$。

 

 

 

总结

在开放域语言生成场景中，作为最新的解码方法， top-p 和 top-K 采样于传统的 贪心 和 波束 搜索相比，似乎能产生更流畅的文本。但，最近有更多的证据表明 贪心 和 波束 搜索的明显缺陷 - 主要是生成重复的单词序列 - 是由模型 (特别是模型的训练方式) 引起的，而不是解码方法， 参见 Welleck 等人 (2019) 的论文。此外，如 Welleck 等人 (2020) 的论文所述，看起来 top-K 和 top-p 采样也会产生重复的单词序列。

在 Welleck 等人 (2019) 的论文中，作者表明，根据人类评估，在调整训练目标后，波束搜索相比 Top-p 采样能产生更流畅的文本。

开放域语言生成是一个快速发展的研究领域，而且通常情况下这里没有放之四海而皆准的方法，因此必须了解哪种方法最适合自己的特定场景。

好的方面是， 你 可以在 transfomers 中尝试所有不同的解码方法 🤗