「JOISC 2018 Day 2」修行

Problem

「JOISC 2018 Day 2」修行

Solution

转化题意, 已知n k, 题目要 求所有排列中, 满足\(k-1=\sum\limits_{i=1}^{n-1} [a_i>a_{i+1}]\) 的排列的个数

考虑一个序列\(A=\{a_1,a_2...a_n\}, a_i\in [0,1)\)

其满足\(k-1=\sum\limits_{i=1}^{n-1} [a_i>a_{i+1}]\)的概率

等于n的全排列中满足要求的概率

此处省略证明

考虑构造一个序列\(B=\{b_1,b_2...b_n\}, b_i\in [0,1)\)

其中\(b_i=[a_{i-1}>a_i]+a_i-a_{i-1}\)

所以问题就转化为\(k-1<=\sum b_i<k\)的概率

考虑建立n维坐标系

则问题再次转化为:

在\((0,0...0)\)到\((1,1...1)\)的超立方体中等概率第取一个点, 记为\((c_1,c_2...c_n)\)

设\(f(k)\)为这个点满足\(\sum c_i < k\)的概率(注意此时还满足\(c_i<1\))

则答案为\((f(k)-f(k-1))n!\)

而\(f(k)\)正是超立方体被超平面\(\theta :\sum c_i =k\)切割后的体积与原体积之比(原体积就是1)

下图是n=2,k=1.5时的情况(k只能是个整数, k=1.5方便理解), 红色表示符合条件的概率

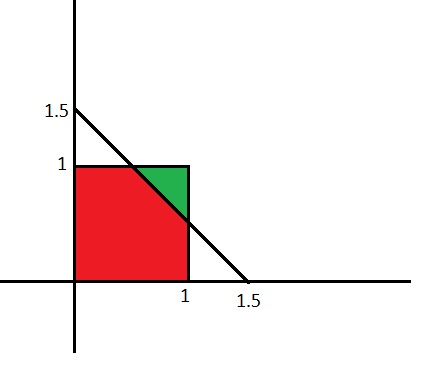
其中超平面与坐标轴形成的图形(三角形)体积(面积)为\(\frac{k^n}{n!}\)

然后红色面积为...

这个好像算不出来...

考虑容斥

g(x) 表示:

"在超平面与坐标轴形成的n维图形(上图中的三角形)中取一点

点的坐标中至少有 x 个维度 >=1(即不在超立方体内)的概率."

这 x 维的取值在[1,k)之间, 底边相等高不变, 钦点其减一变成[0,k-1), 对体积(面积)不造成影响

则总限制变成了 \(\sum c_i<k-x\)

所以\(g(x)=C_n^x \frac{(k-x)^n}{n!}\)

容斥:

\[f(k)=\sum_{i=0}^{k-1}(-1)^i g(i) \]

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
    for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';
    return x*f;
}
const int N=1e5+28,p=1e9+7;
int Pow(int x,int y){
    int re=1;
    while(y){
        if(y&1)re=re*x%p;
        x=x*x%p;
        y>>=1;
    }
    return re;
}
int n,k,prod[N],inv[N];
void Pre(){
    prod[0]=prod[1]=inv[0]=inv[1]=1;
    for(int i=2;i<=1e5;i++){
        prod[i]=prod[i-1]*i%p;
        inv[i]=(p-p/i)*inv[p%i]%p;
    }
    for(int i=2;i<=1e5;i++)inv[i]=inv[i]*inv[i-1]%p;
}
int C(int n,int m){return prod[n]*inv[m]%p*inv[n-m]%p;}
int Calc(int k){
    int re=0;
    for(int i=0;i<k;i++){
        int tmp=Pow(k-i,n)*inv[n]%p;
        tmp=tmp*C(n,i)%p;
        re=(re+((i&1)?p-1:1)*tmp%p)%p;
    }
    return re*prod[n]%p;
}
signed main(){
    Pre();
    n=read(),k=read();
    // if(n==3&&k==2)puts("fuck pps");
    printf("%lld",(p+Calc(k)-Calc(k-1))%p);
    return 0;
}