基数排序

【基本思想】

　　将所有待排序的数统一为相同的数位长度，数位较短的数前面补零，然后从低位到高位按位比较，位数字小的排在前面，大的排在后面，这样当比较第N位时前N-1位都是有序的，如此循环的比较，直到最高位比较完成，整个序列就是有序的了。

基数排序图文说明

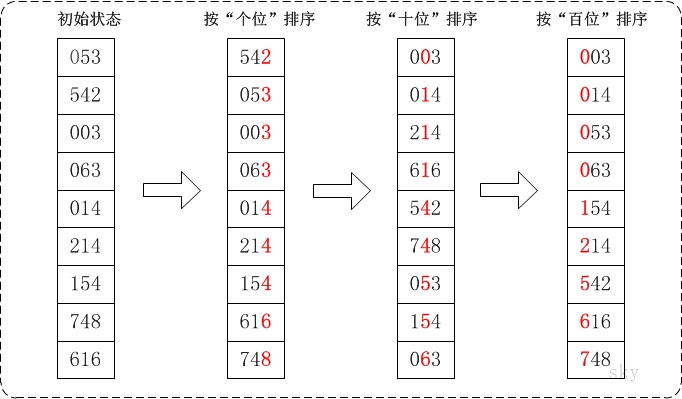
通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}，它的示意图如下：

在上图中，首先将所有待比较数字统一为相同的长度，接着从最低位开始，依次进行排序。
1. 按照个位数进行排序。
2. 按照十位数进行排序。
3. 按照百位数进行排序。
排序后，数列就变成了一个有序序列。

 

【算法复杂度】

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(d(r+n))	O(d(r+n))	O(d(r+n))	O(rd+n)	稳定

 

时间复杂度>>>

　　设待排序列为n个记录，序列中最大值的位数为d，数字的基数为 r，则进行链式基数排序的时间复杂度为O(d(n+r))。当分配数字时要对每一个数字进行按位比较， 而收集数字时要进行r次收集（如十进制数字就要进行从0到9共10次收集操作）， 故一趟分配时间复杂度为O(n)，一趟收集时间复杂度为O(r)，共进行d趟分配和收集。

算法稳定性>>>

　　因为基数排序是基于数字的位来排序的，所以排序过程中，当两个数字相同时，总是前一个数字率先被分配，并率先被收集起来，所以基数排序是稳定的排序算法

 

【动图演示】

 

【算法实现】

/*
** 基数排序的C++实现
** 假设：对N个整数进行升序排序
** 循环的将相同位的数字分配到同一个的链表中
** 当最高位比较完成时，全部的数据会被分配到P[0]中
*/

void RadixSort(vector<int>& seq){
    list<int> p[10];  // 用于存储每次分配数字的链表
    int k = 1, nums = 0;

    while (nums != seq.size()){ // 当记录没有全部存储到P[0]时
        for (int h = 0; h < seq.size(); h++){ // 开始按位分配数字
            int m = (seq[h] / k) % 10;
            p[m].push_back(seq[h]);  // 将数字压入其对应的链表中
        }
        seq.clear();
        nums = int(p[0].size()); // nums设置为P[0]的大小
        for (int i = 0; i < 10; i++){
            while (p[i].size()){ // 将刚刚分配的数字按顺序收集起来
                seq.push_back(p[i].front());
                p[i].pop_front();
            }
        }
        k = k * 10;
    }
}