快速排序

【基本思想】

　　首先选取一个初始值（一般选取待排序序列的第一个值），通过一趟排序将待排序序列分成两个子序列，使左子序列的所有数据都小于这个初始值，右子序列的所有数据都大于这个初始值，然后再按此方法分别对这两个子序列进行排序，递归的进行上面的步骤，直至每一个数据项都有如下性质：该数据项左边的数据都小于它，右边的数据都大于它，这样，整个序列就有序了。

　　设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。

一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

3）从i开始向后搜索，即由前开始向后搜索( i++ )，找到第一个大于key的A[i]；

4）从j开始向前搜索，即由后开始向前搜索( j-- )，找到第一个小于key的值A[j]；

5）将A[i]和A[j]互换；

5）重复第3、4、5步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[i]不大于key,4中A[j]不小于key的时候改变i、j的值，使得j=j-1，i=i+1，直至找到为止）。

 

【算法复杂度】

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(nlogn)	O(n^2)	O(nlogn)	O(1)	不稳定

   

 

【动图演示】

 

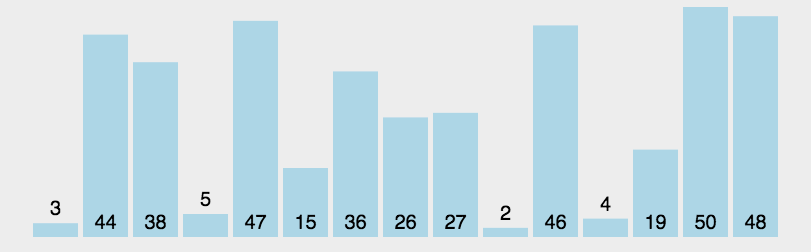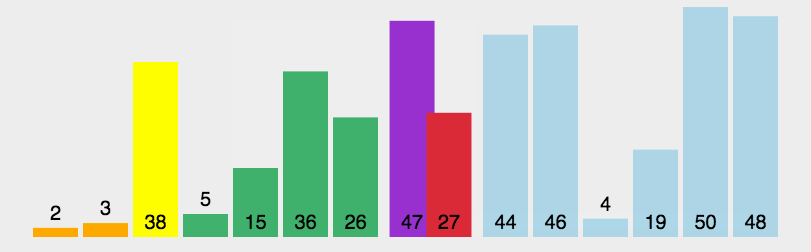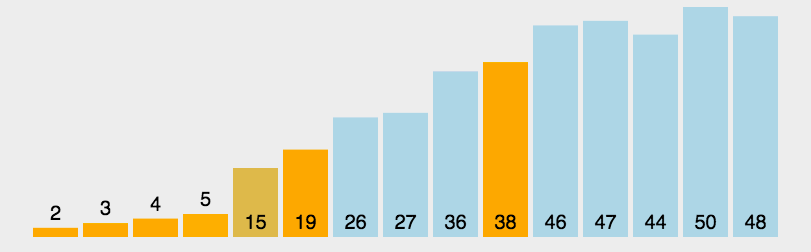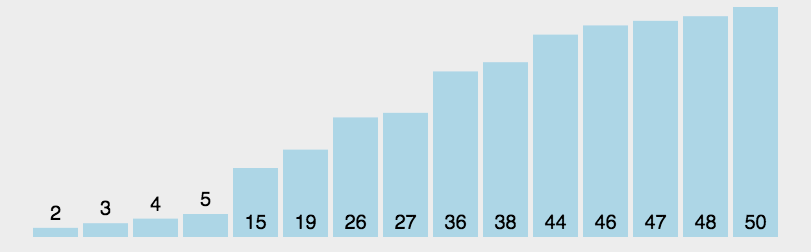
【算法实现】

/*
** 快速排序算法的C++实现
** 假设：对有限个INT类型数据进行升序排序
** swap()函数：交换序列中两个数的位置
** partition()函数：切分待排序序列，
** 使切分后的两个子序列满足左子序列小于右子序列
** Qsort()函数：递归的进行切分操作
*/

void swap(vector<int>& seq, int low, int high) {
    int temp = seq[low];
    seq[low] = seq[high];
    seq[high] =  temp;
}

int partition(vector<int>& seq, int low, int high) {
    int pivotkey = seq[low], pindex = low; // pivotkey为初始值，pindex为初始值的索引
    while (low < high) {
        while (low < high && seq[high] >= pivotkey) high--; // 从右向左扫描，找到第一个小于初始值的数据项
        while (low < high && seq[low] <= pivotkey) low++; // 从左向右扫描，找到第一个大于初始值的数据项
        swap(seq, low, high);   // 交换两个数据项
    }
    swap(seq, pindex, low); // 将初始值存放到正确的位置
    return low;
}

void QSort(vector<int>& seq, int low, int high) {
    if (low < high) {
        int pivot = partition(seq, low, high);
        QSort(seq, low, pivot - 1);  // 对左子序列递归的进行切分操作
        QSort(seq, pivot + 1, high);  // 对右子序列递归的进行切分操作
    }
}

void QuickSort(vector<int>& seq) {
    QSort(seq, 0, seq.size() - 1);
}

 

【算法优化】

三平均分区法

　　 每次尽可能地选择一个能够代表中值的元素作为关键数据，然后遵循普通快排的原则进行比较、替换和递归。通常来说，选择这个数据的方法是取开头、结尾、中间3个数据，通过比较选出其中的中值。取这3个值的好处是在实际问题中，出现近似顺序数据或逆序数据的概率较大，此时中间数据必然成为中值，而也是事实上的近似中值。万一遇到正好中间大两边小（或反之）的数据，取的值都接近最值，那么由于至少能将两部分分开，实际效率也会有2倍左右的增加，而且利于将数据略微打乱，破坏退化的结构。

　　这一改进对于原来的快速排序算法来说，主要有两点优势：
　　（1） 首先，它使得最坏情况发生的几率减小了。
　　（2） 其次，未改进的快速排序算法为了防止比较时数组越界，在最后要设置一个哨点。

/*
** 三平均分区法
** 只需修改切分函数
*/

#define MAX(a, b)   (((a) > (b) ) ? (a) : (b))
#define MIN(a, b)   (((a) < (b) ) ? (a) : (b))
#define MID(a,b,c)  (MAX(a,b)>c?MAX(MIN(a,b),c):MIN(MAX(a,b),c))

int partition(vector<int>& seq, int low, int high) {
    int median = MID(low,high,(low+high)/2);  // 选择序列最左边、最右边、中间这三个数的中位数
    int s = ( median == seq[low]?low:(median == seq[high]?high:(low+high)/2) ); // 判断中位数的下标
    int pivotkey = seq[s], pindex = low;
    swap(seq,low,s); // 将中位数与最左边的数互换位置
    while (low < high) {
        while (low < high && seq[high] >= pivotkey) high--;
        while (low < high && seq[low] <= pivotkey) low++;
        swap(seq, low, high);
    }
    swap(seq, pindex, low);
    return low;
}

 

根据分区大小调整算法

　　这一方面的改进是针对快速排序算法的弱点进行的。快速排序对于小规模的数据集性能不是很好，可能有人认为可以忽略这个缺点不计，因为大多数排序都只要考虑大规模的适应性就行了。但是快速排序算法使用了分治技术，最终来说大的数据集都要分为小的数据集来进行处理。由此可以得到的改进就是，当数据集较小时，不必继续递归调用快速排序算法，而改为调用其他的对于小规模数据集处理能力较强的排序算法来完成。
　　另一种优化改进是当分区的规模达到一定小时，便停止快速排序算法，也即快速排序算法的最终产物是一个“几乎”排序完成的有序数列，数列中有部分元素并没有排到最终的有序序列的位置上，但是这种元素并不多，可以对这种“几乎”完成排序的数列使用插入排序算法进行排序以最终完成整个排序过程。因为插入排序对于这种“几乎”完成的排序数列有着接近线性的复杂度。这一改进被证明比持续使用快速排序算法要有效的多。

/*
** 根据区间动态调整排序算法
** 当区间小于一个阈值时停止快速排序，
** 使序列基本有序，然后对整个基本有序的序列进行插入排序
*/

int partition(vector<int>& seq, int low, int high) {
    if(high - low < 15) // 当区间小于一个阈值时停止快速排序
        return -1;
    int pivotkey = seq[low], pindex = low;
    while (low < high) {
        while (low < high && seq[high] >= pivotkey) high--;
        while (low < high && seq[low] <= pivotkey) low++;
        swap(seq, low, high);
    }
    swap(seq, pindex, low);
    return low;
}

void QSort(vector<int>& seq, int low, int high) {
    if (low < high) {
        int pivot = partition(seq, low, high);
        if (pivot + 1) {
            QSort(seq, low, pivot - 1);
            QSort(seq, pivot + 1, high);
        }
    }
}

void QuickSort(vector<int>& seq) {
    QSort(seq, 0, seq.size() - 1);
    insertSort(seq); // 调用插入排序算法对整个基本有序的序列进行排序
}

 

三向切分快速排序

　　快速排序在实际应用中会面对大量具有重复元素的数组，例如假如一个子数组全部为重复元素，则对于此数组排序就可以停止，但快排算法依然将其切分为更小的数组，这就造成时间上的浪费。

　　一个简单的想法就是将数组分为三部分：小于当前切分元素的部分，等于当前切分元素的部分，大于当前切分元素的部分。

　　E.W.Dijlstra提出的算法是： 对于每次切分，从数组的左边到右边遍历一次，维护三个指针，其中lt指针使得元素（seq[low]-seq[lt-1]）的值均小于切分元素；gt指针使得元素（seq[gt+1]-seq[high]）的值均大于切分元素；i指针使得元素（seq[lt]-seq[i-1]）的值均等于切分元素，（seq[i]-seq[gt]）的元素还为确定，切分算法执行到i>gt为止。

　　每次切分之后，位于gt指针和lt指针之间的元素的位置都已经被排定，不需要再去处理了。之后将（lo,lt-1）,（gt+1,hi）分别作为处理左子数组和右子数组的递归函数的参数传入，递归结束，整个算法也就结束。

/*
** 维护三个指针：
** 维护一个指针lt使 seq[low,lt-1] 中的元素都小于pivotkey
** 维护一个指针gt使 seq[gt+1,high]中的元素都大于pivotkey
** 维护一个指针i使  seq[lt,i-1]   中的元素都等于pivotkey
** 而seq[i,gt]中的元素都还为确定
** 注意：此算法只在序列中含有大量重复数据时能发挥作用，否则慢于传统的快速排序
*/

void QSort(vector<int>& seq, int low, int high) {
    if (low < high) {
        int lt = low, gt = high, i = low + 1, pivotkey = seq[low];
        while (i <= gt) {
            if(seq[i] < pivotkey)
                swap(seq, lt++, i++);
            else if(seq[i] > pivotkey) //
                swap(seq, i, gt--);
            else i++;
        }
        QSort(seq, low, lt - 1);  // 对左子序列递归的进行切分操作
        QSort(seq, gt + 1, high);  // 对右子序列递归的进行切分操作
    }
}

 

随机化快排

        快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元，这样在数组已经有序的情况下，每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法，即随机选取一个元素作为主元，这种情况下虽然最坏情况仍然是O(n^2)，但最坏情况不再依赖于输入数据，而是由于随机函数取值不佳。实际上，随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。一位前辈做出了一个精辟的总结：“随机化快速排序可以满足一个人一辈子的人品需求。”

　　随机化快速排序的唯一缺点在于，一旦输入数据中有很多的相同数据，随机化的效果将直接减弱。对于极限情况，即对于n个相同的数排序，随机化快速排序的时间复杂度将毫无疑问的降低到O(n^2)。解决方法是用一种方法进行扫描，使没有交换的情况下主元保留在原位置。

 

并行的快速排序

　　由于快速排序算法是采用分治技术来进行实现的，这就使得它很容易能够在多台处理机上并行处理。
　　在大多数情况下，创建一个线程所需要的时间要远远大于两个元素比较和交换的时间，因此，快速排序的并行算法不可能为每个分区都创建一个新的线程。一般来说，会在实现代码中设定一个阀值，如果分区的元素数目多于该阀值的话，就创建一个新的线程来处理这个分区的排序，否则的话就进行递归调用来排序。
　　对于这一并行快速排序算法也有其改进。该算法的主要问题在于，分区的这一步骤总是要在子序列并行处理之前完成，这就限制了整个算法的并行程度。解决方法就是将分区这一步骤也并行处理。改进后的并行快速排序算法使用2n个指针来并行处理分区这一步骤，从而增加算法的并行程度。