归并排序

【基本思想】

　　归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用，将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序。

　　归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

归并排序主要分为两部分： 1、划分子区间；2、合并子区间

合并相邻有序子序列

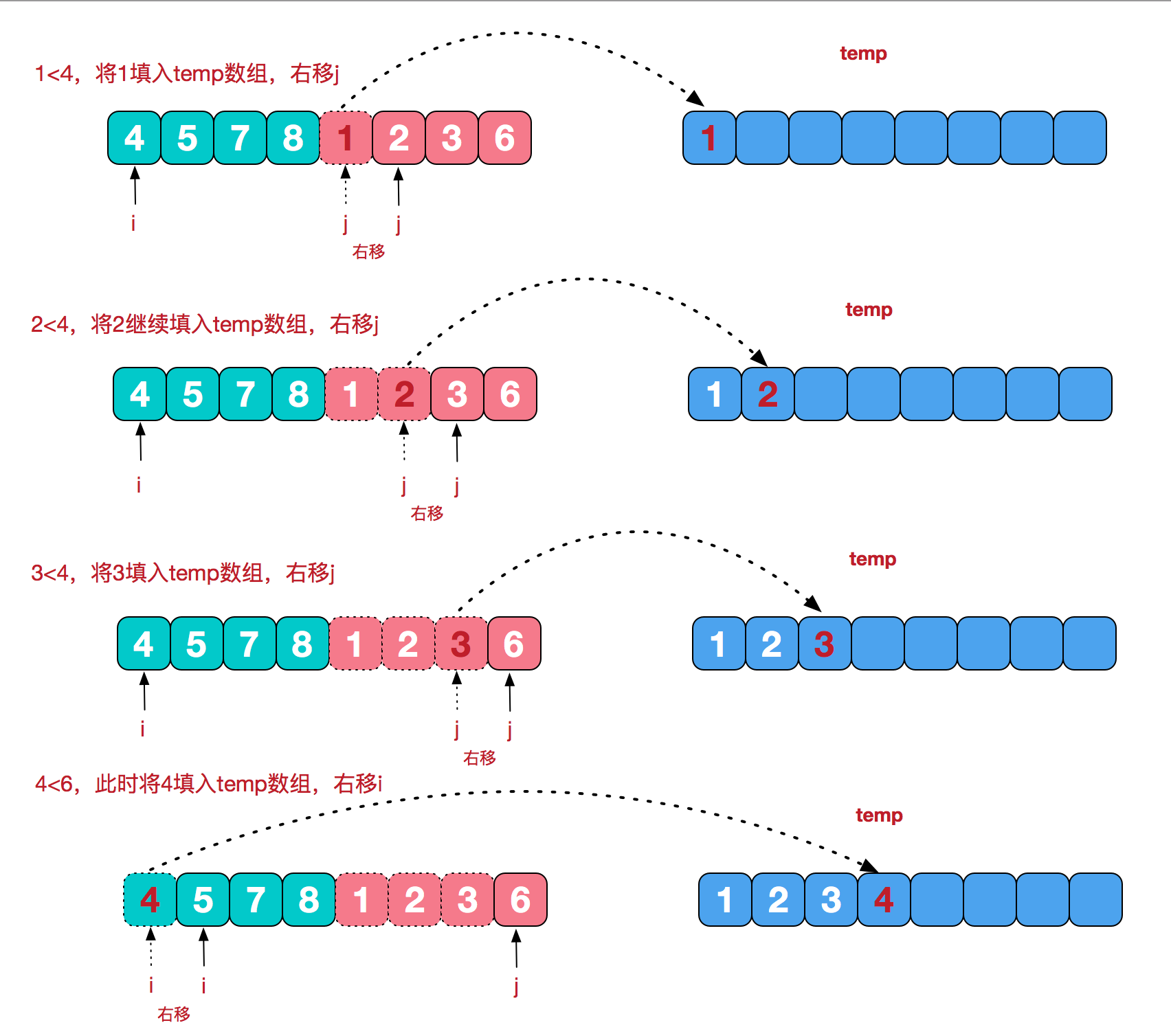
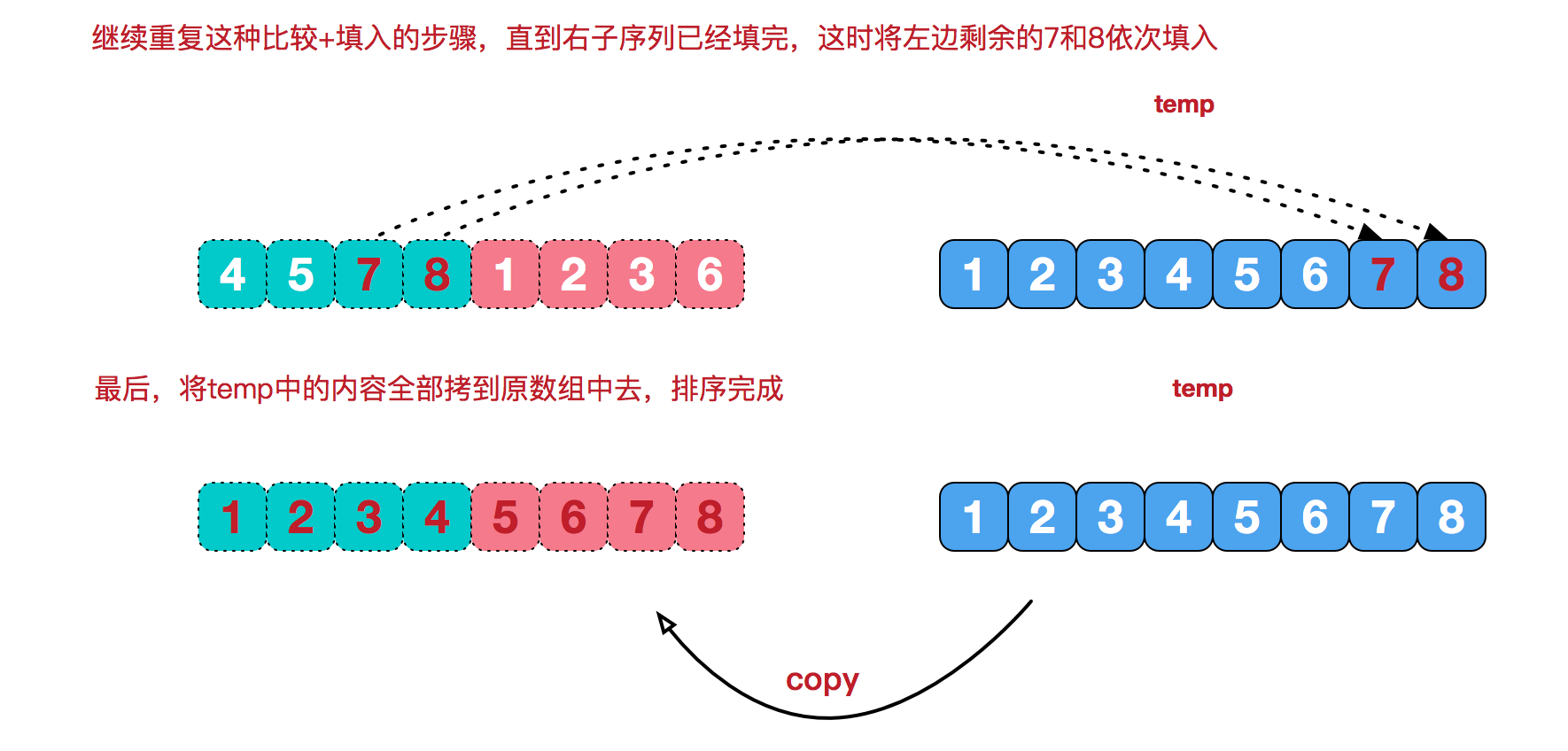
　再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

【算法复杂度】

 

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(nlogn)	O(nlogn)	O(nlogn)	O(n)	稳定

 

【动图演示】

 

【算法实现】

/*
** 归并排序的C++实现
** 假设：对N个数字进行升序排序
*/
void merge(int *data,int start,int end,int *result){
    int llen= (start+end)/2-start+1; // 左部分区间的数据元素的个数
    int lindex = start;
    int rindex = start + llen;
    int poinetr = start;
    while(lindex < start + llen && rindex < end+1){  // 分别对已经排好序的左区间和右区间进行合并
        if(data[lindex] <= data[rindex])
            result[poinetr++] = data[lindex++];
        else
            result[poinetr++] = data[rindex++];
    }
    while(lindex < start + llen)
        result[poinetr++] = data[lindex++];
    while(rindex < end+1)
        result[poinetr++] = data[rindex++];
}

void mergeSort(int *data, int start, int end, int *result){
    if(1 == end - start) {  //如果区间中只有两个元素，则对这两个元素进行排序
        if(data[start] > data[end]){
            data[start] ^= data[end];
            data[end] ^= data[start];
            data[start] ^= data[end];
        }
        return ;
    }
    else if(0 == end - start)   //如果只有一个元素，则不用排序
        return ;
    else{ // 继续划分子区间，分别对左右子区间进行排序
        mergeSort(data,start,(start+end)/2,result);
        mergeSort(data,(start+end)/2+1,end,result);
        merge(data,start,end,result);  // 归并已经排好序的start到end之间的数据
        for(int i = start;i <= end;++i) //把排序后的区间数据复制到原始数据中去
            data[i] = result[i];
    }
}