希尔排序

【基本思想】

　　先取一个小于n的整数d1作为第一个增量，把数组元素分组，所有距离为d1的倍数的记录放在同一个组中，先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量  =1(  <  …<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

 

【算法复杂度】 

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(nlogn)	O(nlog2n)	O(n1.3)	O(1)	不稳定

 

时间复杂度>>>

希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。

 

稳定性>>>

　　由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

 

【动图演示】

 

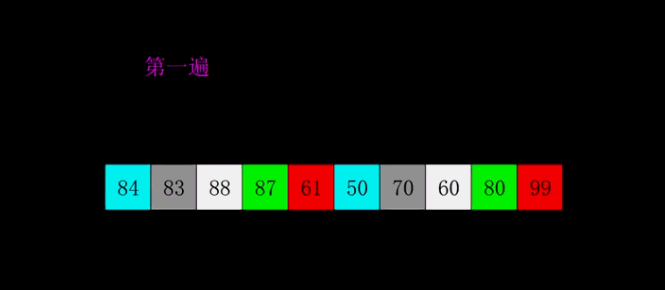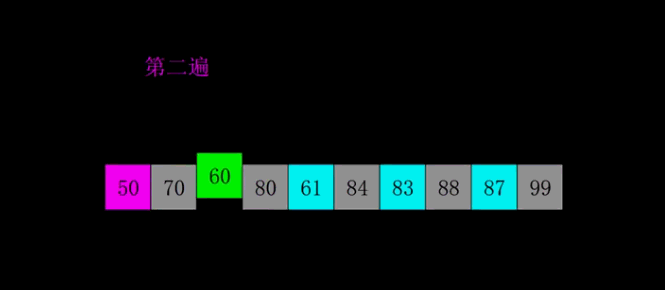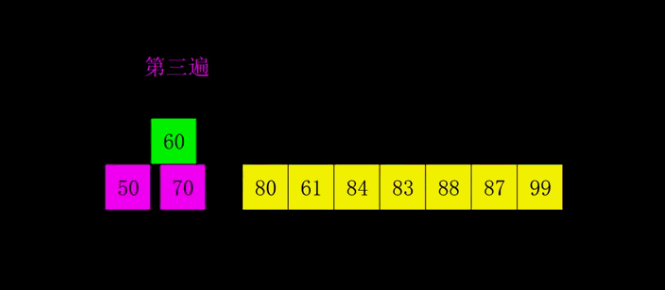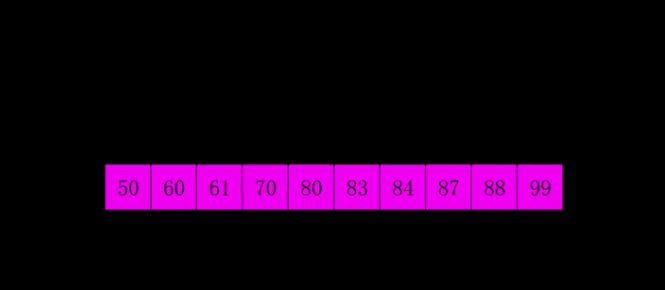
【算法实现】

/*
** 希尔排序的C++实现
** 假设：对N个数字进行升序排序
*/
void shellSort(vector<int>& seq){
    int i,j,temp,increment = seq.size(); 
    do{ 
        increment = increment / 3 + 1; // 缩小增量
        for (i = increment; i < seq.size(); i++){
            if (seq[i] < seq[i - increment]){
                temp = seq[i];
                for (j = i - increment; j >=0  && temp < seq[j]; j -= increment) // 寻找插入位置
                    seq[j + increment] = seq[j];
                seq[j + increment] = temp; // 将数字插入到正确的位置
            }
        }
    }while (increment > 1);
}