有序表查找

折半查找/二分查找

前提：线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须采用顺序存储。

基本思想:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。

 

int Binary_Search(int *a, int n, int key)
{
    int low, high, mid;    /* 定义最低下标为记录首位 */
    low = 1;    /* 定义最高下标为记录末位 */
    high = n;
    while (low <= high)
    {
        mid = (low + high) / 2;    /* 折半 */
        if (key < a[mid])    /* 若查找值比中值小 */
            high = mid - 1;        /* 最高下标调整到中位下标小一位 */
        else if (key > a[mid])    /* 若查找值比中值大 */
            low = mid + 1;    /* 最低下标调整到中位下标大一位 */
        else    /* 若相等则说明mid即为查找到的位置 */
            return mid;
    }
    return 0;
}

 

插值查找

改进后的二分查找

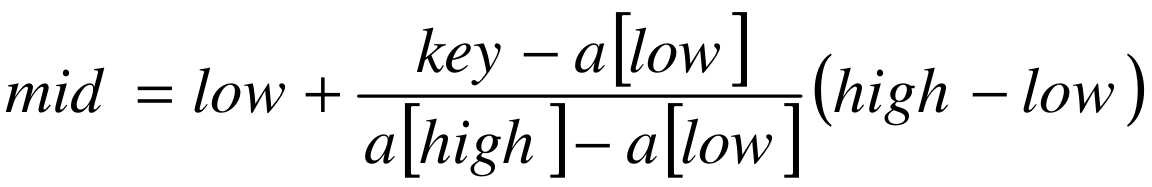
int Binary_Search(int *a, int n, int key)
{
    int low, high, mid;    /* 定义最低下标为记录首位 */
    low = 1;    /* 定义最高下标为记录末位 */
    high = n;
    while (low <= high)
    {
        mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]); /* 插值 */
        if (key < a[mid])    /* 若查找值比中值小 */
            high = mid - 1;        /* 最高下标调整到中位下标小一位 */
        else if (key > a[mid])    /* 若查找值比中值大 */
            low = mid + 1;    /* 最低下标调整到中位下标大一位 */
        else    /* 若相等则说明mid即为查找到的位置 */
            return mid;
    }
    return 0;
}

 

斐波那契查找

斐波那契数列的一条性质：前一个数除以相邻的后一个数，比值无限接近黄金分割。

算法思想：采用最接近查找长度的斐波那契数值来确定拆分点。

举个例子来讲：现有长度为9的数组，要对它进行拆分，对应的斐波那契数列（长度先随便取，只要最大数大于9即可）{1，1，2，3，5，8，13，21，34}，不难发现，大于9且最接近9的斐波那契数值是f[6]=13，为了满足所谓的黄金分割，所以它的第一个拆分点应该就是f[6]的前一个值f[5]=8，即待查找数组array的第8个数，对应到下标就是array[7]，依次类推；推演到一般情况，假设有待查找数组array[n]和斐波那契数组F[k],并且n满足n>=F[k]-1&&n < F[k+1]-1，则它的第一个拆分点middle=F[k]-1。

int Fibonacci_Search(int *a, int n, int key)
{
    int low, high, mid, i, k = 0;
    
    low = 1;    /*定义最低下标为记录首位 */
    high = n;    /*定义最高下标为记录末位 */

    while (n > F[k] - 1)    /* 计算n位于斐波那契数列的位置  数组F为斐波那契数列*/
        k++;

    for (i = n; i < F[k] - 1; i++)        /* 将不满的数值补全 */
        a[i] = a[n];
    
    while (low <= high) 
    {
        mid = low + F[k - 1] - 1;    /* 计算当前分隔的下标 */
        
        if (key < a[mid])    /* 若查找记录小于当前分隔记录 */
        {
            high = mid - 1;    /* 最高下标调整到分隔下标mid-1处 */
            k = k - 1;    /* 斐波那契数列下标减一位 */
        }    
        else if (key > a[mid])    /* 若查找记录大于当前分隔记录 */
        {
            low = mid + 1;    /* 最低下标调整到分隔下标mid+1处 */
            k = k - 2;    /* 斐波那契数列下标减两位 */
        }
        else
        {
            if (mid <= n)    /* 若相等则说明mid即为查找到的位置 */
                return mid;
            else        /* 若mid>n说明是补全数值,返回n */
                return n;
        }
    }
    return 0;
}