DFS(深度优先搜索)

深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。

　　沿着树的深度遍历树的节点，尽可能深的搜索树的分支，当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。   ---《维基百科》

 

时间复杂度：
空间复杂度：

 

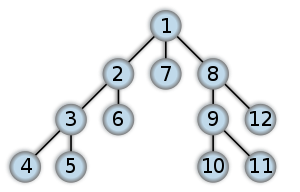
树的DFS： 

 算法实现

1. 首先将根节点压入栈中；
2. 从栈中取出第一个节点，并检验它是否为目标；
3. 如果找到目标，则结束搜寻并回传结果，否则将它的右子结点和左子结点先后压入栈中；
4. 重复步骤2，直到栈为空。

/* 
 * 树的深度优先搜索
 * 省去了初始化树的部分
*/

// 树的结点类型
struct Node {
  int self;     // 结点值
  Node *left;   // 左结点
  Node *right;  // 右结点
};

int target = 5; // 要查找的值
const int TREE_SIZE = 9; // 树的结点个数
std::stack<Node *> unvisited; // 未访问过的树结点指针
Node nodes[TREE_SIZE]; // 树的结点数组
Node *current;  // 当前指向的结点指针

void dfs(){
  unvisited.push(&nodes[0]); // 根节点入栈
  while (!unvisited.empty()) {
    current = unvisited.top();
    unvisited.pop();
    if(current->self==target){
      // do something
      return ;
    }
    if (current->right != NULL)
      unvisited.push(current->right); // 右结点入栈
    if (current->left != NULL)
      unvisited.push(current->left); // 左结点入栈
  }
}

 

 

图的DFS： 

 算法实现

1. 创建一个访问数组，每次访问一个结点时将该结点在访问数组中的值置1；
2. 检验当前结点的值与目标值是否相等，相等则返回，否则，生成下一个结点的坐标；
3. 检验下一个结点的坐标是否符合条件，若符合条件则递归的遍历下一个结点；
4. 重复步骤2、3，直到所有结点遍历完毕。

/*
 * 图的深度优先遍历
 * 图采用邻接矩阵存储
 * locateVex() - 计算顶点的下标
 * createGraph() - 创建图
 * dfs() - 深度优先遍历图
*/

#include <iostream>
#include <stack>
using namespace std;

const int MAXN = 100;
stack<char> q;
bool visited[MAXN];

typedef struct Graph {
    char vexs[MAXN];  //顶点表
    int arcs[MAXN][MAXN]; //邻接矩阵
    int vexnum, arcnum;  //当前的顶点数和边数
} Graph;

int locateVex(Graph &graph, char v) {
    for (int i = 0; i < graph.vexnum; i++)
        if (graph.vexs[i] == v)
            return i;
    return 0;
}

int createGraph(Graph &graph) {
    int i, j, k;
    char v1, v2;
    cout << "please input the number of vertices and the number of edges:" << endl;
    cin >> graph.vexnum >> graph.arcnum;

    // 读入顶点信息
    cout << "please input vertex information:" << endl;
    for (i = 0; i < graph.vexnum; i++)
        cin >> graph.vexs[i];

    // 初始化邻接矩阵边，0表示顶点i和j之间无边
    for (i = 0; i < graph.vexnum; i++)
        for (j = 0; j < graph.vexnum; j++)
            graph.arcs[i][j] = 0;

    // 读入边集信息
    cout << "please input the edge information:" << endl;
    for (k = 0; k < graph.arcnum; k++) {
        cin >> v1 >> v2;
        i = locateVex(graph, v1);    //找到顶点i的下标
        j = locateVex(graph, v2);   //找到顶点j的下标
        graph.arcs[i][j] = graph.arcs[j][i] = 1;
    }
    return 1;
}

void dfs(Graph &graph, char v0) {
    int cur, cur_index;
    int index0 = locateVex(graph, v0);
    visited[index0] = 1;
    q.push(v0);
    
    cout << "the result is:" << endl;
    while (!q.empty()) {
        cur = q.top();    // 
        q.pop();        // 将栈顶头元素出栈
        cur_index = locateVex(graph, cur);  //得到顶点对应下标
        cout << graph.vexs[cur_index] << " ";
        for (int i = 0; i < graph.vexnum; i++) {
            if (graph.arcs[cur_index][i] && !visited[i]) {
                q.push(graph.vexs[i]);  //将顶点入队
                visited[i] = 1;     //顶点已被访问
            }
        }
    }
}

int main()  {
    Graph graph;
    createGraph(graph);
    dfs(graph, 'a');
    return 0;
}