先验概率，后验概率，最大似然估计，最大后验概率

先验概率和后验概率

教科书上的解释总是太绕了。其实举个例子大家就明白这两个东西了。

假设我们出门堵车的可能因素有两个（就是假设而已，别当真）：车辆太多和交通事故。

堵车的概率就是先验概率 。

那么如果我们出门之前我们听到新闻说今天路上出了个交通事故，那么我们想算一下堵车的概率，这个就叫做条件概率 。也就是P(堵车|交通事故)。这是有因求果。

如果我们已经出了门，然后遇到了堵车，那么我们想算一下堵车时由交通事故引起的概率有多大，

那这个就叫做后验概率 （也是条件概率，但是通常习惯这么说）。也就是P(交通事故|堵车)。这是有果求因。

下面的定义摘自百度百科：

先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现.

后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,如贝叶斯公式中的,是"执果寻因"问题中的"因".

那么这两个概念有什么用呢？

最大似然估计

我们来看一个例子。

有一天，有个病人到医院看病。他告诉医生说自己头痛，然后医生根据自己的经验判断出他是感冒了，然后给他开了些药回去吃。

有人肯定要问了，这个例子看起来跟我们要讲的最大似然估计有啥关系啊。

关系可大了，事实上医生在不知不觉中就用到了最大似然估计（虽然有点牵强，但大家就勉为其难地接受吧^_^）。

怎么说呢？

大家知道，头痛的原因有很多种啊，比如感冒，中风，脑溢血...（脑残>_<这个我可不知道会不会头痛，还有那些看到难题就头痛的病人也不在讨论范围啊！）。

那么医生凭什么说那个病人就是感冒呢？哦，医生说这是我从医多年的经验啊。

咱们从概率的角度来研究一下这个问题。

其实医生的大脑是这么工作的，

他计算了一下

P(感冒|头痛)（头痛由感冒引起的概率，下面类似）

P(中风|头痛)

P(脑溢血|头痛)

...

然后这个计算机大脑发现，P(感冒|头痛)是最大的，因此就认为呢，病人是感冒了。看到了吗？这个就叫最大似然估计（Maximum likelihood estimation，MLE） 。

咱们再思考一下，P(感冒|头痛)，P(中风|头痛)，P(脑溢血|头痛)是先验概率还是后验概率呢？

没错，就是后验概率。看到了吧，后验概率可以用来看病（只要你算得出来，呵呵）。

事实上，后验概率起了这样一个用途，根据一些发生的事实（通常是坏的结果），分析结果产生的最可能的原因，然后才能有针对性地去解决问题。

那么先验概率有啥用呢？

我们来思考一下，P(脑残|头痛)是怎么算的。

P(脑残|头痛)=头痛的人中脑残的人数/头痛的人数

头痛的样本倒好找，但是头痛的人中脑残的人数就不好调查了吧。如果你去问一个头痛的人你是不是脑残了，我估计那人会把你拍飞吧。

接下来先验概率就派上用场了。

根据贝叶斯公式 ，

P(B|A)=P(A|B)P(B)/P(A)

我们可以知道

P(脑残|头痛)=P(头痛|脑残)P(脑残)/P(头痛)

注意，(头痛|脑残)是先验概率，那么利用贝叶斯公式我们就可以利用先验概率把后验概率算出来了。

P(头痛|脑残)=脑残的人中头痛的人数/脑残的人数

这样只需要我们去问脑残的人你头痛吗，明显很安全了。

（你说脑残的人数怎么来的啊，那我们就假设我们手上有一份传说中的脑残名单吧。那份同学不要吵，我没说你在名单上啊。

再说调查脑残人数的话咱就没必要抓着一个头痛的人问了。起码问一个心情好的人是否脑残比问一个头痛的人安全得多）

我承认上面的例子很牵强，不过主要是为了表达一个意思。后验概率在实际中一般是很难直接计算出来的，相反先验概率就容易多了。因此一般会利用先验概率来计算后验概率。

似然函数与最大似然估计

下面给出似然函数跟最大似然估计的定义。

我们假设f是一个概率密度函数，那么

$x/mapsto f(x/mid/theta), /!$

是一个条件概率密度函数（θ 是固定的）

而反过来，

$/theta/mapsto f(x/mid/theta), /!$

叫做似然函数 （x是固定的）。

一般把似然函数写成

$L(/theta /mid x)=f(x/mid/theta), /!$

θ是因变量。

而最大似然估计 就是求在θ的定义域中，当似然函数取得最大值时θ的大小。

意思就是呢，当后验概率最大时θ的大小。也就是说要求最有可能的原因。

由于对数函数不会改变大小关系，有时候会将似然函数求一下对数，方便计算。

例子：

我们假设有三种硬币，他们扔到正面的概率分别是1/3，1/2，2/3。我们手上有一个硬币，但是我们并不知道这是哪一种。因此我们做了一下实验，我们扔了80次，有49次正面，31次背面。那么这个硬币最可能是哪种呢？我们动手来算一下。这里θ的定义域是{1/3，1/2，2/3}

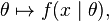
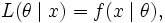
$/begin{align}/Pr(/mathrm{H} = 49 /mid p=1/3) & = /binom{80}{49}(1/3)^{49}(1-1/3)^{31} /approx 0.000 //[6pt]/Pr(/mathrm{H} = 49 /mid p=1/2) & = /binom{80}{49}(1/2)^{49}(1-1/2)^{31} /approx 0.012 //[6pt]/Pr(/mathrm{H} = 49 /mid p=2/3) & = /binom{80}{49}(2/3)^{49}(1-2/3)^{31} /approx 0.054./end{align}$

当p=2/3时，似然函数的值最大，因此呢，这个硬币很可能是2/3。

最大后验概率：

最大后验估计运用了贝叶斯估计的思想，但是它并不去求解 $p(\theta|\mathcal{D})$ ，而是直接获得 $\theta_{B}^{*}$ 。从贝叶斯估计的公式可以看出， $Z_D$ 是与 $\theta$ 无关的，要求得使 $p(\theta|\mathcal{D})$ 最的的 $\theta$ ，等价于求解下面的式子：