dls的数据结构-笛卡尔树，st表，带权并查集

笛卡尔树

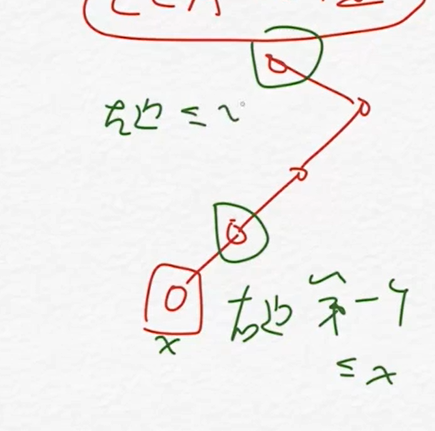
每次将序列中最小的数当成根，递归左右，对跟左边和右边递归地建树
最大的也是类似的
性质： 
区间最小值：两个端点的lca的值
笛卡尔树的中序遍历是原数组(对一般的二叉搜索树都是成立的)
一个点，一路向上都是父亲的左儿子，然后再是一个的父亲的右儿子，
第一个左儿子是右边第一个大于等于他的，第一个左拐的左边第一个小于等于他的
或者可以想想成，一个点的祖先都比他的子孙要小，左右儿子关系，实际是数组中的相对位置关系
建树：最左边的链维护一个单调栈

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e6+10;

int ans[N], tot;



// a存放原序列，top从0开始，右边闭区间
// 建立区间最小值笛卡尔树
// 根节点是stk[1]
int stk[N], top, a[N], l[N], r[N];
int n;

void dfs(int u){
	ans[u] = ++tot;
	if(l[u]) dfs(l[u]);
	if(r[u]) dfs(r[u]);
}
void build(){
	int top = 0;
	for(int i = 1; i <= n; i ++) l[i] = r[i] = 0;
	for(int i = 1; i <= n; i ++){
		int k = top;
		while(k > 0 && a[stk[k]] > a[i] ) k--;
		if(k) r[stk[k]] = i;
		if(k < top) l[i] = stk[k + 1];
		stk[++k] = i;
		top = k; 
	}
	// 把树建出来
	// for(int i = 1; i <= n; i ++){
	// 	if(l[i]) add(i, l[i]);
	// 	if(r[i]) add(i, r[i]);
	// }
	dfs(stk[1]);
}

int main(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
	build();
	for(int  i = 1; i <= n; i ++) printf("%d ", ans[i]);
	puts("");
 	return 0;
}

#include<bits/stdc++.h>

using namespace std;
const int N = 1e6+10;
const int LOGN = 21;


int n, q;
long long val[N], f[22][N];
void init(){
    // 这里注意val可能存在的边界问题
    for(int i = 1; i <= n; i ++) f[0][i] = val[i];
    for(int i = 1; i < LOGN; i ++){
        for(int j = 1; j + (1 << (i - 1)) <= n; j ++){
            f[i][j] = max(f[i - 1][j + (1 << (i - 1))], f[i - 1][j]);
        }
    }
}

unsigned int A, B, C;
inline unsigned int rng61() {
    A ^= A << 16;
    A ^= A >> 5;
    A ^= A << 1;
    unsigned int t = A;
    A = B;
    B = C;
    C ^= t ^ A;
    return C;
}

int main(){
	scanf("%d%d%u%u%u", &n, &q, &A, &B, &C);
	for(int i = 1; i <= n; i ++) val[i] = rng61();
	init();
	long long res = 0;
	while(q --){
		int l =  rng61() % n + 1, r = rng61() % n + 1;
		if(l > r) swap(l, r);
		int len = __lg(r - l + 1);
		res ^= max(f[len][l], f[len][r - (1 << len) + 1]);
	}
	cout << res << endl;
}

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 2e5+10;
int p[N];
LL d[N];

int find(int x){
	if(x != p[x]){
		int t = find(p[x]);
		d[x] += d[p[x]];
		p[x] = t;
	}
	return p[x];
}

int main(){
	int n, q; scanf("%d %d", &n, &q);
	for(int i = 1; i <= n; i ++) p[i] = i;
	LL t = 0;
	while(q --){
		int op; scanf("%d", &op);
		if(op == 1){
			int l, r, x; scanf("%d %d %d", &l, &r, &x);
			l = (l + t) % n + 1;
			r = (r + t) % n + 1;
			int pl = find(l), pr = find(r);
			if(pl != pr){
				p[pl] = pr;
				d[pl] = x + d[r] - d[l];
			}
		}
		else if(op == 2){
			int l, r; scanf("%d %d", &l, &r);
			l = (l + t) % n + 1;
			r = (r + t) % n + 1;
			int pl = find(l), pr = find(r);
			if(pl == pr){
				printf("%lld\n", d[l] - d[r]);
				t = abs(d[l] - d[r]);
			}
		}
	}
	return 0;
}