
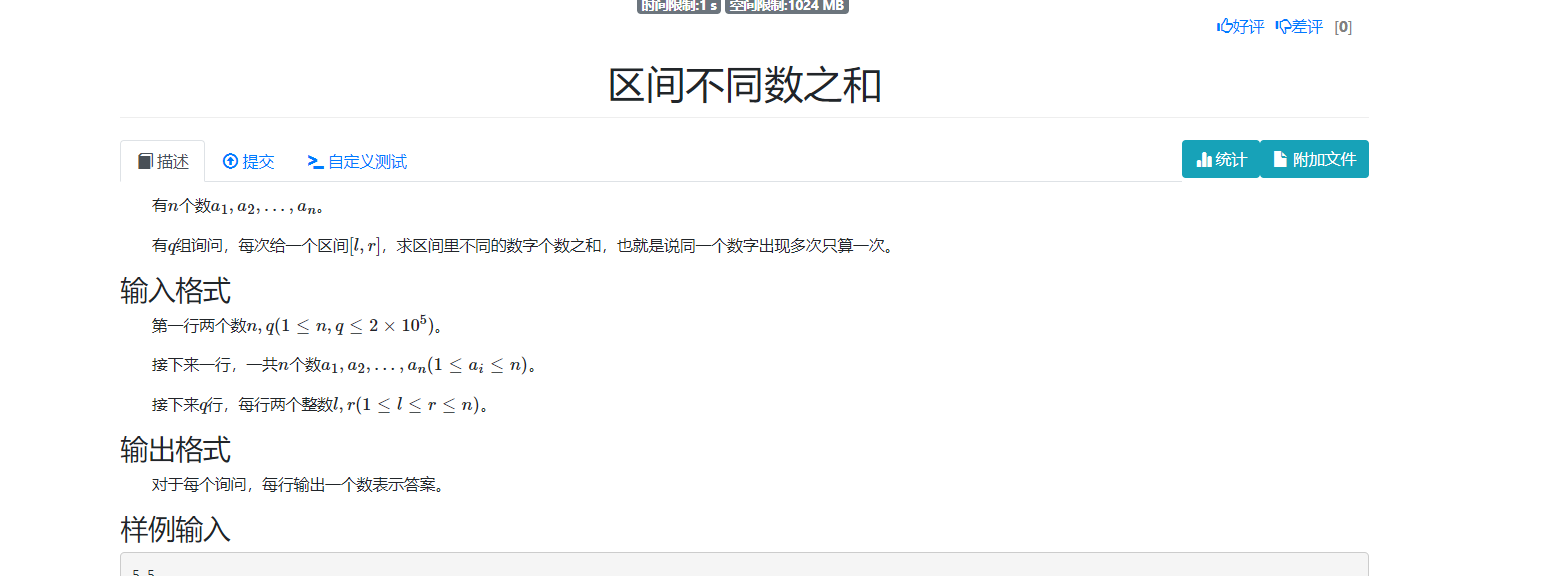
二维数点
1. 两条限制,x1=<x<=x2, y1=<y<=y2, 我们可以将其转化成单边界的问题
2. 对于上面类似的问题都可以转换成扫描线的形式,在该题中扫y,对x进行计数
3. 也有离线的思想
4. 事件的思想
5. vx离散化只需要离散点的x就行了,其他的不需要离散,其中lowber_bound + 1求第一个==的坐标,upper_bound求最后一个<=他的坐标
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5+10;
vector<array<int, 4>> events;
vector<int> vx;
int res[N];
LL tr[N];
int m;
int lowbit(int x){
return x & (-x);
}
int modify(int x, LL v){
for(int i = x; i <= m; i += lowbit(i)) tr[i] += v;
}
LL query(int x){
LL sum = 0;
for(int i = x; i; i -= lowbit(i)) sum += tr[i];
return sum;
}
int main(){
int n, q; scanf("%d %d", &n, &q);
for(int i = 1; i <= n; i ++){
int x, y; scanf("%d %d", &x, &y);
events.push_back({y, 0, x});
vx.push_back(x);
}
for(int i = 1; i <= q; i ++){
int x1, y1, x2, y2; scanf("%d %d %d %d", &x1, &x2, &y1, &y2);
events.push_back({y2, 1, x2, i});
events.push_back({y1 - 1, 1, x1 - 1, i});
events.push_back({y1 - 1, 2, x2, i});
events.push_back({y2, 2, x1 - 1, i});
}
sort(events.begin(), events.end());
sort(vx.begin(), vx.end());
vx.erase(unique(vx.begin(), vx.end()), vx.end());
m = vx.size() ;
for(auto evt : events){
if(evt[1] == 0){
int x = lower_bound(vx.begin(), vx.end(), evt[2] ) - vx.begin() + 1;
modify(x, 1);
}
else{
int x = upper_bound(vx.begin(), vx.end(), evt[2]) - vx.begin();
res[evt[3]] += (evt[1] == 1) ? query(x) : -1 * query(x);
}
}
for(int i = 1; i <= q; i ++){
printf("%d\n", res[i]);
}
return 0;
}
1.维护pos[i], 表示i上一次出现的位置,
2.对r进行离线遍历,维护ans[l]的答案,ans[l]表示前面l-r的结果,就可以发现需要加ans区间就是pos[a[i]]-i这部分,
3.离线访问的存储
或者可以转化成扫描线的问题求解的是pos[a[i]]<l, l<=a[i]<=r的问题,也是两个约束
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5+10;
vector<array<int, 2>> que[N];
LL res[N];
LL tr[N];
int a[N], n, pos[N];
int lowbit(int x){
return x & (-x);
}
int modify(int x, LL v){
for(int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}
LL query(int x){
LL sum = 0;
for(int i = x; i; i -= lowbit(i)) sum += tr[i];
return sum;
}
int main(){
int q; scanf("%d %d", &n, &q);
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for(int i = 1; i <= q; i ++){
int l, r; scanf("%d %d", &l, &r);
que[r].push_back({l, i});
}
for(int r = 1; r <= n; r ++){
int p = pos[a[r]];
pos[a[r]] = r;
modify(p + 1, a[r]);
modify(r + 1, -a[r]);
for(auto qu : que[r]){
res[qu[1]] = query(qu[0]);
}
}
for(int i = 1; i <= q; i ++){
printf("%lld\n", res[i]);
}
return 0;
}
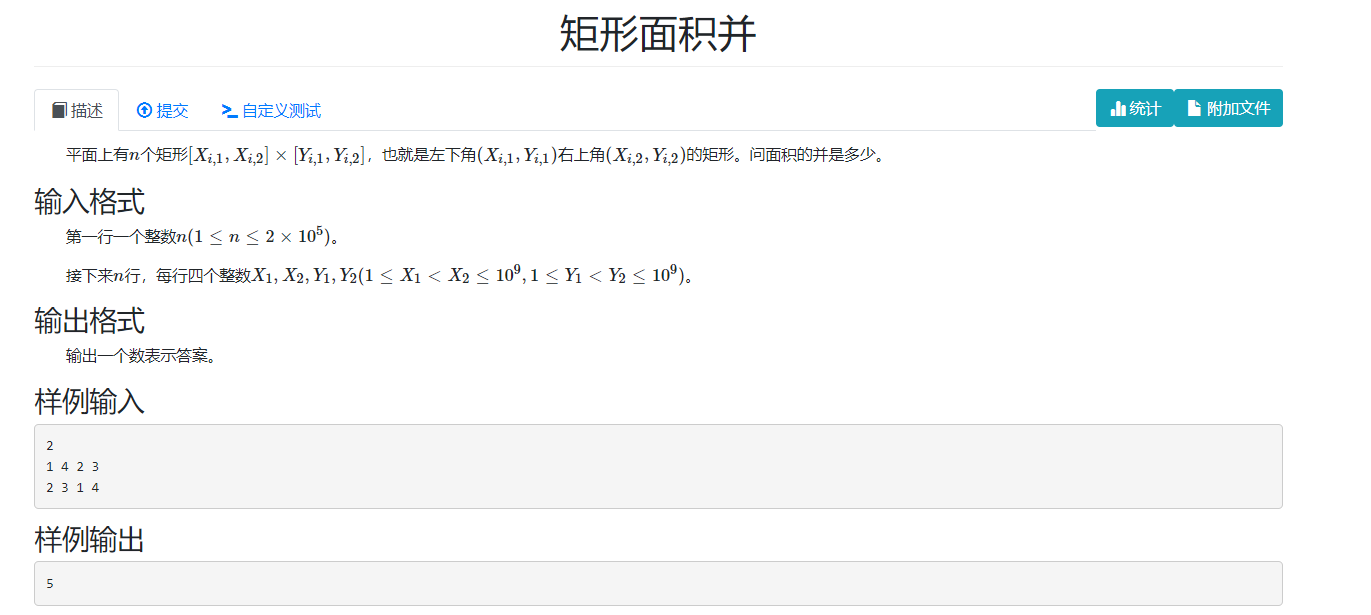
1. 线段树维护区间的最小值,和最小值出现的区间长度总和(离散化后的总长度是在build中体现的)
2. 那么被覆盖的区间就是总长度-0的长度
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5+10;
vector< array<int, 4> > events;
vector< int > vx;
int w[N];
struct node{
int l, r;
LL minn, minncnt;
LL add;
}tr[8*N];
void pushup(node &F, node &L, node &R){
F.minn = min(F.minn, R.minn);
F.minncnt = 0;
if(F.minn == L.minn) F.minncnt += L.minncnt;
if(F.minn == R.minn) F.minncnt += R.minncnt;
}
void pushup(int u){
pushup(tr[u], tr[u<<1], tr[u<<1|1]);
}
void pushdown(node &F, node &L, node &R){
L.add += F.add;
R.add += F.add;
L.minn += F.add;
R.minn += F.add;
F.add = 0;
}
void pushdown(int u){
pushdown(tr[u], tr[u<<1], tr[u<<1|1]);
}
void build(int u, int l, int r){
if(l == r){
tr[u] = {l, r, 0, vx[r] - vx[r-1], 0};
}
else{
tr[u] = {l, r, 0, 0, 0};
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int v){
if(tr[u].l >= l && tr[u].r <= r) {
tr[u].add += v;
tr[u].minn += v;
}
else{
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u<<1, l, r, v);
if(r > mid) modify(u<<1|1, l, r, v);
pushup(u);
}
}
int main(){
int n; scanf("%d", &n);
for(int i = 1; i <= n; i ++){
int x1, x2, y1, y2; scanf("%d %d %d %d", &x1, &x2, &y1, &y2);
events.push_back({y1, 1, x1, x2});
events.push_back({y2, -1, x1, x2});
vx.push_back(x1);
vx.push_back(x2);
}
sort(events.begin(), events.end());
sort(vx.begin(), vx.end());
vx.erase(unique(vx.begin(), vx.end()), vx.end());
build(1, 1, vx.size() - 1);
LL ans = 0; int prey = 0;
int totlen = tr[1].minncnt;
for(auto evt : events){
int tot = totlen;
if(tr[1].minn == 0) tot -= tr[1].minncnt;
// cout << tot << endl;
ans += (LL)(evt[0] - prey) * tot;
prey = evt[0];
// 这里用点来存放线段
int x1 = lower_bound(vx.begin(), vx.end(), evt[2]) - vx.begin() + 1;
int x2 = lower_bound(vx.begin(), vx.end(), evt[3]) - vx.begin();
modify(1, x1, x2, evt[1]);
// cout << x1 << ' ' << x2 << endl;
// cout << evt[0] << ' ' << evt[1] << ' ' << evt[2] << ' ' << evt[3] << ' ' << ans << endl;
}
cout << ans << endl;
return 0;
}
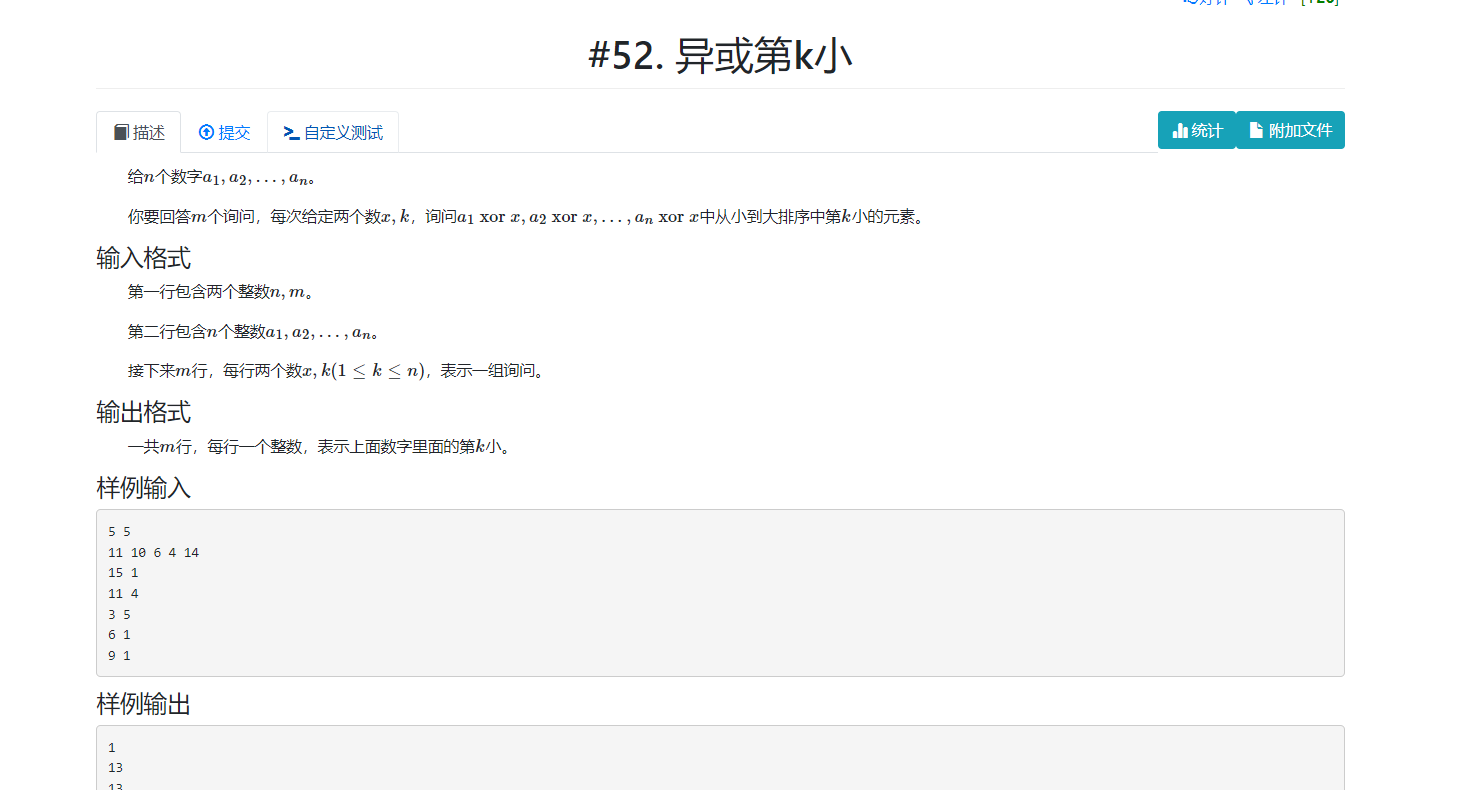
1.相比较普通字典树,多记录一个size就可以了,表示这个节点的子树有多少个结尾的
2. 查询类似于线段树上的二分
3. 题目也可以改成动态修改,动态查询
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5+10, M = 31;
struct Node{
int son[2];
int Size;
}tr[N*M];
int root, tot;
void insert(int x){
int p = root;
for(int i = 30; i >= 0; i --){
int t = x >> i & 1;
tr[p].Size ++;
if(!tr[p].son[t]) tr[p].son[t] = ++ tot;
p = tr[p].son[t];
}
tr[p].Size ++;
}
int serach(int x, int k){
int p = root;
int ans = 0;
for(int i = 30; i >= 0; i --){
int t = x >> i & 1;
if(tr[tr[p].son[t]].Size >= k) p = tr[p].son[t];
else k -= tr[tr[p].son[t]].Size, p = tr[p].son[t ^ 1], ans |= (1 << i);
}
return ans;
}
int main(){
int n, m; scanf("%d %d", &n, &m);
root = ++tot;
for(int i = 1; i <= n; i ++){
int x; scanf("%d", &x);
insert(x);
}
for(int i = 1; i <= m; i ++){
int x, k; scanf("%d %d", &x, &k);
printf("%d\n", serach(x, k));
}
return 0;
}
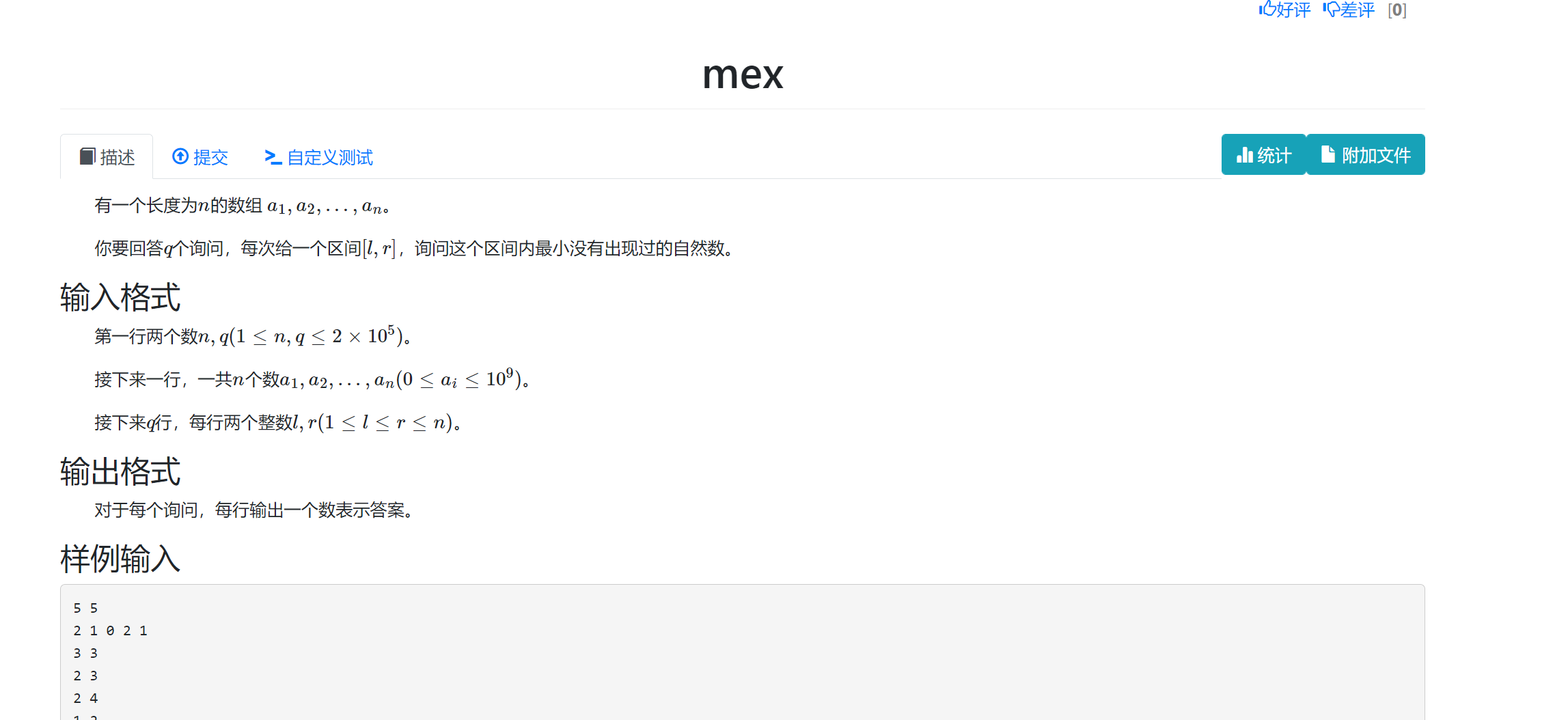
1.权值的位置存放当前遍历到的最后一次出现在哪里
2.线段树维护最小值
3.问题可以转化成求最小的x使得pos[x]<l
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5+10;
vector< pair<int, int> > events[N];
int a[N], res[N];
struct node{
int l, r;
int pos;
}tr[4*N];
void pushup(int u){
tr[u].pos = min(tr[u<<1].pos, tr[u<<1|1].pos);
}
void build(int u, int l, int r){
if(l == r){
tr[u] = {l, r, 0};
}
else{
tr[u] = {l, r, 0};
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
}
void modify(int u, int x, int v){
if(tr[u].l == x && tr[u].r == x) tr[u].pos = v;
else{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u<<1, x, v);
else modify(u<<1|1, x, v);
pushup(u);
}
}
int query(int u, int l){
while(tr[u].l != tr[u].r){
if(tr[u<<1].pos < l) u = u << 1;
else u = u << 1 | 1;
}
return tr[u].l;
}
int main(){
int n, q; scanf("%d %d", &n, &q);
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]), a[i] = min(a[i], n + 1);
for(int i = 1; i <= q; i++){
int l, r; scanf("%d %d", &l, &r);
events[r].push_back({l, i});
}
build(1, 0, n + 1);
for(int r = 1; r <= n; r ++){
modify(1, a[r], r);
for(auto evt : events[r]){
res[evt.second] = query(1, evt.first);
}
}
for(int i = 1; i <= q; i ++){
printf("%d ", res[i]);
}
puts("");
return 0;
}







