dls的数论-Lucas定理及扩展

Lucas定理

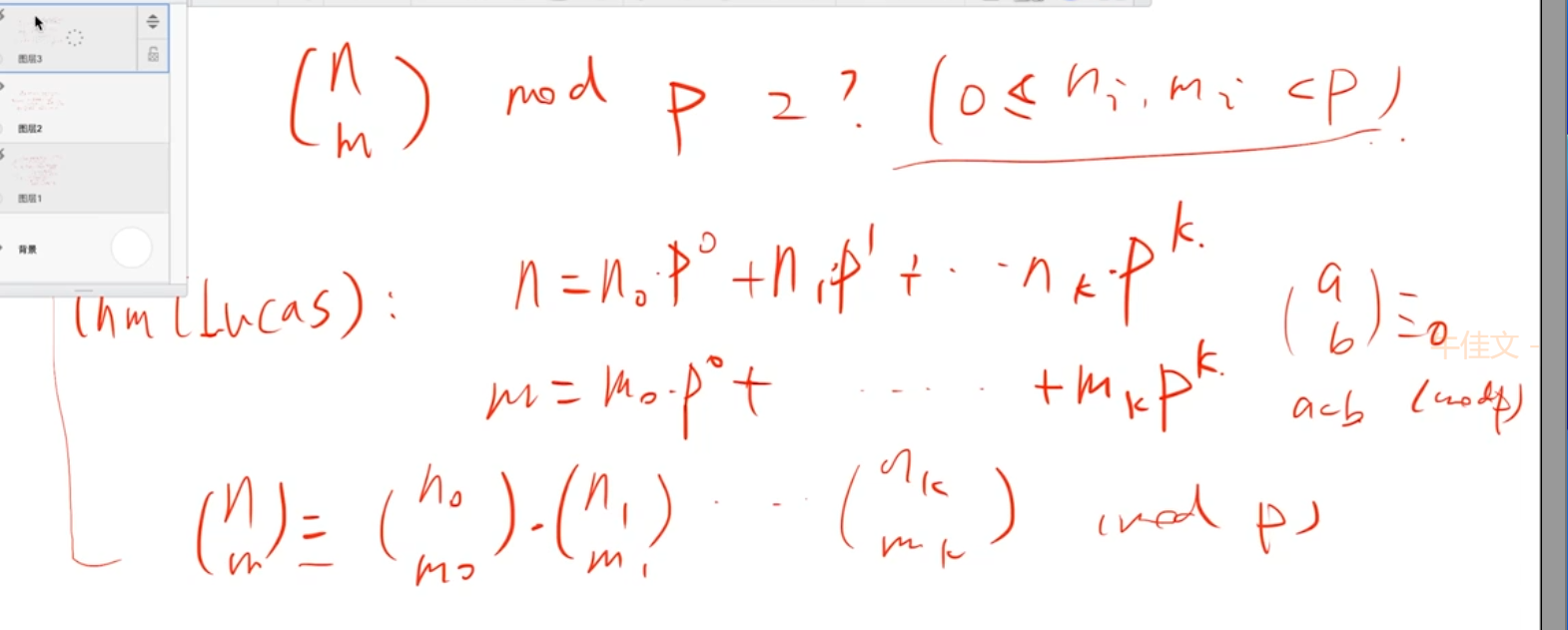
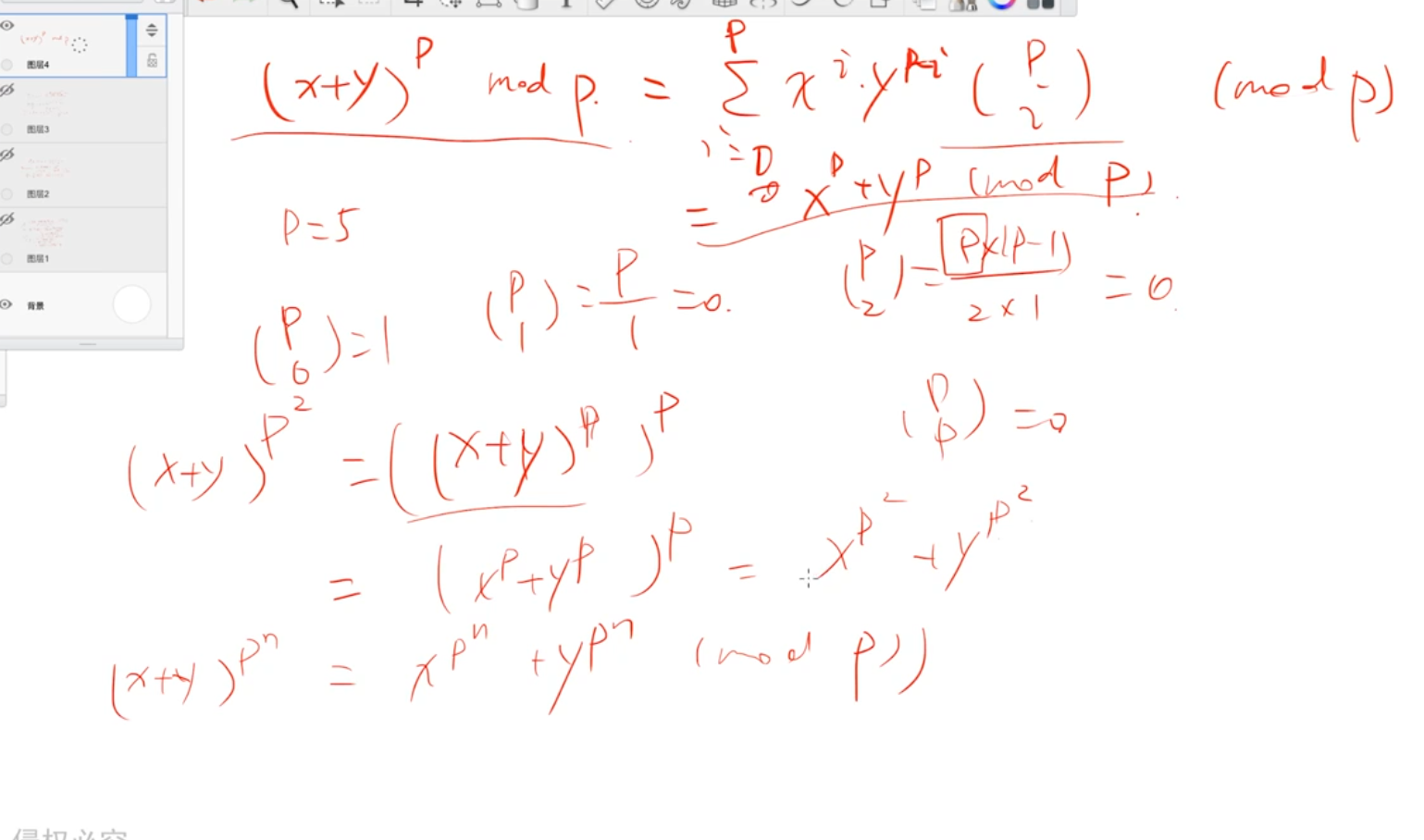
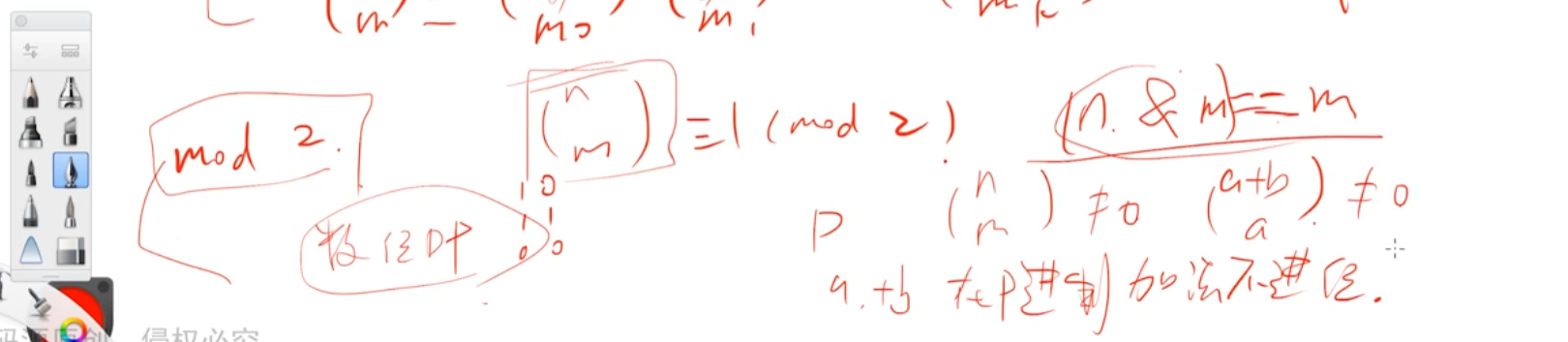
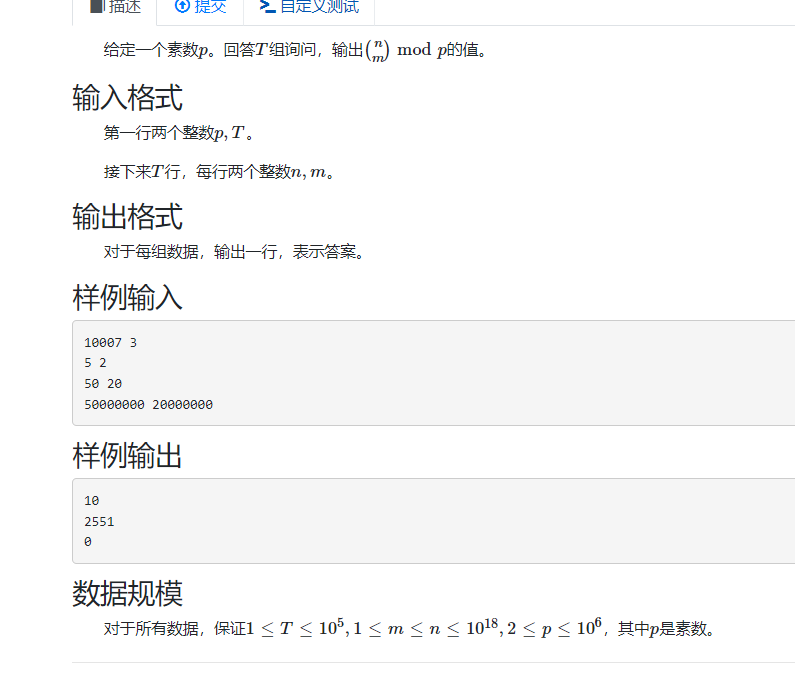
#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e6+10;
int fac[N], inv[N];
LL p, T;
LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

LL C(LL a, LL b){
    if(b < 0 || b > a) return 0;
    return (LL)fac[a] * inv[b] % p * inv[a - b] % p;
}

int main(){
    scanf("%lld%lld", &p, &T);
    fac[0] = 1;
    for(int i = 1; i <= p - 1; i ++) fac[i] = (LL)fac[i - 1] * i % p;
    inv[p - 1] = qmi(fac[p - 1], p - 2, p);
    for(int i = p - 2; i >= 0; i --) inv[i] = (LL)inv[i + 1] * (i + 1) % p;
    while(T--){
        LL n, m; scanf("%lld%lld", &n, &m);
        LL ans = 1;
        while( n > 0 || m > 0){
            ans = ans * C(n % p, m % p) % p;
            n /= p; m /= p;
        }
        printf("%lld\n", ans);
    }    
    return 0;
}

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e6+10;
typedef pair<int, int> PII;
PII pq[N];
LL A[N], B[N], ans[N];
int fac[N], phipe, pr[N];

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

LL cntp, cnts;
LL calc(LL a, LL p, LL pe, int w){
    LL val = 1;
    while(a){
        cntp += a / p * w;
        cnts += a / pe * w;
        val = val * fac[a % pe] % pe;
        a /= p;
    }
    return val;
}

LL C(LL a, LL b, LL p, LL pe){
    cntp = 0, cnts = 0;
    auto f1 = calc(a, p, pe, 1);
    auto f2 = calc(b, p, pe, -1);
    auto f3 = calc(a - b, p, pe, -1);
    LL v1 = f1 * qmi(f2 * f3 % pe, phipe - 1, pe) % pe;
    LL v2 = qmi(p, cntp, pe);
    LL v3 = qmi(fac[pe], cnts, pe);
    return v1 * v2 % pe * v3 % pe; 
}

int main(){
    int q, T;
    scanf("%d %d", &q, &T);
    
    int M = q, t = 0;
    for(int i = 2; i <= q; i ++){
        if(q % i == 0){
            int pe = 1;
            while(q % i == 0) q /= i, pe *= i;
            pq[t ++] = {i, pe}; 
        }
    }
 
    for(int i = 0; i < t; i ++){
        int pe = pq[i].second;
        for(int j = 0; j < M; j ++){
            if(j % pe == 1 && j % (M / pe) == 0){
                pr[i] = j;
                break;
            }
        }
    }

    for(int i = 0; i < T; i ++) scanf("%lld %lld", &A[i], &B[i]);

    for(int i = 0; i < t; i ++){
        int p = pq[i].first, pe = pq[i].second;
        fac[0] = 1;
        for(int j = 1; j <= pe; j ++){
            if(j % p == 0) fac[j] = fac[j - 1];
            else fac[j] = (LL)fac[j - 1] * j % pe;
        }
        phipe = (LL)pe * (p - 1) / p;

        for(int j = 0; j < T; j ++){
            ans[j] = (ans[j] + C(A[j], B[j], p, pe) * pr[i] % M) % M;
        }
    }

    for(int j = 0; j < T; j ++) printf("%lld\n", ans[j]);

    return 0;
}

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n, G, pr[N];
PII pq[N];
int A[N], B[N], fac[N], phipe;
LL ans;

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

LL cntp, cnts;
LL calc(LL a, LL p, LL pe, int w){
    LL val = 1;
    while(a){
        cntp += a / p * w;
        cnts += a / pe * w;
        val = val * fac[a % pe] % pe;
        a /= p;
    }
    return val;
}

LL C(LL a, LL b, LL p, LL pe){
    cntp = 0, cnts = 0;
    LL f1 = calc(a, p, pe, 1);
    LL f2 = calc(b, p, pe, -1);
    LL f3 = calc(a - b, p, pe, -1);
    LL v1 = f1 * qmi(f2 * f3 % pe, phipe - 1, pe) % pe;
    LL v2 = qmi(p, cntp, pe);
    LL v3 = qmi(fac[pe], cnts, pe);
    return v1 * v2 % pe * v3 % pe;
}

int main(){
    scanf("%d %d", &n, &G);
    if(G % 999911659 == 0){
        puts("0");
        return 0;
    }
    int M = 999911659 - 1, t = 0;
    int m = M;
    for(int i = 2; i <= m; i ++){
        if(m % i == 0){
            int pe = 1;
            while(m % i == 0) m /= i, pe *= i;
            pq[t ++] = {i, pe};
        }
    }

    for(int i = 0; i < t; i ++){
        int pe = pq[i].second;
        int Mi = M / pe;
        for(int j = 0; j < M; j += Mi){
            if(j % pe == 1){
                pr[i] = j; break;
            }
        }
    }

    int T = 0;
    for(int i = 1; i <= n / i; i ++){
        if(n % i == 0){
            A[T] = n, B[T ++] = i;
            if(n / i != i) A[T] = n, B[T ++] = n / i;
        }
    }

    for(int i = 0; i < t; i ++){
        int p = pq[i].first, pe = pq[i].second;
        fac[0] = 1;
        for(int j = 1; j <= pe; j ++){
            if(j % p == 0) fac[j] = fac[j - 1];
            else fac[j] = (LL) fac[j - 1] * j % pe;
        }
        phipe = (LL)pe * (p - 1) / p;
        for(int j = 0; j < T; j ++){
            ans = ( ans + (LL)C(A[j], B[j], p, pe) * pr[i] % M ) % M;
        }
    }
    printf("%lld\n", qmi(G, ans, 999911659));

    return 0;
}

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6+10;
int n, G, pr[N];
PII pq[N];
int fac[N], phipe;
PII A[N];
int T;
LL ans;

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

LL cntp, cnts;
LL calc(LL a, LL p, LL pe, int w){
    LL val = 1;
    while(a){
        cntp += a / p * w;
        cnts += a / pe * w;
        val = val * fac[a % pe] % pe;
        a /= p;
    }
    return val;
}

LL C(LL p, LL pe){
    cntp = 0, cnts = 0;
    LL v1 = 1;
    for(int i = 0; i < T; i ++){
        LL f = calc(A[i].first, p, pe, A[i].second);
        v1 = v1 * qmi(f, phipe + A[i].second, pe) % pe;
    }
    LL v2 = qmi(p, cntp, pe);
    LL v3 = qmi(fac[pe],  cnts, pe);
    return v1 * v2 % pe * v3 % pe;
}

int main(){
    int m; scanf("%d", &m);
    int M = m;
    int t = 0;
    for(int i = 2; i <= m; i ++){
        if(m % i == 0){
            int pe = 1;
            while(m % i == 0) m /= i, pe *= i;
            pq[t ++] = {i, pe};
        }
    }

    for(int i = 0; i < t; i ++){
        int pe = pq[i].second;
        int Mi = M / pe;
        for(int j = 0; j < M; j += Mi){
            if(j % pe == 1){
                pr[i] = j; break;
            }
        }
    }

    
    int s, cnt2; scanf("%d %d", &s, &T);
    T ++; A[0] = {s, 1};
    for(int i = 1; i < T; i ++){
        int a; scanf("%d", &a);
        A[i] = {a, -1};
        s -= a;
    }
    if(s < 0){
        puts("Impossible");
        return 0;
    }
    if(s > 0) A[T ++] = {s, -1};

    for(int i = 0; i < t; i ++){
        int p = pq[i].first, pe = pq[i].second;
        fac[0] = 1;
        for(int j = 1; j <= pe; j ++){
            if(j % p == 0) fac[j] = fac[j - 1];
            else fac[j] = (LL) fac[j - 1] * j % pe;
        }
        phipe = (LL)pe * (p - 1) / p;
        ans += C(p, pe) * pr[i];
        ans %= M;
    }
    printf("%lld\n", ans);

    return 0;
}