二分图问题
二分图
1. 充要条件：至少两个顶点并且不存在奇数环
并查集就可以，其实也就是维护两个类别，当有边的时候，说明他两个不是一类的
1. 构造一个二分图进行染色就可以了
2. 情侣之间连边，1-2，3-4，...这样子连边，这样子一定是不存在奇数环的，
3. 这样的话一个人连接的两条边就是一个旁边的人，一个是他的情侣，如果成环的话
说明这个环中每个人都是两条边，所以每个人的对象是都在里面的，所以是k对情侣，所以是偶数条边
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 8e5 + 10;
int h[N], ne[N], e[N], idx;
int color[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
struct Node{
int x, y;
}nodes[N];
void dfs(int u, int c){
color[u] = c;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(!color[j]) dfs(j, 3 - c);
}
}
int main(){
// 记得链接的都是双向边
int n; scanf("%d", &n);
for(int i = 1; i <= 2 * n; i ++) h[i] = -1;
for(int i = 1; i <= n; i ++){
int a, b; scanf("%d %d", &a, &b);
nodes[i] = {a, b};
add(a, b); add(b, a);
}
for(int i = 1; i <= 2 * n; i += 2) add(i, i + 1), add(i + 1, i);
for(int i = 1; i <= 2 * n; i ++){
if(!color[i]) dfs(i, 1);
}
for(int i = 1; i <= n; i ++){
printf("%d %d\n", color[nodes[i].x], color[nodes[i].y]);
}
return 0;
}
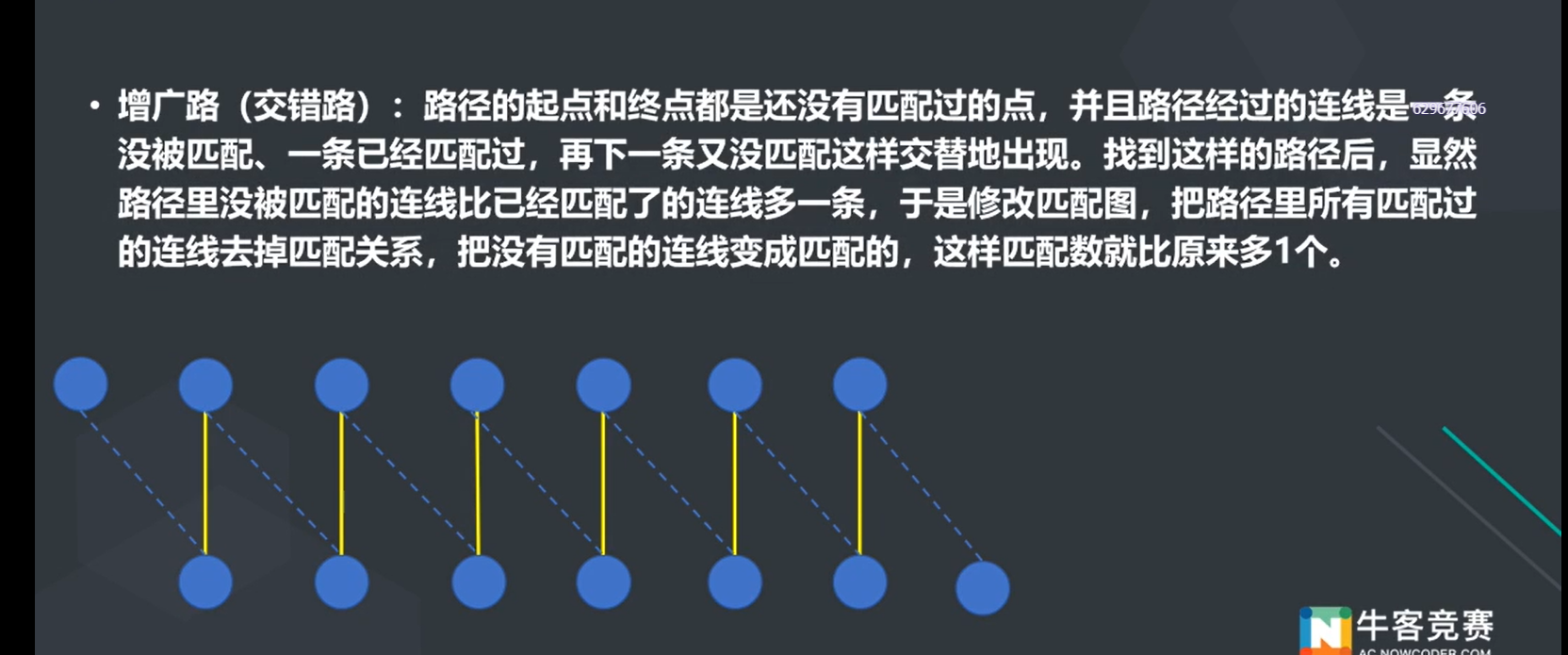
无向图二分图
1. 时间复杂度 邻接表：O(nm)，邻接矩阵：O(n^3)
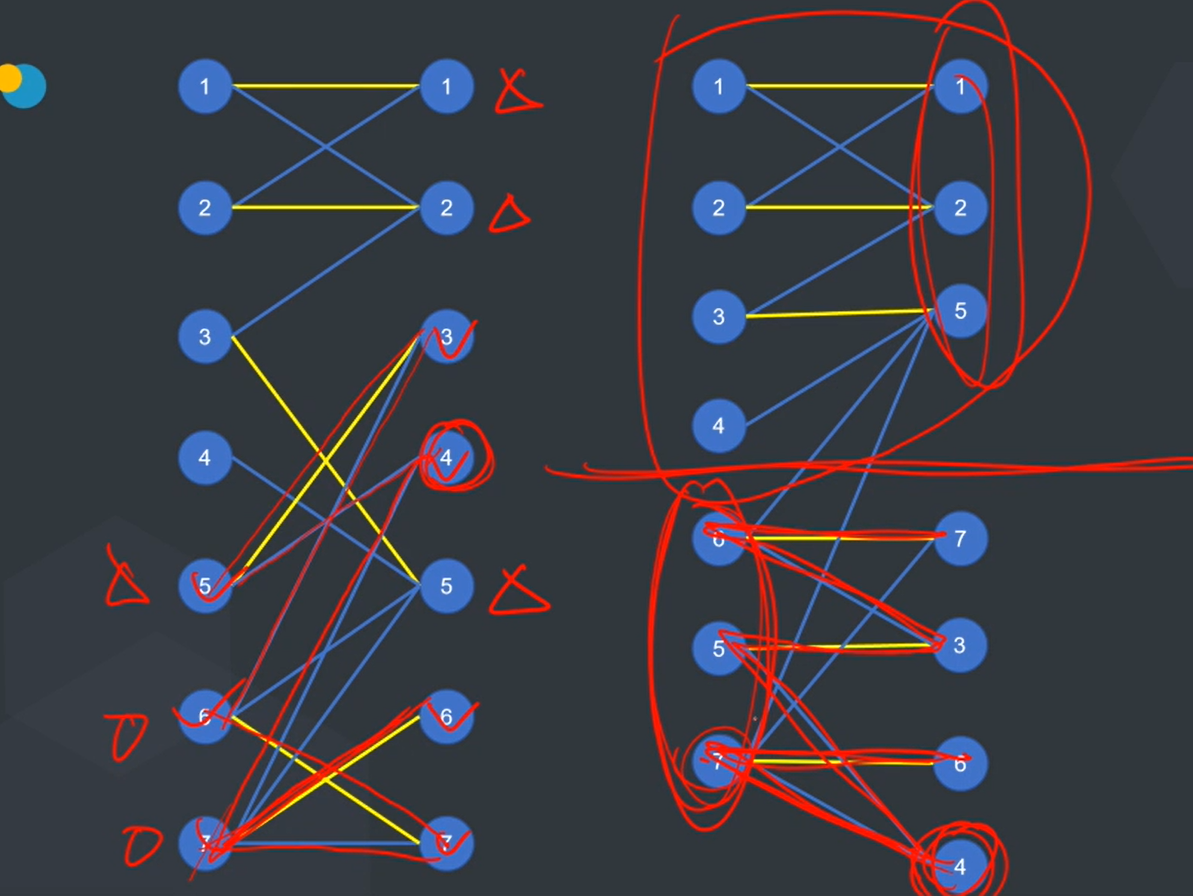
二分图最优匹配 带权的二分图匹配 KM算法
看一下板子，分析二分图的构造
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 55;
int n;
int stu[N], home[N];
int match[N], vis[N];
int h[N], e[N*N], ne[N*N], idx;
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u){
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(vis[j]) continue;
vis[j] = 1;
if(match[j] == -1 || find(match[j])){
match[j] = u;
return true;
}
}
return false;
}
int main(){
int T; cin >> T;
while(T--){
int n; scanf("%d", &n);
for(int i = 1; i <= n; i ++) h[i] = -1; idx = 0;
for(int i = 1; i <= n; i ++) scanf("%d", &stu[i]);
for(int i = 1; i <= n; i ++) scanf("%d", &home[i]);
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= n; j ++){
int x; scanf("%d", &x);
if(i == j && stu[i] && !home[i]) add(i, i);
else if(x == 1 && stu[j] && (stu[i] && !home[i] || !stu[i])) add(i, j);
}
}
int cnt = 0, res = 0;
for(int i = 1; i <= n; i ++) match[i] = -1;
for(int i = 1; i <= n; i ++){
if(stu[i] && !home[i] || !stu[i]){
cnt ++;
memset(vis, 0, sizeof vis);
if(find(i)) res ++;
}
}
if(res == cnt) puts("^_^");
else puts("T_T");
}
return 0;
}
1. 贴板子过去了，还不是很懂bfs版本的KM,
2. 求的最小，所以全部取负数，跑KM就可以了
1. 可以转换成行和列分别一个集合的最小点覆盖问题，最小点覆盖=最大匹配
2. 相同的行列编号是要有所区分的
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010, M = 20010;
int n, m;
int match[N], vis[N];
int h[N], e[M], ne[M], idx;
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u){
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(vis[j]) continue;
vis[j] = 1;
if(match[j] == -1 || find(match[j])){
match[j] = u;
return true;
}
}
return false;
}
int xiongyali(){
int cnt = 0;
for(int i = 1; i <= 2 * n; i ++) match[i] = -1;
for(int i = 1; i <= n; i ++){
memset(vis, 0, sizeof vis);
if(find(i)) cnt ++;
}
return cnt;
}
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= 2 * n; i ++) h[i] = -1;
for(int i = 1; i <= m; i ++){
int x, y; scanf("%d %d", &x, &y);
y += n;
add(x, y); add(y, x);
}
printf("%d\n", xiongyali());
return 0;
}
问题转换成:每行保留一个黑色的点，并且这写黑色的点所在的行列不相同
假设存在某一行或者某一列没有的话，我们不能够通过行列变换使得这行或者这列
存在黑色点，而且其他行列不丢失黑色的点
1. 网格是一种天然的二分图
2. 一个骨牌恰好就是在二分图之间链接
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 210, M = N * N * 2;
int g[N][N];
int n, m;
int match[M], vis[M];
int h[M], e[M], ne[M], idx;
int dx[] = {0, 1, -1, 0};
int dy[] = {1, 0, 0, -1};
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int u){
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(vis[j]) continue;
vis[j] = 1;
if(match[j] == -1 || find(match[j])){
match[j] = u;
return true;
}
}
return false;
}
int xiongyali(){
int cnt = 0;
for(int i = 1; i <= n * n; i ++) match[i] = -1;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if( (i + j) % 2 && !g[i][j] ){
memset(vis, 0, sizeof vis);
if(find((i - 1) * n + j)) cnt ++;
}
}
}
return cnt;
}
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= m; i ++){
int x, y; scanf("%d %d", &x, &y);
g[x][y] = 1;
}
for(int i = 1; i <= n * n; i ++) h[i] = -1; idx = 0;
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= n; j ++){
if((i + j) % 2 && !g[i][j]){
for(int k = 0; k < 4; k ++){
int x = i + dx[k], y = j + dy[k];
if(x < 1 || x > n || y < 1 || y > n) continue;
if(g[x][y]) continue;
add((i - 1) * n + j, (x - 1) * n + y);
add((x - 1) * n + y, (i - 1) * n + j);
}
}
}
}
printf("%d\n", xiongyali());
return 0;
}
