dls的数论-初级课习题

小凯的疑惑

两个互质的数a,b,z=ax+by，求不能使用非负数x,y,表示的最大的z是多少
由扩展欧几里得知道ax+by=1都是有解的，但是解的x,y不一定都是非负的
另外通过通项公式我们知道x=x0+kb,y=y0-ka;
他其实就是一条直线，经过数形结合发现，

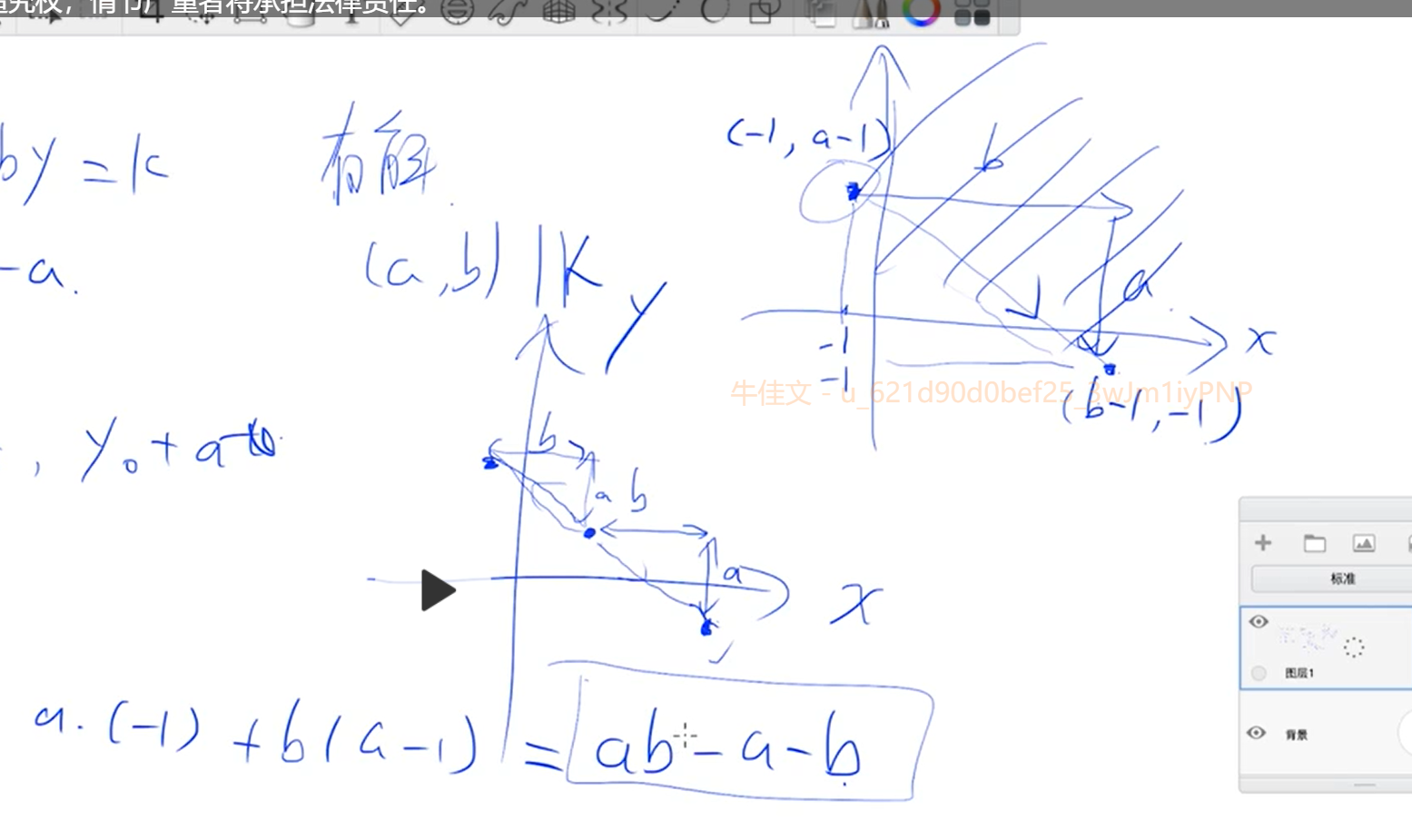
扩展欧几里得3

    1. 要变成最小的解x，这样后面不容易越界
    2. 学下正负数的向上向下取整

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;

LL floordiv(LL a, LL b){
    if(a % b == 0) return a / b;
    else if(a > 0) return a / b;
    else return a / b - 1; 
}

LL ceildiv(LL a, LL b){
    if(a % b == 0) return a / b;
    else if(a > 0) return a / b + 1;
    else return a / b;
}

LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}


int main(){
    int T; scanf("%d", &T);
    while(T--){
        LL a, b, d, l1, r1, l2, r2; scanf("%lld%lld%lld%lld%lld%lld%lld", &a, &b, &d, &l1, &r1, &l2, &r2);
        LL x, y;
        LL t = exgcd(a, b, x, y);
        if(d % t != 0){puts("0"); continue;}
        a /= t, b /= t, d /= t;
        x = x * (d % b) % b;
        y = (d - a * x) / b;
        // x = x * d, y = y * d;
        LL rk = min(floordiv(r1 - x, b), floordiv(y - l2, a));
        LL lk = max(ceildiv(l1 - x, b), ceildiv(y - r2, a));
        // cout << lk << ' ' << rk << endl;
        printf("%lld\n", max(0ll, rk - lk + 1));
    }
    return 0;
}

预处理求组合数

n,m的范围是1-1e7,O(n)预处理出来阶乘和阶乘的逆元，然后O(1)求组合数，逆元的处理也是O(n)的

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e7+10, mod = 1e9+7;
int fac[N], inv[N];

LL qmi(LL a, LL b, LL mod){
    LL res = 1 % mod;
    while(b){
        if(b&1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

void init(){
    fac[0] = 1;
    for(int i = 1; i <= 1e7; i ++) fac[i] = (LL)fac[i - 1] * i % mod;
    inv[10000000] = qmi(fac[10000000], mod-2, mod);
    for(int i = 9999999; i >= 0; i --) inv[i] = (LL)inv[i + 1] * (i + 1) % mod;

}

int C(int a, int b){
    if(b < 0 || b > a) return 0;
    else return (LL)fac[a] * inv[b] % mod * inv[a-b] % mod;
}

int main(){
    init();    
    int T; scanf("%d", &T);
    while(T--){
        int a, b; scanf("%d %d", &a, &b);
        printf("%d\n", C(a, b));
    }
    return 0;
}

分段打表处理组合数

    1. 每隔1e6处理出来一个答案，然后当计算某个阶乘的时候，直接从某个数值开始，往后计算1e6次就可以了
    2. 素数好像也可以这么处理,区间晒+分段打表

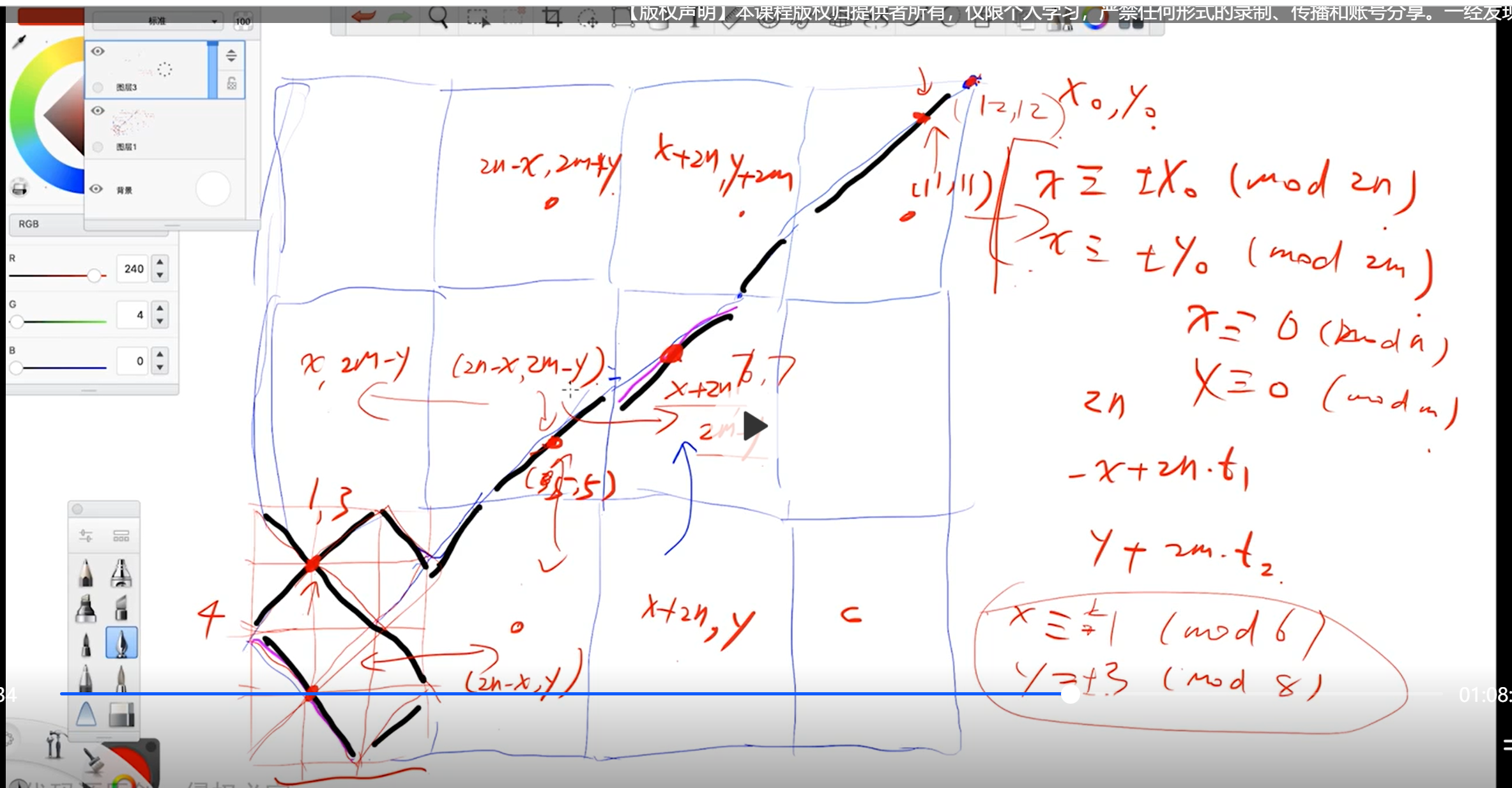
反射问题

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const LL inf = 1ll << 60;
int n, m, k;
int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }

LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}

LL merge(LL a, LL b, LL c, LL d){
    LL x, y;
    LL g = exgcd(b, d, x, y);

    if((c - a) % g) return inf;
    d /= g;
    LL t0 = ((c - a) / g) % d * x % d;
    if(t0 < 0) t0 += d;
    return b * t0 + a;
}

LL solve(int x, int y){
    // exgcd之前处理成最小非负整数比较好
    x = (x + 2 * n) % (2 * n);
    y = (y + 2 * m) % (2 * m);
    return merge(x, 2*n, y, 2*m);
}

int main(){
    scanf("%d %d %d", &n, &m, &k);
    LL T = (LL)n / gcd(n, m) * m;
    for(int i = 1; i <= k; i++){
        int x, y; scanf("%d %d", &x, &y);
        LL res = min({solve(x, y), solve(x, -y), solve(-x, y), solve(-x, -y)});
        if(res > T) printf("-1\n");
        else printf("%lld\n", res);
    }    
    return 0;
}

区间筛

1. 类似埃氏筛的方法，把质数的所有倍数全给删掉，复杂度和埃氏筛的复杂度差不多都是O(nloglogn)

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 1e7 + 10; 
int st[N];
int pr[N/5], pj[N], tot; 
void get_prime(int n){
    pj[1] = 1;
    for(int i = 2; i <= n; i++){
        if(!pj[i]) pj[i] = i, pr[++tot] = i;
        for(int j = 1; j <= tot && pr[j] <= n / i; j ++){
            pj[pr[j] * i] = pr[j];
            if(pr[j] == pj[i]) break;
        }
    }      
}

int main(){
    LL l, r, a, b; scanf("%lld %lld %lld %lld", &l, &r, &a, &b);
    get_prime(10000000);
    for(int i = 1; i <= tot; i ++){
        int p = pr[i];
        // 这里可以倒着进行，中止条件是j>=l 并且j>=p,如果j<=p,的话是不需要筛掉的
        // 如果是正着进行的话，需要保证是2*p开始，并且是大于等于l的一个p的倍数
        for(LL j = r / p * p; j >= l && j > p; j -= p) st[j - l] = 1;
    }
    unsigned int res = 0;
    for(LL i = max(2ll, l); i <= r; i ++) if(!st[i - l]) res = (res ^ (a * i + b));
    printf("%u\n", res);
    return 0;
}