dls的数论-中国剩余定理

简介

求解线性同余方程组：x=ai(mod mi)
mi之间两两互质，并不是所有的gcd=1，比如6，10，5就不是
则在模mi乘积的范围内的有唯一解
要求两两互质是由于求解的让Mi和mi是互质的
基本上useless,条件比较苛刻

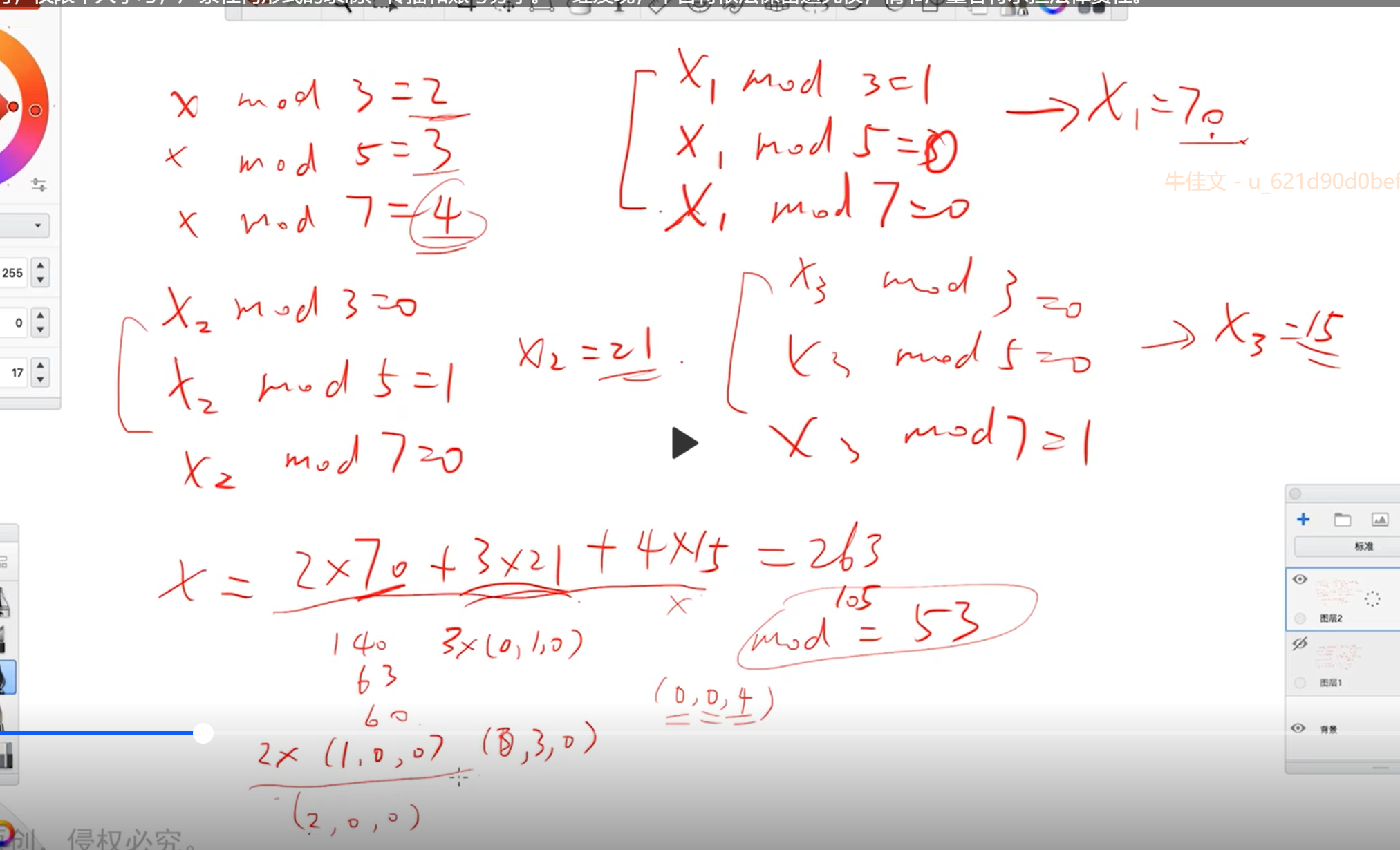
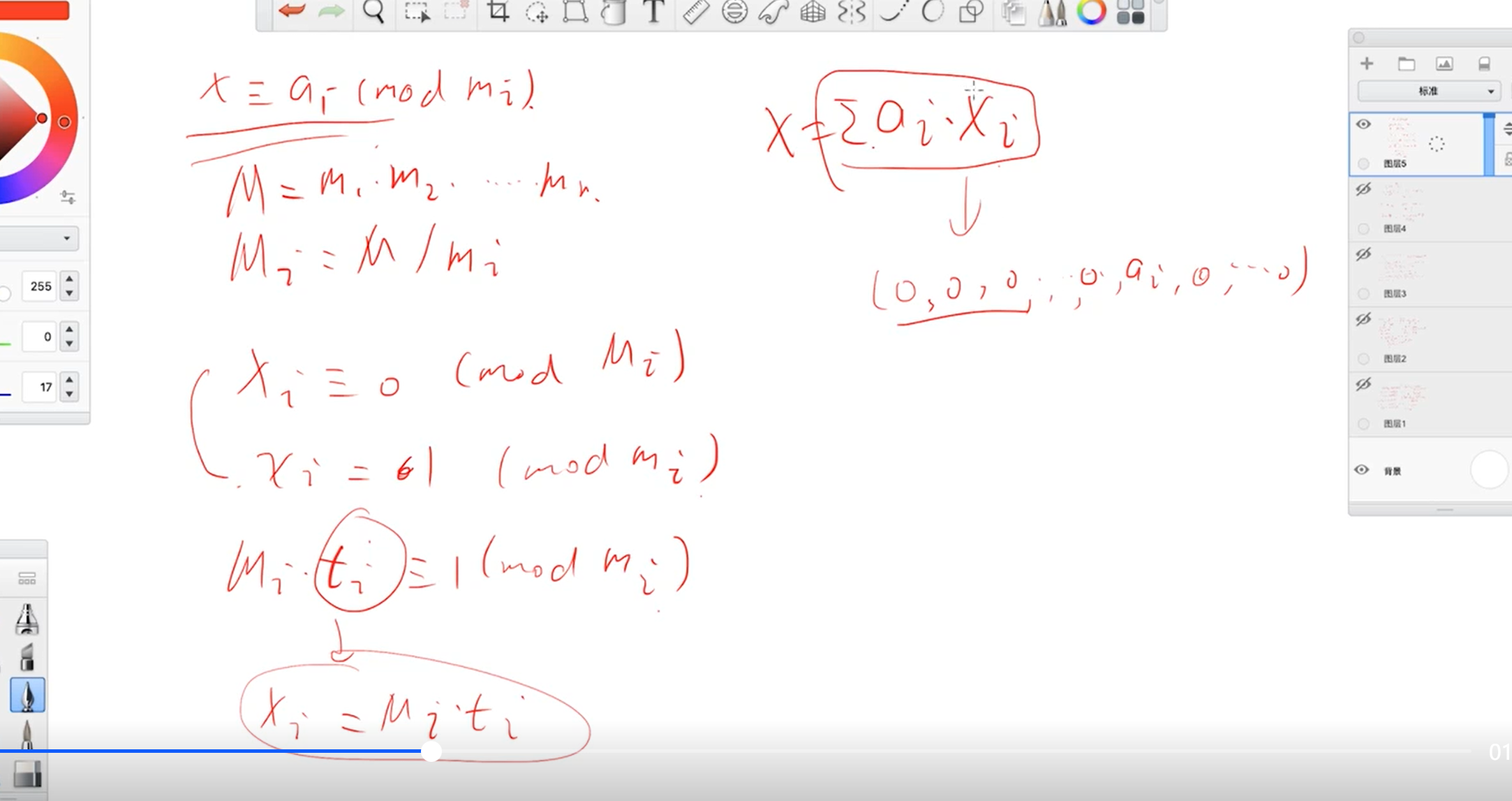
不互质增量法：不断地合并两个方程，最后只剩一个
两个模数不互质，要么在mod的地方有唯一解，要么无解

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;

LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}


void merge(LL &a, LL &b, LL c, LL d){
	if(a == -1 && b == -1) return ;
	LL x, y;
	LL g = exgcd(b, d, x, y);

	if((c - a) % g){
		a = - 1, b = -1;
		return ;
	}
	d /= g;
	LL t0 = ((c - a) / g) % d * x % d;
	if(t0 < 0) t0 += d;
	a = b * t0 + a;
	b = b * d;


}

void solve(){
	int n; scanf("%d", &n);
	LL a = 0, b = 1;
	for(int i = 0; i < n; i ++){
		LL c, d; scanf("%lld %lld", &c, &d);
		merge(a, b, c, d);
	}
	printf("%lld\n", a);
}

int main(){
	int T; scanf("%d", &T);
	while(T--){
		solve();
	}
	return 0;
}

题目链接：
给定一个组线性方程判断是否有解
考虑模合数，等于模这个数的素数幂是等价的

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

bool solve(){
    map<int , vector<PII> > h; 
    int n; scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        int a, b; scanf("%d %d", &a, &b);
        for(int p = 2; p <= b / p; p ++){
            if(b % p == 0){
                int psum = 1;
                while(b % p == 0) b /= p, psum *= p;
                h[p].push_back({psum, a % psum}); 
            }
        }
        if(b > 1) h[b].push_back({b, a % b});
    }
    for(auto P : h){
        int maxp = 0, num = 0;
        for(auto item : P.second){
            if(maxp < item.first) maxp = item.first, num = item.second;
        }
        for(auto item : P.second){
            if(num % item.first != item.second) return false;
        }
    }
    return true;
}

int main(){
    int T; scanf("%d", &T);
    while(T--){
        if(solve()) puts("Yes");
        else puts("No");
    }    
    return 0;
}