牛客数学-容斥
牛客容斥
两个子集的情况
设s是一个有限集,A和B是S的两个子集,求|S - A∪B| = |S| - |A| - |B| + |A∩B|
例:求1-n中,既不是2的倍数也不是3的倍数的数量
S = {1,....n}, A = {x∈S| 2|x}, B = {x∈S| 3|x}
|S - A∪B| = |S| - |A| - |B| + |A∩B| = n - n/2 - n/3 + n/6
求1-n的全排列,满足1,2不相邻,3,4不相邻的方案数
S = {所有的全排列}, A = {1,2相邻的全排列}, B = {3,4相邻的全排列}
|S - A∪B| = |S| - |A| - |B| + |A∩B| = n! - (n-1)! - 2*(n-1)! - 2*(n-1)! + 4*(n-2)!
三个子集的情况
|S-A∪B∪C| = |S| - |A| - |B| - |C| + |A∩B| + |A∩C| + |B∩C| - |A∩B∩C|
把n个物品放到三个盒子里面,满足每个物品至少有一个物品的方案数
S = {n个物品放到三个盒子的方案}
A ={第一个盒子没有物品的方案} B ={第二个盒子没有物品的方案} C ={第三个盒子没有物品的方案}
|S - A∪B∪C| = 3^n - 3*2^n + 3 - 0




方便求解某些性质有某些性质没有的题目


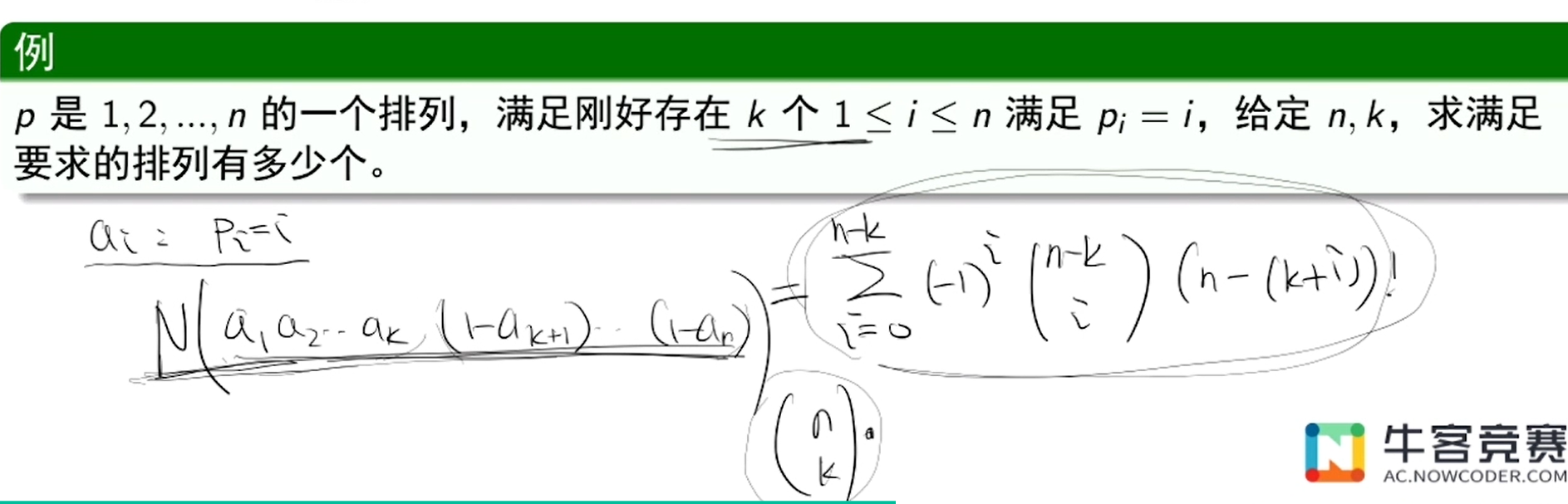


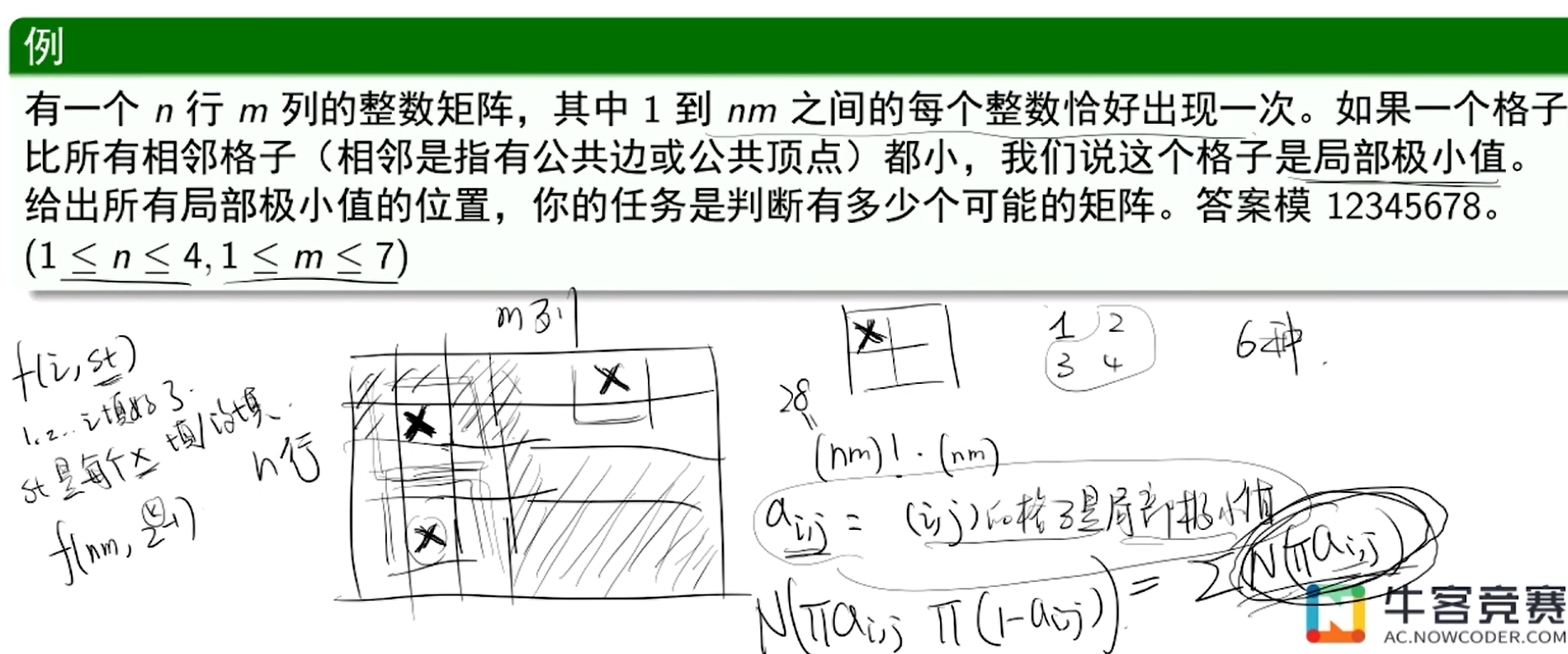
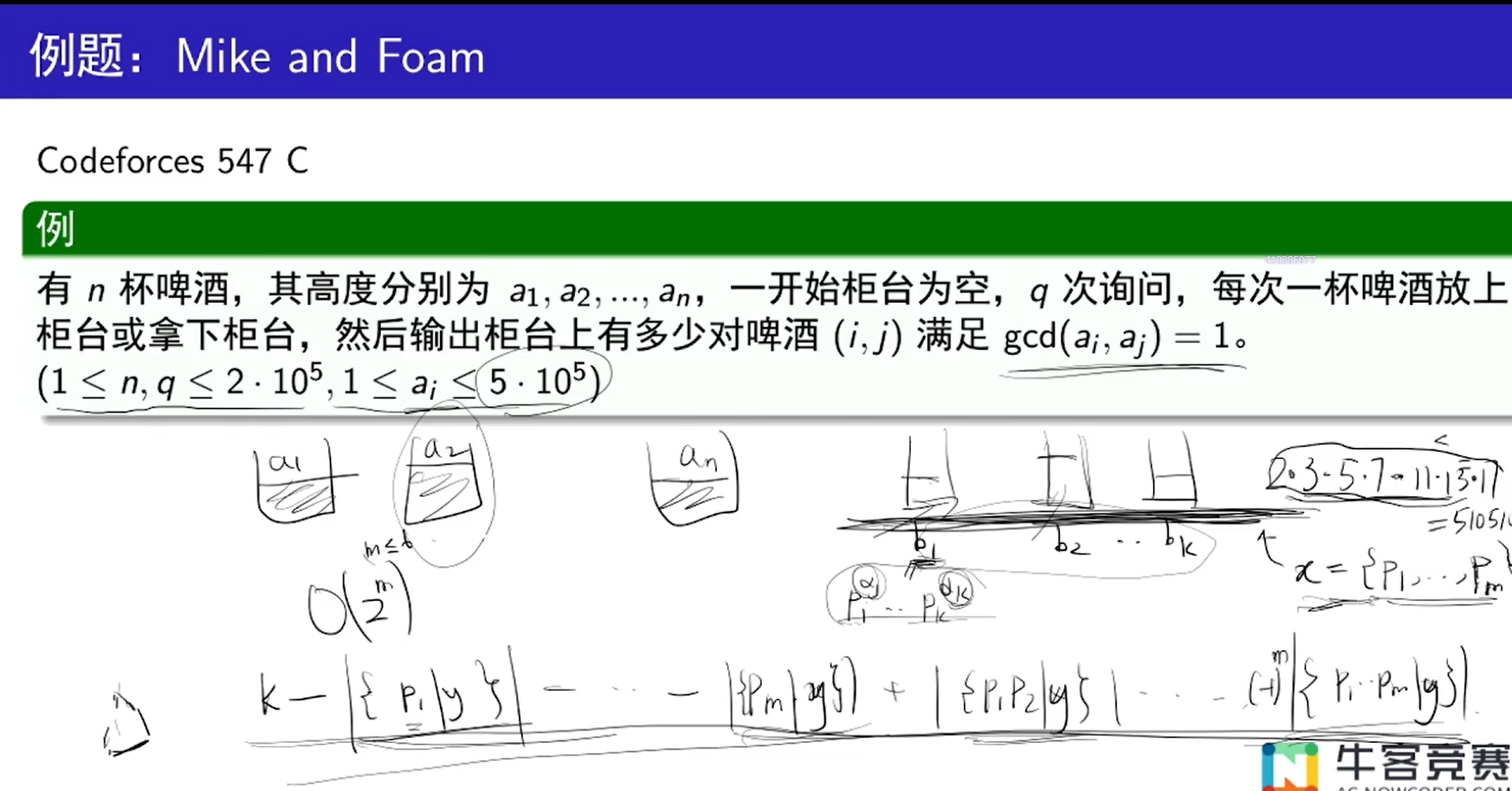


 浙公网安备 33010602011771号
浙公网安备 33010602011771号