Java数据结构与算法之链表
二、链表
1、介绍
链表是一个有序的列表，上一个数据连接下一个数据，通过链表指针连接，顺序不可改变。
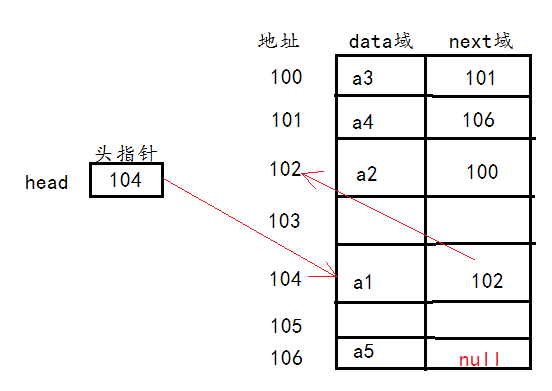
看一下链表在内存中的存储结构：
1. 链表是以节点的形式存储在内存空间中，是链式存储；
2. 每个节点包括data域（存储数据）和next域（存储指向下一节点的地址值）；
3. 虽然节点是有顺序的，但是在内存中去不是连续的，通过各个节点的连接实现有序存储；
4. 链表分为有头节点和无头节点，头节点内只存储next域，指向链表的第一个节点。
1.1 链表的初始化
// 定义节点，每个LinkedNode对象就是一个节点
class LinkedNode {
int val;
String name;
LinkedNode next; // 指向下一个节点
// 构造器
public LinkedNode(int val, String name) {
this.val = val;
this.name = name;
}
// 重写toString
@Override
public String toString() {
return "LinkedNode{" +
"val=" + val +
", name=" + name +
'}';
}
}
1.2 链表的添加
class SingleLinkedList {
// 定义一个头节点
LinkedNode headNode = new LinkedNode(0,"");
public LinkedNode getHead() {
return head;
}
// 添加节点到单向链表
// 1.找到当前列表的最后节点
// 2.将这个节点的next域指向要添加的节点
public void add(LinkedNode linkedNode) {
// 因为head节点永远指向第一个节点处，一旦移动的话就会找不到第一个节点
// 因此我们需要一个辅助节点
// 添加链表所以存在链表为空的情况，所以将temp设为头节点
LinkedNode temp = headNode;
while (true) {
// 因为temp此时是头节点，所以要判断.next是否为空
if (temp.next == null) {
break;
}
temp = temp.next;
}
temp.next = linkedNode;
}
// 遍历链表
public void showList() {
if (headNode.next == null) {
System.out.println("链表为空");
return;
}
// 同样的原因
// 因为上面已经判断了链表为空，所以这里可以直接将temp设置为第一个节点
LinkedNode temp = headNode.next;
while (true) {
// 这里的边界条件就可以直接判断temp是否为空了
if (temp == null) {
break;
}
System.out.println(temp.toString());
temp = temp.next;
}
}
}
这里我想谈一下本人之前对于辅助节点temp的一个错误认识：我之前的理解在于既然新建了一个辅助节点temp，那么之后的每一个temp = temp.next就是在重构了一个链表。
但现在有了新的理解，原先链表保持不变，改变的仅仅是temp，仅仅从temp的next域获得下一节点的地址，每一次temp = temp.next，就是把temp节点移动到正确的位置上，temp仅仅是原链表内部节点的映射。temp内部包含所映射节点的所有信息，包括data域和next域。
1.3链表的有序添加
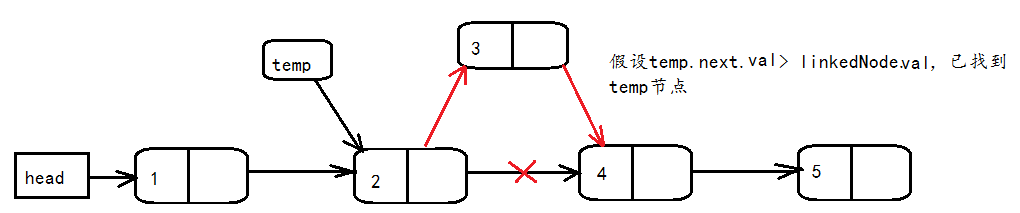
首先我们需要遍历链表，找到待添加节点linkedNode的正确添加位置。存在三种情况：位置在链表末尾；在链表中间；链表中已存在待添加节点。在末尾和已存在的情况较为好处理，我们来看下在链表中间情况。
假设我们已遍历找到节点temp的next节点比待添加节点linkedNode大，那么意味着待添加节点linkedNode应该位于temp和temp.next之间。所以我们让linkedNode指向temp.next，temp指向linkedNode即可。
public void addOrder(LinkedNode linkedNode) {
// 因为head节点永远指向第一个节点处，一旦移动的话就会找不到第一个节点
// 因此我们需要一个辅助节点
// 添加链表所以存在链表为空的情况，所以将temp设为头节点
LinkedNode temp = headNode;
boolean flag = false; // flag定义为链表内是否存在即将添加的节点
while (true) {
if(temp.next == null) { // 表示遍历结束，节点可直接添加在链表尾部
break;
}
if(temp.next.val == linkedNode.val) { // 表示已存在待添加节点
flag = true;
break;
}else if(temp.next.val > linkedNode.val) { // 表示已经找到位置，具体分析看图示
break;
}
temp = temp.next;
}
if(flag) {
System.out.println("要添加的节点已经存在了");
}else {
linkedNode.next = temp.next;
temp.next = linkedNode;
}
}
1.4 单链表节点的修改
思路就是遍历链表，找到对应节点，然后将新节点的内容重新赋值给旧的节点。
public void update(LinkedNode linkedNode) {
// 先判断链表是否为空
if (headNode.next == null) {
System.out.println("链表为空");
return;
}
LinkedNode temp = headNode.next;
boolean flag = false;
while (true) {
if(temp == null) {
break;
}
if(temp.val == linkedNode.val) {
flag =true;
break;
}
temp = temp.next;
}
if(flag) {
temp.name = linkedNode.name;
}esle {
System.out.println("未找到对应节点");
}
}
1.5 单链表节点的删除
思路依旧是遍历链表，找到待删除的节点temp.next。既然要删除temp.next，意思就是temp指向的是temp.next.next。
public void deletData(LinkedNode linkedNode) {
// 先判断链表是否为空
if (headNode.next == null) {
System.out.println("链表为空");
return;
}
LinkedNode temp = headNode;
boolean flag = false;
while (true) {
if(temp.next == null) {
break;
}
if(temp.next.val == linkedNode.val) {
flag =true;
break;
}
temp = temp.next;
}
if(flag) {
temp.next = temp.next.next;
}esle {
System.out.println("未找到对应节点");
}
}
2、双向链表的简单叙述
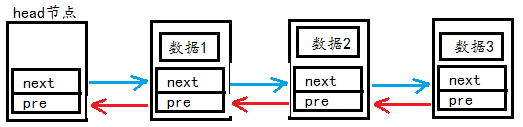
2.1 双向链表的初始化
// 定义节点，每个LinkedNode对象就是一个节点
class LinkedNode2 {
int val;
String name;
LinkedNode2 next; // 指向下一个节点
LinkedNode2 pre; // 指向前一个节点
// 构造器
public LinkedNode2(int val, String name) {
this.val = val;
this.name = name;
}
// 重写toString
@Override
public String toString() {
return "LinkedNode2{" +
"val=" + val +
", name=" + name +
'}';
}
}
2.2 双向链表的添加
class DoubleLinkedList {
// 定义一个头节点
LinkedNode2 headNode = new LinkedNode2(0,"");
// 添加节点到单向链表
// 1.找到当前列表的最后节点
// 2.将这个节点的next域指向要添加的节点
public void add(LinkedNode2 linkedNode) {
// 因为head节点永远指向第一个节点处，一旦移动的话就会找不到第一个节点
// 因此我们需要一个辅助节点
// 添加链表所以存在链表为空的情况，所以将temp设为头节点
LinkedNode2 temp = headNode;
while (true) {
// 因为temp此时是头节点，所以要判断.next是否为空
if (temp.next == null) {
break;
}
temp = temp.next;
}
temp.next = linkedNode;
linkedNode.pre = temp;
}
// 遍历链表
public void showList() {
if (headNode.next == null) {
System.out.println("链表为空");
return;
}
// 同样的原因
// 因为上面已经判断了链表为空，所以这里可以直接将temp设置为第一个节点
LinkedNode2 temp = headNode.next;
while (true) {
// 这里的边界条件就可以直接判断temp是否为空了
if (temp == null) {
break;
}
System.out.println(temp.toString());
temp = temp.next;
}
}
}
2.3 双向链表的修改
与单向链表的遍历一致
public void updata(LinkedNode2 linkedNode) {
if(headNode.next == null) {
System.out.println("链表为空");
return;
}
LinkedNode2 temp = headNode.next;
boolean flag = false;
while(true) {
if(temp == null) {
return;
}
if(temp.val == linkedNode.val) {
flag =true;
break;
}
temp = temp.next;
}
if(flag) {
temp.name = linkedNode.name;
}else {
System.out.println("为找到对应节点");
}
}
2.4 双向链表的删除
public void deletData(LinkedNode2 linkedNode) {
// 先判断链表是否为空
if (headNode.next == null) {
System.out.println("链表为空");
return;
}
LinkedNode2 temp = headNode.next;
boolean flag = false; // 标志是否找到待删除节点
while (true) {
if(temp == null) {
break;
}
if(temp.val == linkedNode.val) {
flag =true;
break;
}
temp = temp.next;
}
if(flag) { // 找到节点
// 将temp前一节点指向temp后一节点
temp.pre.next = temp.next;
// 如果是最后一个节点，则无法将后一个节点指向前一个节点，需要判断
if(temp.next != null) {
temp.next.pre = temp.pre;
}
}esle {
System.out.println("未找到对应节点");
}
}
3、Joseph问题
约瑟夫环问题（Joseph）又称丢手绢问题：已知 m 个人围坐成一圈，由某人起头，下一个人开始从 1 递增报数，报到数字 n 的那个人出列，他的下一个人又从 1 开始报数，数到 n 的那个人又出列；依此规律重复下去，直到 m 个人全部出列约瑟夫环结束。如果从 0 ~ (m-1) 给这 m 个人编号，请输出这 m 个人的出列顺序。
3.1 环形链表的初始化
class BoyLinkedNode {
int id;
BoyLinkedNode next;
public BoyLinkedNode(int id) {
this.id = id;
}
@Override
public String toString() {
return "BoyLinkedNode{" +
"id=" + id +
'}';
}
}
3.2 环形链表的添加
class BoyLinkedList {
private BoyLinkedNode first = null;
/**
* 创建约瑟夫环
* @param num 表示有num个人
*/
public void addNode(int num) {
// 判断输入是否合理
if (num < 1) {
System.out.println("人数太少");
return;
}
// 同样first节点不可移动，需要一个辅助节点
BoyLinkedNode curBoy = null;
// for循环往链表中增加节点
for (int i = 1; i <= num; i++) {
BoyLinkedNode boy = new BoyLinkedNode(i);
// 第一个节点需要单独添加
// 便于将头结点映射给first节点
if (i == 1) {
first = boy;
first.next = first; // 一个节点也需要成环形链表
curBoy = first; // 映射辅助节点
}
curBoy.next = boy;
boy.next = first;
curBoy = boy;
}
}
}
3.3 约瑟夫环的游戏部分
/**
*
* @param startId 表示从哪个节点开始数
* @param countNum 表示数几下
* @param num 表示一共有几个节点
*/
public void countBoy(int startId, int countNum, int num) {
// 先判断输入的合理性
if (startId < 1 || startId > num || num < 1) {
System.out.println("重新输入");
return;
}
// 需要一个辅助节点helperBoy与first配合，first寻找出局节点，helperBoy负责将出局节点的前后节点连接
// 不再需要原链表，所以first可以移动
BoyLinkedNode helperBoy = first;
// helperBoy节点到达指定节点
while (true) {
if (helperBoy.next == first) {
break;
}
helperBoy = helperBoy.next;
}
// first节点到达开始读数节点位置，helperBoy跟随
for (int i = 0; i < startId-1; i++) {
first = first.next;
helperBoy = helperBoy.next;
}
while (true) {
// 跳出循环条件，helperBoy==first
if (helperBoy == first) {
break;
}
// for循环寻找出局节点，
for (int i = 0; i < countNum-1; i++) {
first = first.next;
helperBoy = helperBoy.next;
}
System.out.printf("%d出队\n",first.id);
helperBoy.next = first.next; // 节点出局
first = first.next;
}
System.out.printf("%d出队\n",first.id);
}
