HashMap 源码分析

　　这次不以面试背题为目的，挑几个源码实现中值得玩味的点来分析一下。

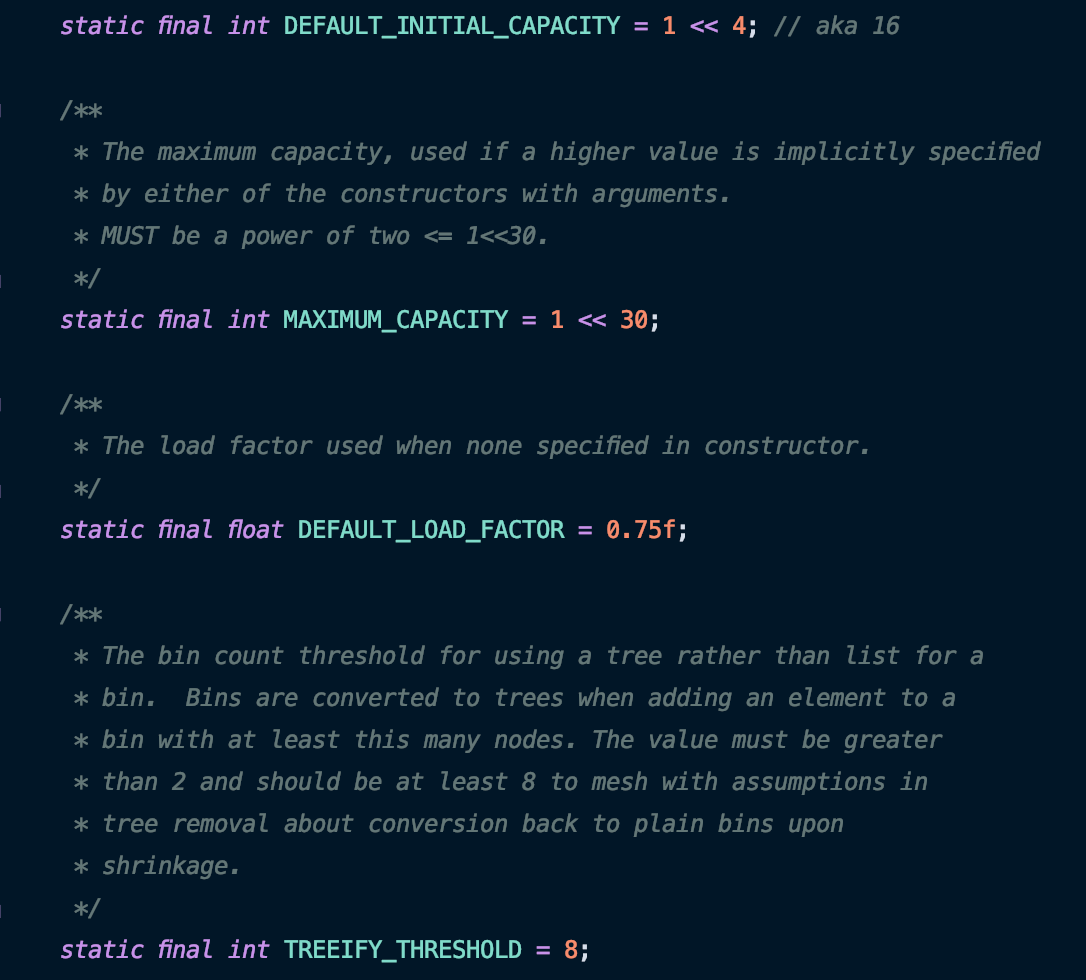
　　首先看几个初始化参数，在实现中 Lea 大爷大量的使用了二进制位移运算。比如 16 表示为 1<<4 ，1 073 741 824 表示为 1<<30 。由于计算机的物理特性，二进制运算的效率尤其是位移运算是高于直接使用十进制运算的。在非官方统计中，位运算比取余运算可以节约大约四十余个 CPU 晶振周期，按照Bruce Eckel给出的数据，性能大约可以提升5～8倍。在日常 CURD 的过程中，也可以在写好注释的前提下尽量的使用二进制位运算替代十进制运算。

负载因子（LOAD_FACTOR）

　　初始容量为 16，负载因子为 0.75。这是从 HashMap 诞生开始就没变过的定义，当元素数量达到当前容量的 75% 时，HashMap 会对数组进行扩容。该因子可在创建实例时指定。

　　由于哈希值在计算时需要映射到长度为 capacity 的数组下标上，因此哈希值的计算必然包含对数组长度的取模（取模的点后面说），在 put 方法中可以找到计算数组下标时需要对数组长度取模：

 

　　因此数组的剩余空间越小，数组下标冲突的几率越大，元素不得不存储在链表中，势必会降低插入、删除和查询效率。该值越高，数组的利用率也越高，但产生哈希冲突的概率也会随之变大。

　　在实际使用中，如果空间较紧张、且对时间要求不高时，可适当的调大该参数。

　　反之在空间较宽裕、且对时间要求较高时，可适当调小该参数。

取模运算

　　从上面的取模代码可以看出，HashMap 中 哈希值与容量的取模不是直接用的取模运算，而是用的与运算:（n-1）& hash 。

　　将取模运算转化为与运算是需要条件的，在 n 为 2 的整数幂时， hash%n = (n-1) & hash 的等式才成立。

哈希运算

　　哈希运算使用了对象本身的 hashcode 方法，用结果本身的高位与低位进行位运算。

　　在上一节的取模运算中，取模运算被降级为了与运算。这样在取模时，高位便不会参与运算。高位特征的丢失会增大取模时冲突的概率。

　　对此大爷采用了“防御性编程”策略，将哈希值的高位与低位进行异或来做二次哈希，这样，低位的值既包含低位的信息，也包含高位的信息，降低了下标冲突的概率。

素数在取模中的应用

　　在常识下，对一个数取模时，使用素数作为底数可以降低哈希冲突的概率。

　　证明取模时使用素数可以降低哈希冲突的概率，需要使用到数论中的“同余数”理论。

　　通过取余的方式，可以将一个大集合 A 映射到一个小集合 B 。

　　在 N 与 M 的最大公约数为 1 时，N%M 全体结果的集合为 R { 0,1,2,3...M-1 } 。R 中每一个元素 r 代表一个同余类 N 的集合。

　　比如对于 M = 3 ， r 为 0 代表着集合 N { 3,6,9,12 ... 3*n } 。

　　假设 N = kn , M = km 。N 与 M 的最大公约数为 k 。则：

　　N%M = r  >> N = Mq+r >> kn = kmq + r

　　其中 q 是商， r 是余数 。r 的取值范围为 { 0,1,2,3 ... M-1 }

　　但是因为 k 的存在： n = mq + r/k  >> r = k(n-mq)，也就是说，r 必为 k 的整数倍。

　　r 的取值范围缩减到了 { 0,1*k,2*k,3*k... } ，取值范围缩小了 k 倍。那么随着最大公因数的增大，冲突概率会成倍的增加。

　　所以在 N 与 M 最大公约数为 1 时，M 是素数还是合数压根不影响冲突的概率。

　　但在 N 与 M 最大公约数不是 1 时，会成倍的提高哈希冲突的概率。因此 M 选择素数，保证与 N 的最大公约数是 1 ，是可以降低哈希冲突的概率的。

　　HashTable 中以素数作为容量就是该原理的应用。

数组长度

　　之前介绍过，HashMap 的初始容量为 16。而在进行扩容时：

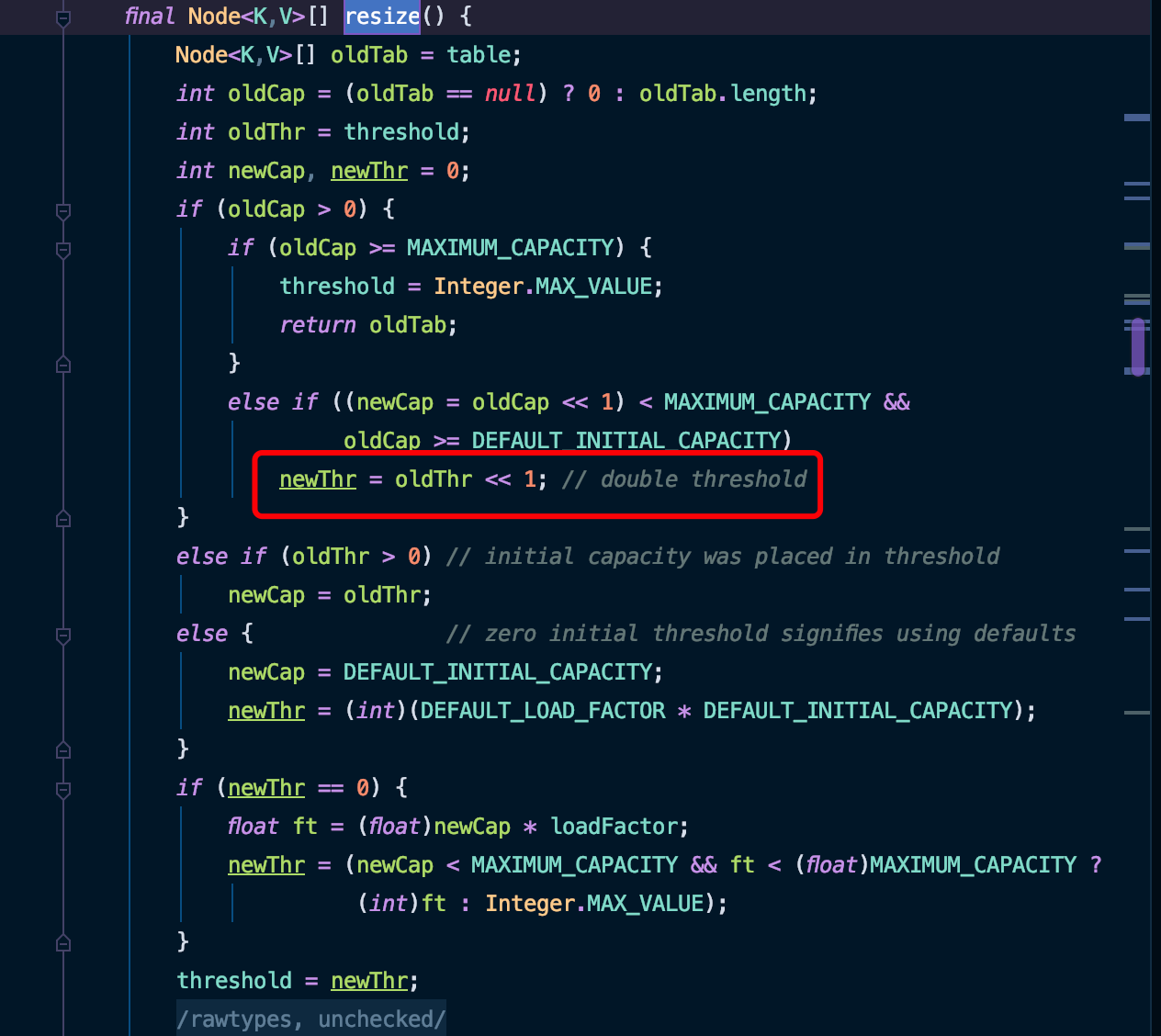
　　在 resize 方法中也可以看到，每次扩容后的容量为原容量的两倍。 16 是 2 的 4 次幂，在该策略下，数组的容量会一直是 2 的整数幂。

　　这与前面说的，尽量以素数为底数取模的原则相悖。

　　但是前面也提到过，哈希运算中的取模运算被降级为了与运算，提高了 5 ~ 8 倍的效率，而这种转化只有在底数为二的整数幂时才成立。

　　所以可以想到，容量取 2 的整数幂是出于提高取模效率的考量。

　　而对于哈希冲突，任何哈希算法都不可能完全的避免哈希冲突，因此在设计哈希表时必须设计冲突的处理方式。HashMap 中使用了拉链法来处理哈希冲突，同 hash 值的元素用链表连起来，在查找时一一比对。因此为了其它单元的效率，在一定程度上增加可控的冲突概率并不是不可行的。但是 Lea 大爷是如何得出该设计的综合效率会高于维护素数容量的综合效率，就不得而知了。

TREEIFY_THRESHOLD

　　jdk 1.7 及之前，处理哈希冲突的方式是拉链法。

　　但 1.8 中对拉链法中的链表做了进一步优化，默认的当链表长度大于 8 时，链表会转化为一颗红黑树，提高查询的效率。

　　可以想象在元素比较少时，构建红黑树的开销可能会大于红黑树带来的查询收益。

　　另外，红黑树不是完全平衡的，左右子树的高度差最大为两倍。因此在链表长度小于 8 时，树的高度小于 3 层，元素集中在一侧子树中的话在效率提升上并不明显。

　　因此在元素较少时采用链表存储，在元素较多时采用红黑树存储。至于长度的阈值为什么是 8 ，只能靠上面的猜测了。