Leetcode95 不同的二叉搜索树II 精致的分治

 

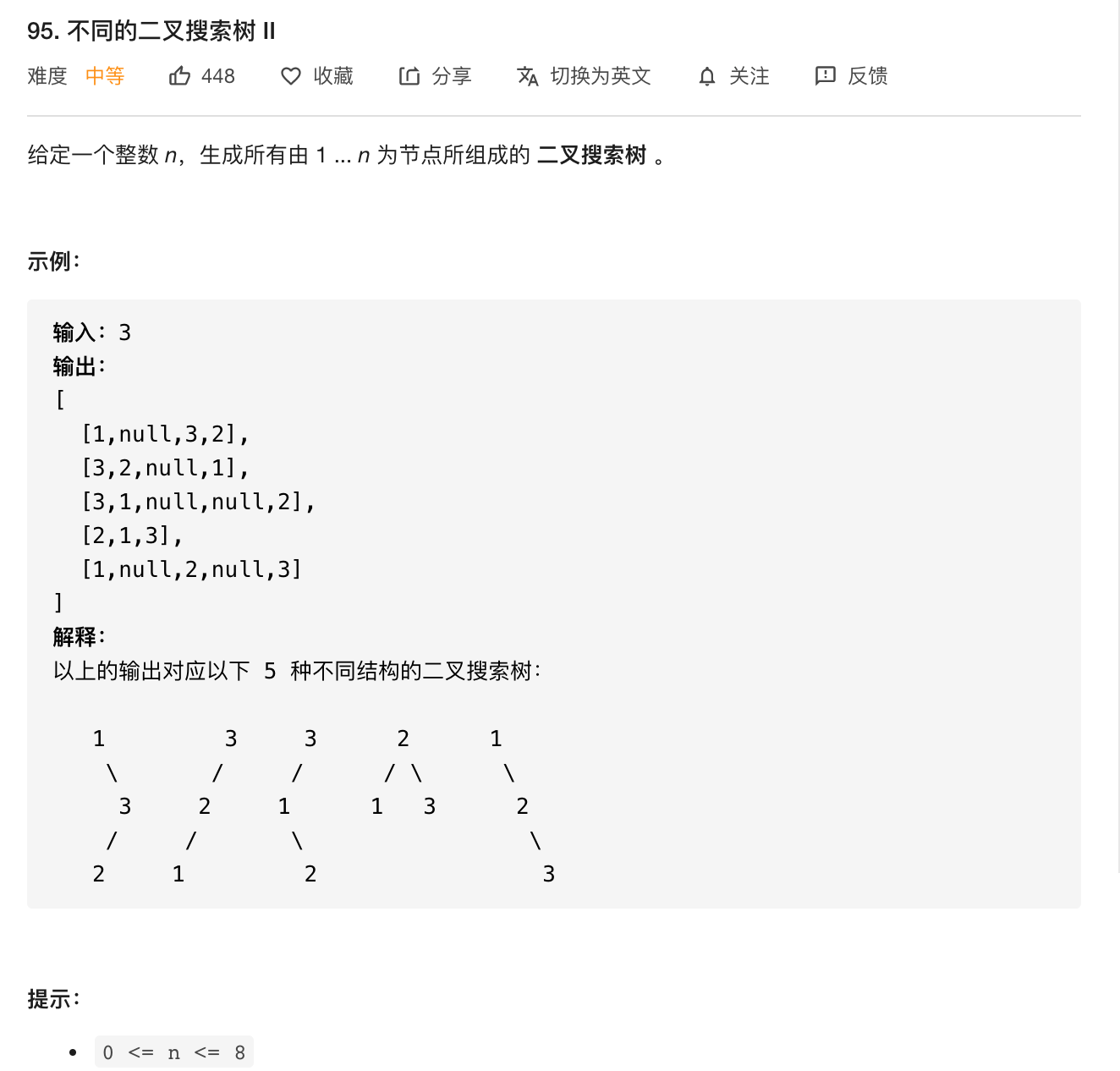
　　定义 G(b,e) 为 b 到 e 之间的元素可以组成的所有二叉搜索树。

　　在 b ，e 之间选出一个元素作为根节点， 则以该元素为根的所有可能的二叉搜索树为 G(b,i-1) ，G(i+1,e) 的笛卡尔积。

　　寻找顶层问题本身的递归结构，走的弯路最少。

public final List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new LinkedList<TreeNode>();
        }
        return generateTrees(1, n);
    }

    /**
     * @Author Niuxy
     * @Date 2020/7/6 10:48 下午
     * @Description 从问题本身找递归结构
     * 选取一个根节点分割数组，以该节点为根节点的所有可能的树为
     * 同类问题在两边子数组中解的笛卡尔积
     */
    public final List<TreeNode> generateTrees(int begin, int end) {
        List<TreeNode> anList = new LinkedList<TreeNode>();
        if (begin > end) {
            anList.add(null);
            return anList;
        }
        if (begin == end) {
            anList.add(new TreeNode(begin));
            return anList;
        }
        for (int i = begin; i <= end; i++) {
            List<TreeNode> left = generateTrees(begin, i - 1);
            List<TreeNode> right = generateTrees(i + 1, end);
            for (int j = 0; j < left.size(); j++) {
                for (int k = 0; k < right.size(); k++) {
                    TreeNode root = new TreeNode(i);
                    root.left = left.get(j);
                    root.right = right.get(k);
                    anList.add(root);
                }
            }
        }
        return anList;
    }