leetcode199 二叉树的右视图 DFS 与 BFS 解法
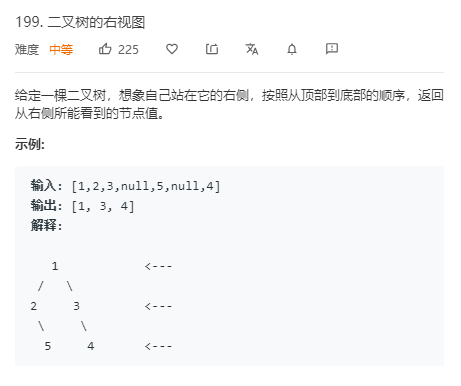
两种解法,DFS 与 BFS ,均已通过。对于 DFS 来说,我们需要从右到左遍历所有节点,并在每次遍历时记录当前深度。如果当前深度与结果数组长度相同,则为该层可以右视到的节点:
/** * @Author Nxy * @Date 2020/5/9 * @Description DFS 解法 */ List<Integer> reList = new LinkedList<Integer>(); public final List<Integer> rightSideView(TreeNode root) { if (root == null) { return reList; } rightSideViewDFS(root, 0); return reList; } public final void rightSideViewDFS(TreeNode node, int depth) { if (depth == reList.size()) { reList.add(node.val); } if (node.right != null) { rightSideViewDFS(node.right, depth + 1); } if (node.left != null) { rightSideViewDFS(node.left, depth + 1); } }
对于 BFS ,我们逐层遍历,并将每层最右侧节点记录下来。这就要求我们在遍历时可以对二叉树分层,这里我采用了两个队列,每层的元素放在不同的队列中。像两个桶,不断的倒过来倒过去的对二叉树进行分层:
/** * @Author Nxy * @Date 2020/5/9 * @Description BFS 解法 */ public final List<Integer> rightSideViewBFS(TreeNode root) { Queue<TreeNode> queue1 = new LinkedBlockingQueue<TreeNode>(); Queue<TreeNode> queue2 = new LinkedBlockingQueue<TreeNode>(); List<Integer> reList = new LinkedList<Integer>(); if(root==null){return reList;} queue1.add(root); while (queue1.size() != 0) { if (queue1.size() != 0) { TreeNode right = queue1.remove(); addChildNodes(queue2,right); reList.add(right.val); } while (queue1.size() != 0) { TreeNode right = queue1.remove(); addChildNodes(queue2,right); } if (queue2.size() != 0) { TreeNode right = queue2.remove(); addChildNodes(queue1,right); reList.add(right.val); } while (queue2.size() != 0) { TreeNode right = queue2.remove(); addChildNodes(queue1,right); } } return reList; } private void addChildNodes(Queue<TreeNode> queue,TreeNode node){ if(node.right!=null){queue.add(node.right);} if(node.left!=null){queue.add(node.left);} }
当你看清人们的真相,于是你知道了,你可以忍受孤独
分类:
数据结构与算法






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构