JAVA堆排序实现

堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

我们将给定的数组想象成一个完全二叉树，那么数组元素与二叉树节点的对应关系如下：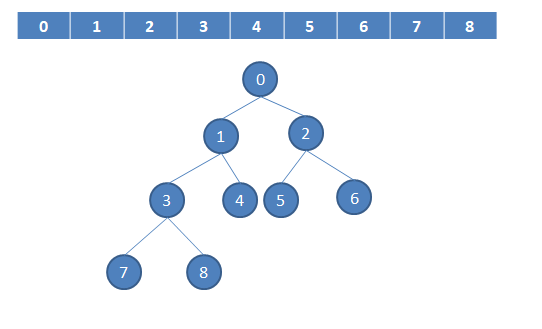

可以看到 0 的子元素为 1 、 2 ， 1 的子元素为 3 ， 4 、 3 的子元素为 7 、 8。

及对应关系为：下标为 n 的元素的左子元素下标为 2n+1 , 右子元素下标为 2n+2 。根据该对应关系，我们可以将数组看作一个满足堆积性质的完全二叉树，借助二叉树的性质来进行排序。

简单来说：堆排序是将数据看成是完全二叉树、根据完全二叉树的特性来进行排序的一种算法。

按堆积性质，堆可以分为 最大堆 和 最小堆：最大堆要求节点的元素都要不小于其孩子，最小堆要求节点元素都不大于其左右孩子。那么以最大堆为例，处于最大堆的根节点的元素一定是这个堆中的最大值。

下面仅讨论最大堆：

我们从最底层节点开始构建最大堆，依次向上。因为每个节点的两棵子树已经被我们构建为了最大堆，所以选择两个子树的根节点及当前节点中的最大值即为以当前节点为根的树中的最大值。

及自下向上构建最大堆时，我们在每一层只需比较根元素及其两个孩子节点即可正确的构建最大堆。我们对一个两层的完全二叉树的建堆代码如下：

/**
     * @Author Nxy
     * @Date 2019/12/5
     * @Param head:堆顶位置；end：序号为end及之前的元素可以用来构建堆
     * @Return
     * @Exception
     * @Description 将一个只有三个节点的堆变为最大堆
     */
    public static void sortNode(int[] nums, int head, int end) {
        if (head < 0) {
            throw new RuntimeException("堆顶超过左边界");
        }
        int length = nums.length;
        //左子节点坐标
        int left = head * 2 + 1;
        //右子节点坐标
        int right = left + 1;
        //判断左子节点是否存在
        if (left <= end) {
            //如果左子节点更大，交换
            if (nums[left] > nums[head]) {
                int temp = nums[head];
                nums[head] = nums[left];
                nums[left] = temp;
            }
        }
        //判断右子节点是否存在
        if (right <= end) {
            //如果右子节点更大，交换
            if (nums[right] > nums[head]) {
                int temp = nums[head];
                nums[head] = nums[right];
                nums[right] = temp;
            }
        }
    }

基于对两层完全二叉树的建堆，我们可以将整个数组构建为一个最大堆：

    /**
     * @Author Nxy
     * @Date 2019/12/5
     * @Param
     * @Return
     * @Exception
     * @Description 排序一个整堆, 最底层最右边的叶子节点序号为end。最小的非叶子节点序号为 (end - 1) / 2
     * 排序是从最小的非叶子节点构建堆，向上直到根节点
     */
    public static void sortHeap(int[] nums, int end) {
        int length = nums.length;
        for (int i = (end - 1) / 2; i >= 0; i--) {
            sortNode(nums, i, end);
        }

    }

但是需要注意的是，最大堆使得以二叉树的角度理解数组，数组是符合堆积性质的，但数组并不是有序的。

以下面的最大堆为例：

可以看出，这是一个符合堆积性质的最大堆，但它并不是一个有序的数组，我们将其还原成数组：

这是因为，堆积性质只规定了根元素与孩子节点之间的大小关系，至于左孩子与右孩子之间的大小关系是没有限制的。也就是说，根节点一定大于两个孩子节点，但两个孩子节点间是无序的。

所以构建最大堆对于排序来说，意义是为我们找到了序列中的最大值，而不是让整个数组变的有序。

我们可以通过不断的通过建堆找出剩余元素中的极值来完成排序。我们完整的排序操作如下：

1. 将整个数组构建为一个最大堆，此时 nums[0] 即是数组中的最大值。

2. 将 num[0] 与 nums[length-1] 互换。

3. 将 0到length-2 将的元素构建为最大堆，此时 nums[0] 即是数组中除第一步找出的最大值外的的最大值。

4. 将 num[0] 与 nums[length-2] 互换。

5. 重复上述操作，直到可以用来构建堆的元素仅剩 nums[0]， 整个数组排序完毕。

可以看到，我们对 n 个元素建堆一次，需要 log₂n 次计算，而整个过程需要建堆 n 次，所以时间复杂度为 O(nlog₂n ) 。而我们在排序过程中采用了互换位置的就地排序方式，没有使用额外的空间存储数组，空间复杂度为 O(1) 。因为我们进行了多次建堆，数值相同的元素被冒到堆顶的顺序是不确定的，因此堆排序是不稳定排序。

基于上面展示的两个方法，堆排序的实现为：

    /**
     * @Author Nxy
     * @Date 2019/12/6
     * @Param
     * @Return
     * @Exception
     * @Description 堆排序
     */
    public static void heapSort(int[] nums) {
        if (nums == null) {
            throw new RuntimeException("数组为空");
        }
        int length = nums.length;
        for (int i = length - 1; i >= 0; i--) {
            sortHeap(nums, i);
            int temp = nums[0];
            nums[0] = nums[i];
            nums[i] = temp;
        }
    }