从三数之和看如何优化算法,递推-->递推加二分查找-->递推加滑尺

人类发明了轮子,提高了力的使用效率。
人类发明了自动化机械,将自己从重复的工作中解脱出来。
提高效率的方法好像总是离不开两点:拒绝无效劳动,拒绝重复劳动。人类如此,计算机亦如是。
前面我们说过了四数之和的递归和递推思路,递归和递推是一个比较通用的解题方法,我们可以以此为基础对解空间有一个整体的认识,优化出更加高效的算法。下面我们以三数之和为例来看一下,如何从最简单的递归一步一步得到更加高效的解法。题目很简单,主要说一下优化的思路:

由于之前说过递归的思路,那这次我们就先用递推来解题。
由于解空间的结构非常简单,nums.length棵3层的nums.length叉树的遍历。我们使用三重for循环来遍历这个解空间,每一层为从nums数组中取出一个数,最终便可以遍历完所有三个数的组合,伪代码:
int length=nums.length; for(int i=0;i<length;i++){ for(int j=0;j<length;j++){ for(int k=0;k<length;k++){ if(nums(i)+nums[j]+nums[k]==0){ 得到答案 } } } }
上述代码可以遍历出nums中元素所有的三个元素的组合,但需要注意的是其中包含了重复的元素。重复的原因是我们每层循环都是从头取到尾,而没有考虑上层循环已经做过的事。比如:

我们的i层for循环在遍历到num0时,其实应取到了包含num0的所有组合。而当i层for循环遍历的num1时,j层for循环还是遍历了num0,这就造成了结果的重复。0,1,2----1,0,2-----2,1,0其实是排序不同但实质相同的结果集。我们在j层循环不应该再去试探i层循环已经走过的元素,同理k层循环不应该去试探i,j两层循环已经走过的元素。从而避免遍历到排序不同但实质相同的结果。将上面的代码修改一下:
int length=nums.length; for(int i=0;i<length;i++){ for(int j=i+1;j<length;j++){ for(int k=j+1;k<length;k++){ if(nums(i)+nums[j]+nums[k]==0){ 得到答案 } } } }
经过这一步的去重,我们得到了最原始的解法(结果的排序去重就不说了,主要说计算过程的优化思路):
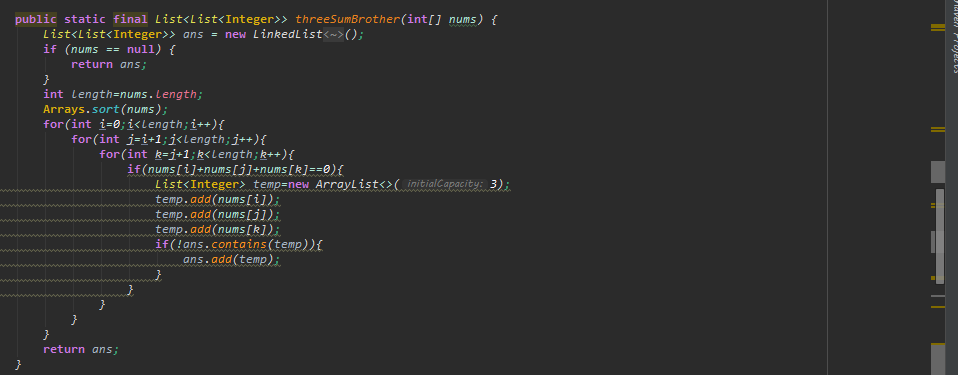
其实优化的第一步就是去除重复计算,但由于本题题目要求的特殊性(不允许有重复的结果),去除重复计算我们仅能得到最原始的解法。如果没有重复计算可以被优化掉,下一步我们应该考虑的是无效计算。
我们一步一步来看,我们最终要求的是和为0的三个数。在确定了第一个数和第二个数之后,我们便已经知道了我们需要的第三个数是什么。在这种情况下,第三层循环还在傻傻的遍历便显得有些多余,我们可以在k层遍历的区间内进行二分查找来找到我们要的第三个数,将k层循环的时间复杂度从O(N)降低到O(log2N)!
二分查找有问题的同学可以看我之前的随笔,传送门--->二分查找java实现:https://www.cnblogs.com/niuyourou/p/11885123.html
我们来看一下将第三层优化为二分查找后的代码:
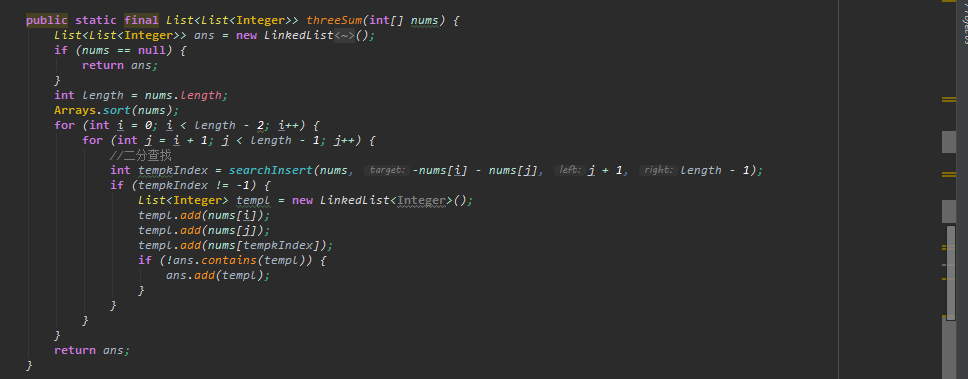
我用相同的数组比较了一下两种算法的效率:

可以看到速度的提升还是很明显的。但好像还是差那么一点,直觉告诉我即使第三层使用了二分查找我们的算法还是存在着无效计算。我们用优化第三层的思路来想一下,如果第一个数已经确定,那么我们的问题便是从剩下的元素中找出和为0-第一个数的组合。
我们想象一下,如果一个数组已经排序,那么对于一个确定的数A和target来说,在结果不重复的要求下,数组中只能唯一有一个数可以满足与A的和为target。我们可不可以从外侧(从数组中的两个极值开始)开始,一步一步将无解的元素排除来减少我们的无效计算呢?

如上图所示,对于一个已经排序的数组。我们可以维护两个指针来维护一个窗口。指针的移动原则是:当确定指针指向元素在数组中没有对应元素使它们的和为target时我们移动指针;每个指针只向一个方向移动,确定了无解的元素我们不再试探;移动过程如下:
此时两个指针在数组的两头,如果两个指针所指向的两个数的和大于target,说明左右的数均太大。需要有一个指针左移,因为左侧指针无法左移,所以左移右指针,同时我们确定,右指针走过的“7”元素在数组中是无解的。

两个数的和依然大于target,依然为了不越界,我们继续左移,一直移动到2。至此,右边指针走过的所有元素在数组中均没有一个匹配的值能使的两个元素的和为target。也就是说,4/5/6/7均无解,后面无论的所有计算我们均不需要再考虑这些元素。

此时两个数的和小于target,说明我们选中的两个数太小,需要有一个指针右移。因为对右侧指针来说,其右边的元素我们已经确定无解,不再考虑。所以我们将左指针右移。此时我们得到了-2,2这对组合。
可以看到,在我们的移动过程中,指针走过的元素或者无解,或者有解但已经被我们记录下,当两个指针相遇时我们便可以得到所有组合。
总结一下我们的移动过程如下:
第一次移动
此时指针在数组的两端。如果我们得到的和大于target,右指针左移;反之左指针右移,这样我们可以确保指针走过的元素在数组中是无解的。
后续移动
不管第一步移动的是哪个指针,我们都只能再进行两个动作:左指针右移或右指针左移。因为左指针左边或右指针右边要么是边界,要么是我们已经确定了的在数组中无解的元素。上述移动策略保证了两个指针走过的元素在数组中是无解的。
在移动的过程中我们遇到和为target的组合便记录下来,等两个指针相遇时我们便得到了该数组中所有和为target的组合。
这样内部两层for循环的计算次数被我们缩减为了N次,相当一一次遍历。相对于二分查找法的N*log2N次,性能又有了提升。
代码如下: 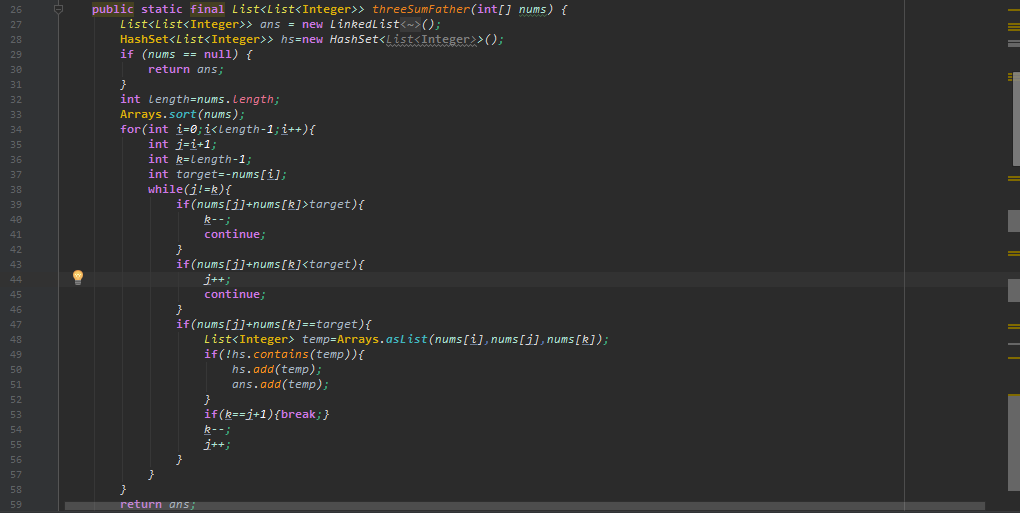
我们来看一下计算效率:

我们的优化过程如下:
1. 通过控制内外层循环的范围避免重复计算。
2. 通过二分查找优化最内部的循环,避免了一部分无效计算。
3. 而第三种方法(滑尺法)的思路是,如何更高效的判断一个元素有没有解,无解则略过来避免无效计算。
可以看出,避免重复计算是比较容易的。动态规划也是这种思路,只是使用的是DP表缓存。但在避免无效计算时,方法不固定,套路多。需要我们结合生活经验和想象,数学都是从猜想开始的,这点上算法也类似,所以还是要多刷题多看书,去积累经验和思路,不断的刷新我们的上限。与各位共勉!(有更好的方法欢迎指出呀!)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号