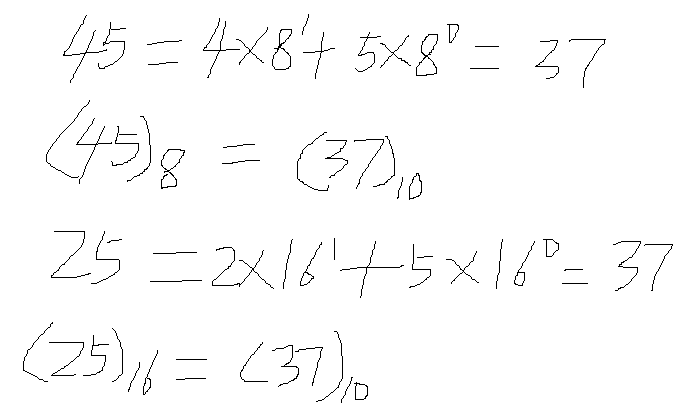计算机进制之间的转化

进制，也就是进制位。我们常用的进制包含：二进制、八进制、十进制，十六进制；

它们之间区别在于数运算时是逢几进一位，二进制是逢二进一位，十进制（0~9）是逢10进一位。

我们来看一幅图：

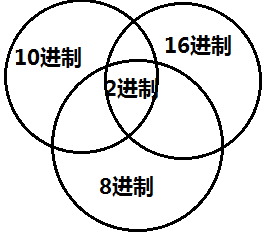
二进制：0-1，满2进1。

十进制：0-9，满10进1。

八进制：0-7，满8进1。

十六进制：0-9，A-F，满16进1，用0x开头表示。

1.1 如何将十进制转换成二进制数？

首先，我们需要先了解一下，什么是二进制数？二进制数是用0和1的数码来表示的数，它的基数是2，进位规则是“逢二进一”，借位规则是“借一当二”。

学习了理论以后，我们来看一个例子：

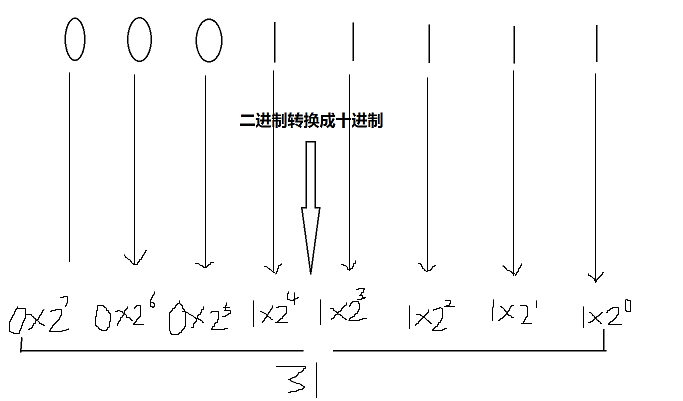
如何将十进制31转换成二进制数？下面是转换的方法。

 

以上，我们可以得出结果：（31）10 = （00011111）2；

方法：十进制转换成二进制，采用的是将被转化的十进制数连续除以2，取余数。能被2整除的余数标记为0，不能被2整除的余数标记为1。直到最后的商为0，取余数完毕（余数为权位上的数）。然后将得到的余数自下而上的排列开来。我们知道一个字节是8位，高位不足的，我们补0。

注意：1(被除数)÷2（除数） = 0（商）--- 1（余数），即0（商）×2（除数） + 1（余数）= 1（被除数）。

这里我们可以得到余数和除数的关系，余数一定要小于除数，余数 ＜ 除数。

1.2 如何将十进制转二进制数？

我们接着上面的例子，来讲讲如何将二进制数00011111转换成十进制？

方法：将二进制的数按权位展开，相加即得十进制数。

 

 

 

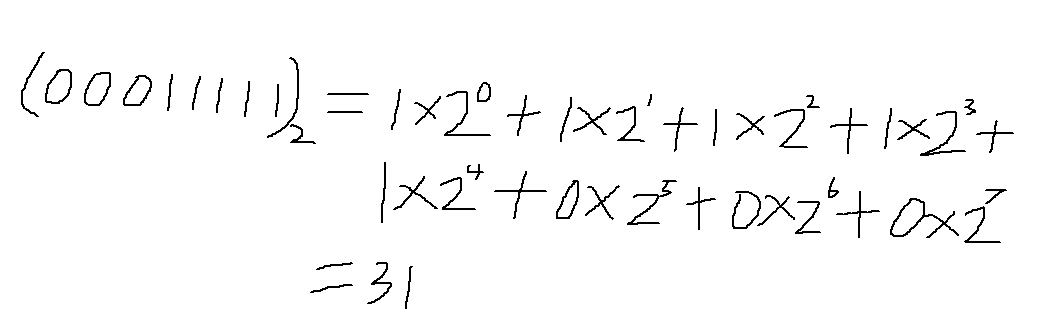
以上，我们可以得出结果：（00011111）2 = （31）10；

我们知道，十进制，是逢十进一，个位（1）、十位（10）、百位（100）等的确定，我们可以得出都是10的倍数。

同理，二进制的其实也是一样的，即为逢二进一，个位（1）、十位（2）、百位（4）等的来确定。

但是不同的是，一个二进制的数，有8个字节，通过0和1来来表示。如（31）10 = （00011111）2；

我们都知道，1个字节等于8个二进制位。

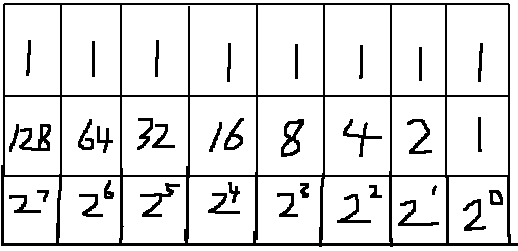
8个二进制位，分别代表了，1，2，4，8，16，32，64，128。字节是8位的数据单元，一个字节可以表示0－255的十进制数据（全部为0是0，全部为1是255）。

那下面，我们接着来思考，如何表示（37）10的二进制数呢？下面我们来动动手吧。

37 = 32 + 4 + 1 = 2^5 + 2^2 + 2^0 = （00100101）2。

由上可知，占了位有数字的，表示1，没有的都有0来填充。

当然，我们也可以参照上面的方法（竖式除以2取余倒取）来将一个十进制的数转换成二进制。

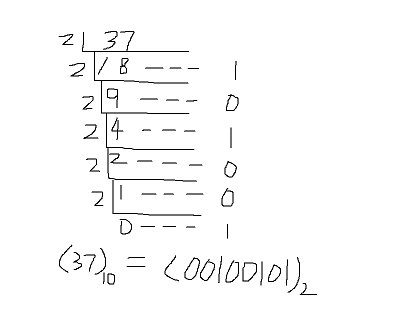
同样，我们可以求出结果为：（37）10 = （00100101）2

2.1 如何将二进制转换成八进制数？

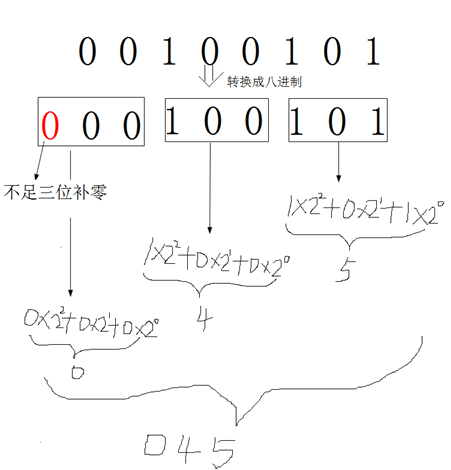
方法：3位二进制数按权展开相加得到1位八进制数。（注意：3位二进制数转成八进制数是从右到左开始转换，不足时补0）。

 第一步，将二进制取三合一；

 第二步，按权展开求合；

 第三步，得到八进制数。

2.2 如何将八进制转换成二进制数？

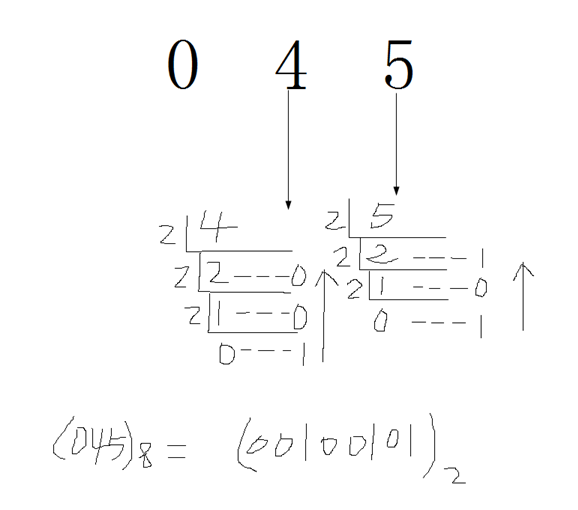
3.1 如何将二进制转换成十六进制数？

方法：4位二进制数按权展开相加得到1位十六进制数。（注意：4位二进制数转成十六进制数是从右到左开始转换，不足时补0）。

 第一步，将二进制取四合一；

 第二步，按权展开求合；

 第三步，得到十六进制数。

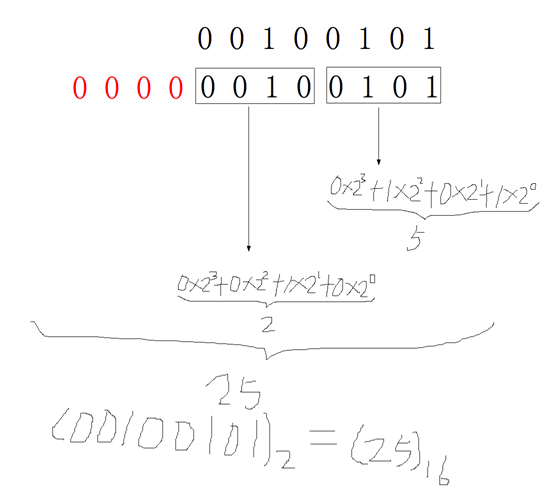
十进制和十六进制对应表：

3.2 如何将十六进制转换成二进制数？

方法：十六进制数通过除以2取余数，得到二进制数，每个十六进制数为四个二进制数位，不足的在最左边补0。

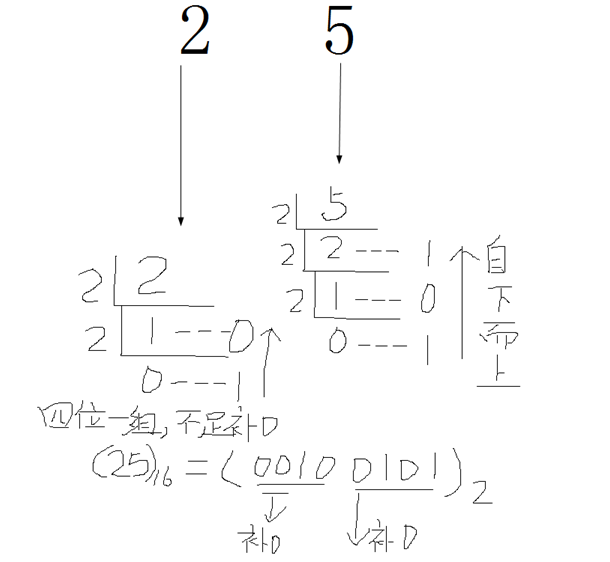
4.1 如何将十进制转换成八进制或是十六进制？

方法：直接把十进制转换成八进制或是十六进制，按照除以8或是16取余，直到商为0为止。

（37）10 = （45）8

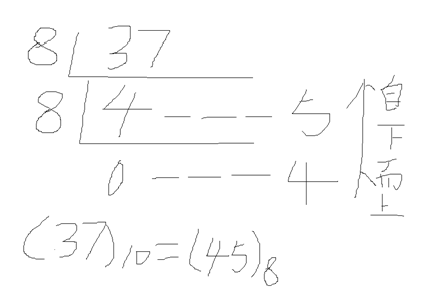
（37）10 = （25）16

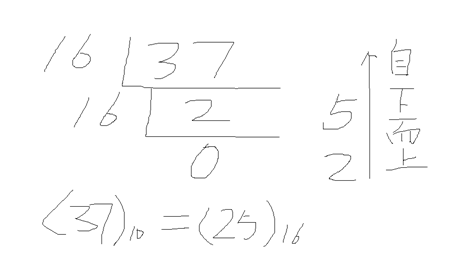
4.2 如何将八进制或是十六进制转换成十进制？

方法：把八进制或是十六进制按权展开，相加得到十进制数。