LQR算法如何跟随变化的期望状态
开门见山,通过LQR的能量函数可以看出,LQR算法是将状态量控制到零(关于能量函数请看我的随笔:LQR要点),但实际控制中我们希望状态量能够跟随期望值
下面将会解决如何用LQR算法跟随变化的期望值:
分为两个子问题:
1 如何稳定在期望值
设实际状态量x,期望状态x_ref,将实际状态量与期望状态作差,记为x_delta,x_delta作为我们要控制的状态量
x_delta = x - x_ref
完成迭代:x_delta(i+1) = A * x_delta(i) + B * u(i)
其中u(i) = -K * x_delta(i) K=dlqr(A,B,Q,R)
我们需要的是状态量x
x = x_delta + x_ref
输出x我们会发现状态量就可以稳定在期望值了(LQR控制需要一定时间,因此要适当取迭代次数,另外增大Q可以加速收敛)
2 跟随变化的期望值
通过调试LQR,我们会发现LQR需要一定时间才可以稳定在期望值,想要达到更好的观测效果我们需要把期望状态从连续信号转化为阶跃信号,实际控制中我们得到的信号或是期望的信号都是阶跃的离散的,因此阶跃信号的期望状态更贴近现实:
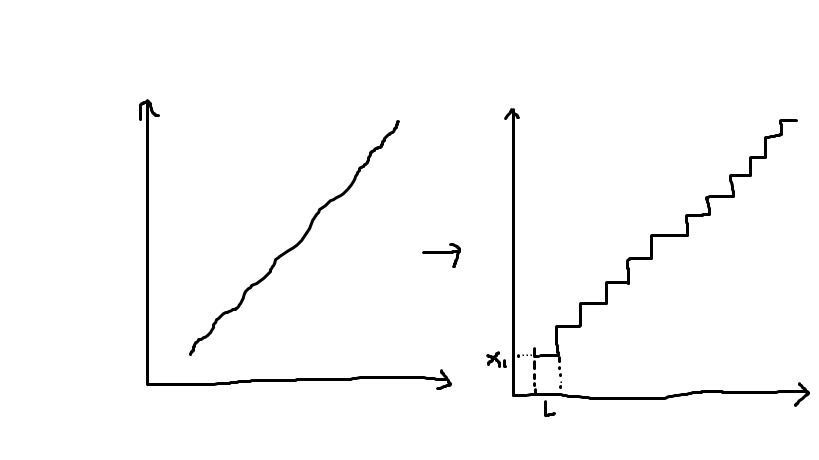
并且L要保证此LQR算法需要在L期间内能够稳定到X1
控制效果会变成: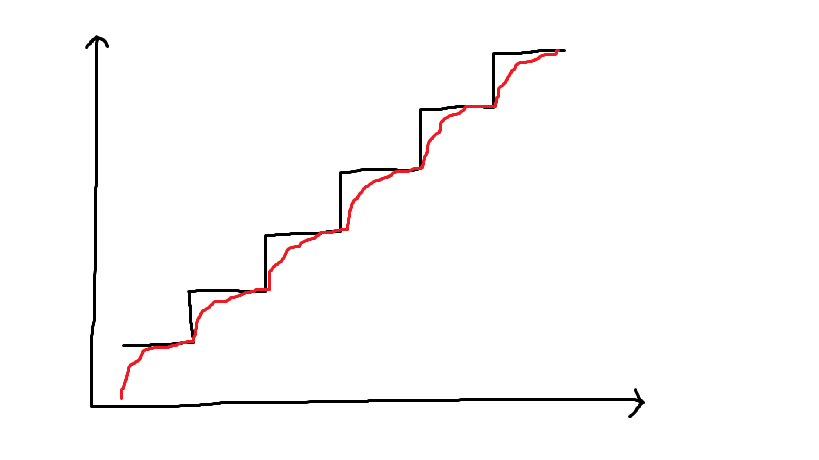 ,
,



