求解二次规划问题——外点罚函数法/内点罚函数法

外点罚函数法

做法就是在可行域之外设置障碍，可解决等式和不等式约束问题，但求出的最优解往往不在可行域内。

将约束条件转化成函数表达式的一部分，使新的函数式变为无约束的二次规划问题：

约束条件转换：

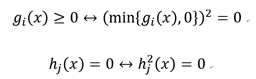
 将等式和不等式转换后的式子融合：

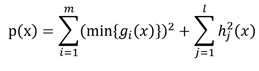
算法步骤：

1 确定初始点x0，初始罚银子Mk（可取M1=1），设置精确度

2 用解析法或者其他方法求解驻点，得到x

3 当Mk*p（x）<精确度将此x作为最优解，若不满足将持续增大Mk

（很多算例上直接在算出驻点表达式后，将Mk趋近无穷来求解）

 

内点罚函数法

 做法就是在可行域内部设限制，靠近边缘的域设置较大的障碍，边缘的障碍无穷大，用来解决不等式约束问题，算出的解必在可行域内部

同外点法一样将约束条件转化为函数的一部分，使之成为无约束二次规划问题：

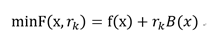
约束条件转化：

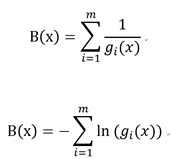
倒数障碍函数和对数障碍函数（使用其中的一种就可以）

算法步骤：和外点法类似，但当前解不满足精度要求时，rk会缩小，甚多算例将rk趋近0来求解函数最小值