数据挖掘-K-近邻算法

数据挖掘-K-近邻算法

目录

K-近邻算法

KNN（K-Nearest Neighbor）最邻近分类算法是数据挖掘分类（classification）技术中最简单的算法之一，其指导思想是”近朱者赤，近墨者黑“，即由你的邻居来推断出你的类别

KNN 算法

思想

为了判断未知样本的类别，以所有已知类别的样本作为参照，计算未知样本与所有已知样本的距离，从中选取与未知样本距离最近的K个已知样本，根据少数服从多数的投票法则（majority-voting），将未知样本与K个最邻近样本中所属类别占比较多的归为一类

KNN在做回归和分类的主要区别，在于最后做预测时候的决策不同

  • 在分类预测时，一般采用多数表决法，即选取的k个邻居中占多数的类
  • 在做回归预测时，一般使用平均值法，即选取的k个邻居中的数值平均值

例：

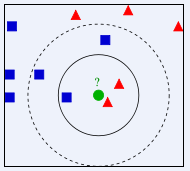
如下图所示，如何判断绿色圆应该属于哪一类，是属于红色三角形还是属于蓝色四方形？

  • 如果K=3，由于红色三角形所占比例为2/3，绿色圆将被判定为属于红色三角形那个类
  • 如果K=5，由于蓝色四方形比例为3/5，因此绿色圆将被判定为属于蓝色四方形类

20180915130853316

特点

由于KNN最邻近分类算法在分类决策时只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合

  • KNN算法即可以应用于分类算法中，也可以应用于回归算法中。

  • KNN算法的准确性很大程度上依赖于K值的选择。

KNN算法涉及的问题

K值的选择

为什么选择K值：KNN算法的准确性很大程度上依赖于K值的选择，要选取合适的K值使得算法最终的结果准确性最高

K值的选择过程：选一个较小的值，然后通过交叉验证选择一个合适的最终值。

k越小，即使用较小的领域中的样本进行预测，训练误差会减小，但模型会很复杂，以至于过拟合。

k越大，即使用交大的领域中的样本进行预测，训练误差会增大，模型会变得简单，容易导致欠拟合。

距离的度量

欧几里得距离

使用欧几里得距离：欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）

  • 在二维和三维空间中的欧氏距离就是两点之间的实际距离
  • 对于n维空间l两点，\(X(x_1,x_2,...x_n),Y(y_1,y_2,...,y_n)\)，两者欧几里得距离：

\(d(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}\)

曼哈顿距离

  • 定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。

    • 例如在平面上，坐标X(x1,x2)的与坐标Y(y1,y2)的曼哈顿距离为：

      \(d(X,Y)=|x_1-y_1|+|x_2-y_2|\)

曼哈顿距离-百度百科

加权KNN算法

KNN算法的不足

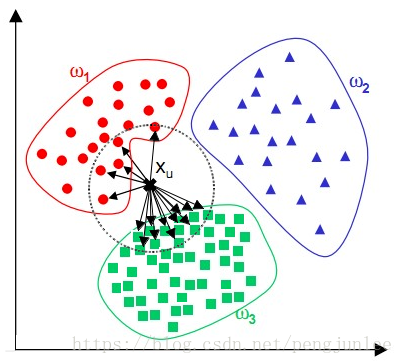
KNN算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时：

  • 该样本的K个邻居中大容量类的样本占多数，如下图所示。该算法只计算最近的邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进

    20180915131206466

加权方式

反函数：

该方法最简单的形式是返回距离的倒数，比如距离d，权重1/d。有时候，完全一样或非常接近的商品权重会很大甚至无穷大。基于这样的原因，在距离求倒数时，在距离上加一个常量：\(weight = \frac{1}{distance + const}\)

这种方法的潜在问题是，它为近邻分配很大的权重，稍远一点的会衰减的很快。虽然这种情况是我们希望的，但有时候也会使算法对噪声数据变得更加敏感。

高斯函数：

\(f(x)=ae^N\),\(N=-\frac{(x-b)^2}{2c^2},a,b,c∈R\)

高斯函数在距离为0的时候权重为1，随着距离增大，权重减少，但不会变为0。

具体算法

在处理离散型数据时，将这k个数据用权重区别对待，预测结果与第n个数据的label相同的概率：

  • \(P_n=\frac{W_n}{\sum_{i=1}^kW_i}\)
  • 例：设有共选取5个最近点，A(1),B(2),C(2),D(2),E(3)（后面为距离,AB属于类1，CDE属于类2），为求简单,设权重为距离的倒数，\(\sum_{i=1}^kW_i=\frac{17}{6}\)，得各权重WA(\(\frac{17}{6}\)),WB(\(\frac{17}{12}\)),WC(\(\frac{17}{12}\)),WD(\(\frac{17}{12}\)),WE(\(\frac{17}{18}\)),则1类的总权重为\(W_1 = \frac{17}{4}=4.25\),\(W_2=\frac{73}{18}=4.0555\),得该点属于1类

在处理数值型数据时，并不是对这k个数据简单的求平均，而是加权平均：通过将每一项的距离值\(D_i\)乘以对应权重\(W_i\)，然后将结果累加。求出总和后，在对其除以所有权重之和,

  • 对于k个点 i类 点的预测结果：
  • \(f(x) = \frac{\sum_{i=1}^kD_iW_i}{\sum_{i=1}^kW_i}\)

每预测一个新样本的所属类别时，都会对整体样本进行遍历，可以看出kNN的效率实际上是十分低下的

加权KNN算法 参考

KNN算法实现

算法步骤

  1. 计算测试数据与各个训练数据之间的距离

  2. 按照距离的递增关系进行排序

  3. 选取距离最小的K个点

  4. 确定前K个点所在类别的出现频率

  5. 返回前K个点中出现频率最高的类别作为测试数据的预测分类

python sklearn包使用

例：

from sklearn.datasets import load_iris
from sklearn.model_selection  import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier

#读取鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31)
k_error = []
#循环，取k=1到k=31，查看误差效果
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    #cv参数决定数据集划分比例，这里是按照5:1划分训练集和测试集
    scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy')
    k_error.append(1 - scores.mean())

#画图，x轴为k值，y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()

sklearn执行KNN算法

posted @ 2020-04-04 10:25  NIShoushun  阅读(785)  评论(0)  编辑  收藏  举报