python调用scikit-learn机器学习
不支持深度学习和强化学习
numpy介绍:
np.eye(n)生成一个n维单元数组
数据预处理:
iris数据加载
|
from sklearn import datasets |
数据展示
显示iris的信息
| print(iris.data) |
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
……
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]]
|
每列数据表示不同样本同一属性下对用的数值
| print(iris.feature_names) |
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] |
输出目标结果
| print(iris.target) |
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] |
结果的含义
| print(iris.target_names) |
['setosa' 'versicolor' 'virginica'] |
确认数据类型
|
print(type(iris.data)) |
<class 'numpy.ndarray'> <class 'numpy.ndarray'> |
确认维度
|
print(iris.data.shape) print(iris.target.shape) |
(150, 4) (150,) |
X输入数据赋值,y输出数据赋值
|
X = iris.data |
模型训练:
分类:根据数据集目标的特征或属性,划分到已有的类别中
常用分类算法:KNN(K近邻)、逻辑回归、决策树、朴素贝叶斯
KNN(最简单的机器学习算法之一):
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的l个实例,这k个实例多数是什么类型就将该输入实例分类到这个类中
模型调用
| from sklearn.neighbors import KNeighborsClassifier |
创建实例
| knn=KNeighborsClassifier(n_neighbors=5) |
模型训练
模型训练与预测
|
y_pred=knn.fit(X,y) |
准确率
|
from sklearn.metrics import accuracy_score |
数据分离
|
from sklearn.model_selection import train_test_split #训练输入数据,预测的输入数据,训练结果,预测结果 |
分离后数据集的训练与评估
|
knn_5_s = KNeighborsClassifier(n_neighbors=5) |
确定k值
|
k_range=list(range(1,26)) score_train=[] |
图形展示
| import matplotlib.pyplot as plt %matplotlib inline #展示k值与训练数据集预测准确率之间的关系 plt.plot(k_range,score_test) plt.xlabel('K(KNN model)') plt.ylabel('Training Accuracy') |
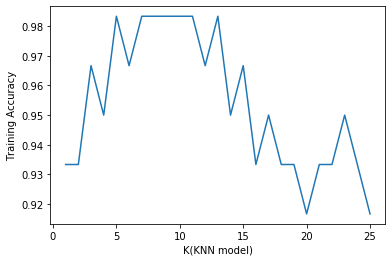
- 训练数据集准确率 随着模型复杂而提高
- 测试数据集准确率 在模型过于简单或复杂而准确率更低
- KNN模型中,模型复杂度由K决定,(k越小,复杂度越高)
对新数据进行预测
|
knn_11=KNeighborsClassifier(n_neighbors=11) |
逻辑回归模型:
用于解决分类问题的一种模型。根据数据特征或属性,计算其归属于每一类别的概率P(x),根据概率数值判断其所属类别。主要应用场景:二分类问题。
P(x)=1/(1+e-(ax+b)) y={1, P(x)≥0.5 0,P(x)<0.5
其中y为类别结果,P为概率,x为特征值,a、b为常量
(皮马印第安人糖尿病数据集)
输入变量:独立变量包括患者的怀孕次数,葡萄糖量,血压,皮褶厚度,体重指数,胰岛素水平,糖尿病谱系功能,年龄
输出结果:是否含义糖尿病
数据来源:Pima Indians Dianbetes dataset
预测准确率的局限性:
无法真实反映模型针对各个分类的预测准确度
准确率可以方便的用于衡量模型的整体预测效果,但无法反应细节信息,具体表现:
- 没有体现数据的实际分布情况
- 没有体现模型错误预测的类型
空准确率:当模型总是预测比例较高的类别,其预测准确率的数值
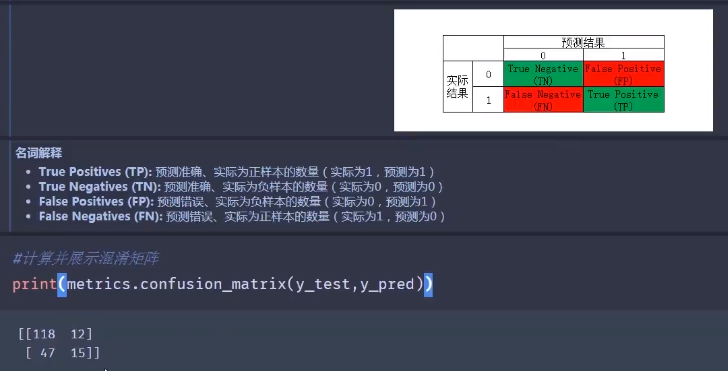
混淆矩阵(误差矩阵):
用于衡量分类算法的准确程度
- True Positives(TP):预测准确、实际为正样本的数量(实际为1,预测为1)
- True Negatives(TN):预测准确、实际为负样本的数量(实际为0,预测为0)
- False Positives(FP):预测错误、实际为负样本的数量(实际为0,预测为1)
- False Negatives(FN):预测错误、实际为正样本的数量(实际为1,预测为0)
| 公式 | 定义 | |
|
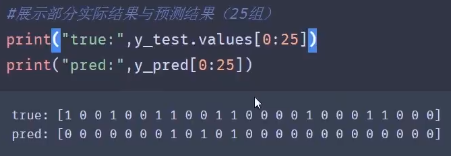
准确率 (Accuracy) |
|
整体样本中,预测正确的比例 |
|
错误率 (Misclassification Rate) |
|
整体样本中,预测错误的比例 |
|
召回率 (Recall) |
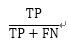 |
正样本中,预测正确的比例 |
|
特异度 (Specificity) |
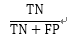 |
负样本中,预测正确的比例 |
|
精确率 (Precision) |
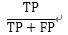 |
预测结果为正样本中,预测正确的比例 |
|
F1分数 (F1 Score) |
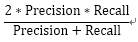 |
综合Precision和Recall的判断指标 |
混淆矩阵指标特点:
- 分类任务中,相比单一的预测准确率,混淆矩阵提供了更全面的模型评估信息
- 通过混淆矩阵,我们可以计算出多样性的模型表现衡量指标,从而更好地选择模型
哪个衡量指标更关键?
- 衡量指标的选择取决于应用场景
- 垃圾邮件检测(正样本判断为“垃圾邮件”):希望普通邮件(负样本)不要被判断为垃圾邮件(正样本),需要关注精确率和召回率
- 异常交易检测(正样本为“异常交易”):希望所有的异常交易都被检测到,需要关注特异度
|
#数据预处理 import pandas as pd path='csv文件路径/xxx.csv' pima=pd.read_csv(path) #X,y赋值 feature_names=['pregnant','insulin','bmi','age'] X=pima[feature_names] y=pima.label #维度确认 print(X.shape,y.shape) #数据分离 from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0) #模型训练 from sklearn.linear_model import LogisticRegression logreg=LogisticRegression() logreg.fit(X_train,y_train) #测试数据集结果预测 y_pred=logreg.predict(X_test) #使用准确率进行评估 from sklearn import metrics print(metrics.accuracy_score(y_test,y_pred)) #确认正负样本数据量 y_test.value_counts() #1的比例 y_test.mean() #0的比例 1-y_test.mean() #空准确率 max(y_test.mean(),1-y_test.mean()) |
|
#四个因子赋值 cofusion=metrics.confusion_matrix(y_test,y_pred) TN=confusion[0,0] FP=confusion[0,1] FN=confusion[1,0] TP=confusion[1,1] print(TN,FP,FN,TP) /*指标计算参见上面的公式*/ |


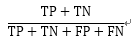
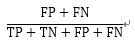

 浙公网安备 33010602011771号
浙公网安备 33010602011771号