Digital root的求解

源于hdu1013

题目描述：

The digital root of a positive integer is found by summing the digits of the integer. If the resulting value is a single digit then that digit is the digital root. If the resulting value contains two or more digits, those digits are summed and the process is repeated. This is continued as long as necessary to obtain a single digit.

For example, consider the positive integer 24. Adding the 2 and the 4 yields a value of 6. Since 6 is a single digit, 6 is the digital root of 24. Now consider the positive integer 39. Adding the 3 and the 9 yields 12. Since 12 is not a single digit, the process must be repeated. Adding the 1 and the 2 yeilds 3, a single digit and also the digital root of 39.

维基百科对digital root的定义：

The digital root (also repeated digital sum) of a non-negative integer is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.

For example, the digital root of 65,536 is 7, because 6 + 5 + 5 + 3 + 6 = 25 and 2 + 5 = 7.

于是老老实实按照题目描述以及定义写了代码：

#include <stdio.h>

#define MAX 8192

char buf[MAX];

int
main(int argc, char **argv)
{
    int i, sum, input;
    
    while (fgets(buf, MAX, stdin)) {
        if (buf[0] == '0' && buf[1] == '\n') {
            break;
        }
        sum = 0;
        input = 0;
        
        for (i = 0; i < MAX; i++) {
            if (buf[i] == '\n') {
                break;
            }
            input += buf[i] - '0';
        }
        
        while ( (input != 0) || (sum / 10 != 0) ) {
            if (input == 0) {
                input = sum;
                sum = 0;
            }
            sum += input % 10;
            input /= 10;
        }
                
        printf("%d\n", sum);
    }
    
    return 0;
}

正确通过。

百度了一下，发现一个关于digital root的结论，一个数字模9同余与各位数位上的和，即n % 9的结果等同于各个数位的和%9。

证明如下：

　　设自然数N=a[n]a[n-1]…a[0]，其中a[0]，a[1]、…、a[n]分别是个位、十位、…上的数字

　　再设M=a[0]+a[1]+…+a[n]

　　求证：N≡M(mod 9).

  　证明：
 　　  ∵ N=a[n]a[n-1]…a[0]=a[n]*10^n+a[n-1]*10^(n-1)+…+a[1]*10+a[0].
 　　 又∵ 1≡1(mod 9),
     　　 10≡1(mod 9),
   　　   10^2≡1(mod 9),
  　　      … 
 　　     10^n≡1(mod 9).
 　　 上面这些同余式两边分别同乘以a[0]、a[1]、a[2]、…、a[n]，再相加得：
 　　　　 a[0]+a[1]*10+…+a[n]*10^n≡(a[0]+a[1]+…+a[n])(mod 9)，
  　　　　　　　　　　　　　　　　  即 N≡M(mod 9)，得证。

这样就能够求解数字n的digital root（下面写作dr）。

分三种情况：

第一，若n=0，则dr=0；

第二，若n != 0, n % 9 = 0，则dr=9；

第三，若n % 9 != 0，则dr = n % 9。

将这三种情况合并，则有公式如下：

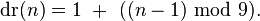
知道了这个结论，我们就很容易编程解决digital root的求解问题了。

 

---

参考：

http://en.wikipedia.org/wiki/Digital_root 维基百科

http://www.cnblogs.com/Rinyo/archive/2012/12/20/2826755.html Rinyo的博客。