P3803 【模板】多项式乘法（FFT）

原题链接

P3811
AC记录：Accepted

题目大意

给定一个 \(n\) 次多项式 \(F(x)\)，和一个 \(m\) 次多项式 \(G(x)\)。
请求出 \(F(x)\) 和 \(G(x)\) 的卷积。

输入格式

第一行两个整数 \(n,m\)。
接下来一行 \(n+1\) 个数字，从低到高表示 \(F(x)\) 的系数。
接下来一行 \(m+1\) 个数字，从低到高表示 \(G(x)\) 的系数。

输出格式

一行 \(n+m+1\) 个数字，从低到高表示 \(F(x) \cdot G(x)\) 的系数。

\(\mathbf{Sample}\) \(\mathbf{Input}\)

1 2
1 2
1 2 1

\(\mathbf{Sample}\) \(\mathbf{Output}\)

1 4 5 2

\(\mathbf{Hint\&Explain}\)
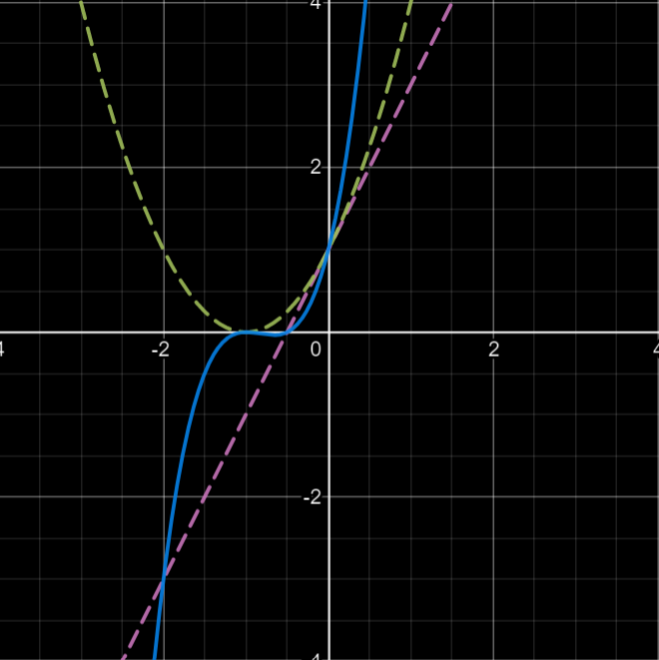
样例如图所示。
其中粉色虚线为 \(F(x)\)，绿色虚线为 \(G(x)\)，蓝色实线为 \(F(x)\cdot G(x)\)。

数据范围

保证输入中的系数大于等于 \(0\) 且小于等于 \(9\)。
对于 \(100\%\) 的数据，\(1 \le n, m \leq {10}^6\)。

解题思路

题目都告诉你了，是用FFT啊。

在介绍FFT之前，你需要知道一些前置的知识。

---

前置知识

\(\texttt{1.}\)复数
复数由两部分组成：实部和虚部。设 \(a,b\) 为实数，\(i=\sqrt{-1}\)，则形如 \(a+bi\) 的数叫做复数。

\(\texttt{2.}\)复数的运算法则
设有两个复数为 \(a+bi\) 和 \(c+di\)。

加法：

\[\begin{matrix} (a+bi)+(c+di) \\[5pt] =a+bi+c+di \\[5pt] =(a+c)+(b+d)i \end{matrix} \]

其实就是把实部和虚部分别相加就可以了。

乘法：

\[\begin{matrix} (a+bi)(c+di) \\[5pt] =ac+adi+bci+bdi^2 \\[5pt] =ac+(ad+bc)i-bds \\[5pt] =(ac-bd)+(ad+bc)i \end{matrix} \]

几何定义：复数相乘，模长相乘，幅角相加。

\(\texttt{Attention : }\)以下内容默认 \(n\) 为 \(2\) 的正整数次幂。

\(\texttt{3.}\)单位根
在复平面（\(x\) 轴代表实部，\(y\) 轴代表虚部）上画一个单位圆（半径为 \(1\) 的圆），以圆点为起点，圆的 \(n\) 等分点为终点，做 \(n\) 个向量，设幅角为正且最小的向量对应的复数为 \(\omega_n\)，称为 \(n\) 次单位根。下图所示的是 \(3\) 次单位根。

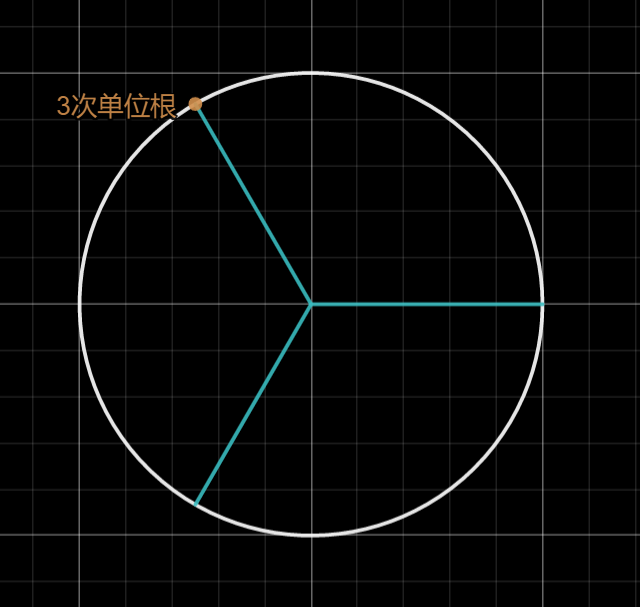
根据复数乘法的运算法则，不难推出剩下的 \(n-1\) 个单位根为 \(\omega^2_n,\omega^3_n,\cdots,\omega^n_n\)。
注意：\(\omega^0_n=\omega^n_n\)。

幅角：假设以逆时针为正方向，从 \(x\) 轴正半轴到已知向量的转角的有向角叫做幅角

\(\texttt{4.}\)单位根的性质

• 由欧拉公式可得，\(\omega^k_n=\cos k\frac{2\pi}{n}+i\sin k\frac{2\pi}{n}\)。
• \(\forall a,\omega^{ak}_{an}=\omega^k_n\)
  证明：

\[\begin{matrix} \omega^{ak}_{an}=\cos ak\cdot\frac{2\pi}{an}+i\sin ak\frac{2\pi}{an} \\[5pt] =\cos k\cdot\frac{2\pi}{n}+i\sin k\frac{2\pi}{n} \\[5pt] =\omega_n \end{matrix} \]

• \(\omega^{k+\frac{n}{2}}_{n}=-\omega^k_n\)
  证明：

\[\begin{matrix} \omega^{k+\frac{n}{2}}_{n}=\omega^k_n\cdot\omega^{\frac{n}{2}}_n \\[5pt] =\omega^k_n\cdot\left(\cos\frac{n}{2}\cdot\frac{2\pi}{n}+i\sin\frac{n}{2}\cdot\frac{2\pi}{n}\right) \\[5pt] =\omega^k_n\cdot\left(\cos\pi+i\sin\pi\right) \\[5pt] =\omega^k_n\cdot(-1) \\[5pt] =-\omega^k_n \end{matrix} \]

接下来，就是重头戏FFT了。

---

快速傅里叶变换（FFT）

设有一个多项式 \(A(x)\)，他的系数为 \((a_0,a_1,a_2,\cdots,a_{n-1})\)。
那么

\[A(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_{n-1}x^{n-1} \]

按照 \(x\) 的次数的奇偶性分类，有

\[A(x)=(a_0+a_2{x^2}+\cdots+a_{n-2}x^{n-2})+(a_1x+a_3{x^3}+\cdots+a_{n-1}x^{n-1}) \]

设

\[A_1(x)=a_0+a_2x+\cdots+a_{n-2}x^{\frac n2-1} \\[5pt] A_2(x)=a_1+a_3x+\cdots+a_{n-1}x^{\frac n2-1} \]

不难得到

\[A(x)=A_1(x^2)+xA_2(x^2) \]

接下来就是把单位根代入了。
但是，不要着急，先把前半部分代进去。
将 \(\omega^k_n(k<\frac n2)\) 代入原式，有

\[A(\omega^k_n)=A_1(\omega^{2k}_n)+\omega^k_nA_2(\omega^{2k}_n) \]

再把后半部分代进去。
将 \(\omega^{k+\frac n2}_n(k<\frac n2)\) 代入原式，有

\[A(\omega^{k+\frac n2}_n)=A_1(\omega^{2\left(k+\frac n2\right)}_n)+\omega^{k+\frac n2}_nA_2(\omega^{2(k+\frac n2)}_n) \\[5pt] =A_1(\omega^{2k+n}_n)-\omega^k_nA_2(\omega^{2k+n}_n) \\[5pt] =A_1(\omega^{2k}_n\cdot\omega^n_n)-\omega^k_nA_2(\omega^{2k}_n\cdot\omega^n_n) \\[5pt] =A_1(\omega^{2k}_n)-\omega^k_nA_2(\omega^{2k}_n) \]

发现没有，这两个式子只有一个常数项不同！
由于 \(k\) 在取遍 \(\left[0,\frac n2-1\right]\) 的时候，\(k+\frac n2\) 取遍了 \(\left[\frac n2,n-1\right]\)。所以，我们在求第一部分的时候，也可以同时求出第二部分的值。
直接把问题缩小了一半！
直接递归求解就好了。
时间复杂度：\(\Theta(n\log_2n)\)。

---

快速傅里叶逆变换（IFFT）

不要以为FFT就结束了。
刚才FFT是基于 点值表示法 的。
但题目里面说的是要 系数表示法 。所以要把点值表示法转换成系数表示法，这个过程就叫 傅里叶逆变换 。
设 \((y_0,y_1,\cdots,y_{n-1})\) 为 \((a_0,a_1,\cdots,a_{n-1})\) 的傅里叶变换（就是点值表示法）。
又设 \((c_0,c_1,\cdots,c_{n-1})\) 为 \((y_0,y_1,\cdots,y_{n-1})\) 在 \((\omega^0_n,\omega^{-1}_n,\cdots,\omega^{-(n-1)}_n)\) 的点值表示，即

\[c_k=\sum_{i=0}^{n-1}y_i(\omega^{-k}_n)^i \\[5pt] =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega^i_n)^j)(\omega^{-k}_n)^i \\[5pt] =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega^j_n)^i(\omega^{-k}_n)^i \\[5pt] =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega^{j-k}_n)^i \\[5pt] =\sum_{j=0}^{n-1}a_j\left(\sum_{i=0}^{n-1}(\omega^{j-k}_n)^i\right) \]

先到这里，让我们换一个地方。
设 \(S(x)=\sum\limits_{i=0}^{n-1}x^i\)。
当 \(k\ne 0\) 时，把 \(\omega^k_n\) 代入得

\[S(\omega^k_n)=1+\omega^k_n+(\omega^k_n)^2+\cdots+(\omega^k_n)^{n-1} \kern{30pt}(1) \]

\((1)\times\omega^k_n\)，得

\[\omega^k_nS(\omega^k_n)=\omega^k_n+(\omega^k_n)^2+\cdots+(\omega^k_n)^n \kern{45pt}(2) \]

\((2)-(1)\)，得

\[\omega^k_nS(\omega^k_n)-S(\omega^k_n)=(\omega^k_n)^n-1 \\[5pt] (\omega^k_n-1)S(\omega^k_n)=(\omega^n_n)^k-1 \\[5pt] S(\omega^k_n)=\frac{(\omega^n_n)^k-1}{\omega^k_n-1} \\[5pt] S(\omega^k_n)=\frac{1-1}{\omega^k_n-1} \\[5pt] S(\omega^k_n)=0 \]

所以，当 \(k\ne 0\) 时，\(S(\omega^k_n)=0\)。
那当 \(k=0\) 时呢？
很显然，当 \(k=0\) 时，\(S(\omega^k_n)=n\)。因为此时 \(\omega^k_n=1\)，而又因为 \(1^n=1,n\in\Z\)，而这样的项共有 \(n\) 项，所以整个式子的值为 \(n\times 1=n\)。

回到原式，继续考虑

\[c_k=\sum_{j=0}^{n-1}a_j\left(\sum_{i=0}^{n-1}(\omega^{j-k}_n)^i\right) \]

由上面的式子可以得出，当 \(j\ne k\) 时，\(\sum\limits_{j=0}^{n-1}(\omega^{j-k}_n)^i=0\)。当 \(j=k\) 时，\(\sum\limits_{j=0}^{n-1}(\omega^{j-k}_n)^i=n\)。因此，

\[c_k=na_k \\[5pt] a_k=\frac1nc_k \]

由于 \((c_0,c_1,\cdots,c_{n-1})\) 为 \((y_0,y_1,\cdots,y_{n-1})\) 在 \((\omega^0_n,\omega^{-1}_n,\cdots,\omega^{-(n-1)}_n)\) 的点值表示，所以相当于又做了一次FFT。

---

迭代实现

尽管你用了上面这么多字之精华写出来了一串代码，但是，你交到洛谷上面去，你还是会\(\texttt{WA }\texttt{77pts}\)。这时候就需要迭代来实现了。
盗用一下某位大佬的图

发现了吗？我们实际上依此操作的元素，实际上就是原来序列的下标的二进制反转得到的！
所以现在的难题就是：如何得到操作后的序列呢？
我们像，对于某个数 \(x\) 来说，他的原序列，是由 \(\frac x2\) 左移一位再加上最后一位的特判得到的。那么在操作后的序列中也一样，他是由 \(\frac x2\) 右移一位再加上最后一位（也就是第一位）的特判得到的。因此，我们就可以在 \(\Theta(n)\) 的时间内求出 \([1,n]\) 操作后的序列所对应的数了。这里给出转移公式：
设数 \(x\) 在 \(k\) 位二进制下操作后的序列所对应的数为 \(r_x\)，有

\[r_x=\left\lfloor\frac{r_{\frac x2}}{2}\right\rfloor+[x\bmod 2=1]\cdot 2^{k-1} \]

其中 \([x]\) 代表当 \(x\) 成立时 \([x]=1\)，不成立时 \([x]=0\)。

上代码

#include<iostream>
#include<cstdio>
#include<cmath>

using namespace std;

struct Complex{
    Complex(double a=0.00,double b=0.00):real(a),imag(b){}
    double real,imag;
};

const double    pi=acos(-1.00);
Complex         a[4000010],b[4000010];
int             resort[4000010];
int             n,m,lim,dig;

Complex operator + (Complex a,Complex b)
{
    return Complex(a.real+b.real,a.imag+b.imag);
}

Complex operator - (Complex a,Complex b) {
    return Complex(a.real-b.real,a.imag-b.imag);
}

Complex operator * (Complex a,Complex b)
{
    double real,imag;
    real=a.real*b.real-a.imag*b.imag;
    imag=a.real*b.imag+a.imag*b.real;
    return Complex(real,imag);
}

void FFT(Complex *c,int state)
{
    for(int i=0; i<lim; i++)
        if(i<resort[i])
            swap(c[i],c[resort[i]]);
    for(int i=1; i<lim; i<<=1)
    {
        Complex W1n(cos(pi/i),state*sin(pi/i));
        for(int Size=i<<1,j=0; j<lim; j+=Size)
        {
            Complex W(1.00,0.00);
            for(int k=0; k<i; k++,W=W*W1n)
            {
                Complex x=c[j+k],y=W*c[j+i+k];
                c[j+k]=x+y;
                c[j+i+k]=x-y;
            }
        }
    }
    return;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    /* Code */
    cin>>n>>m;
    for(int i=0; i<=n; i++)
        cin>>a[i].real;
    for(int i=0; i<=m; i++)
        cin>>b[i].real;
    lim=1,dig=0;
    while(lim<=n+m)
        lim<<=1,dig++;
    for(int i=0; i<lim; i++)
        resort[i]=(resort[i>>1]>>1)|((i&1)<<(dig-1));
    FFT(a,1);
    FFT(b,1);
    for(int i=0; i<lim; i++)
        a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0; i<=n+m; i++)
        cout<<(int)(a[i].real/lim+0.5)<<" ";
    return 0;
}