基数排序的一个变形应用

    说起排序，大多数人在实际项目中很少自己去写一个排序，一般来说，qsort一行话就可以了。我也很少在实际项目中用到过基数排序，最近，写了一篇博客文章叫做： 字符串之全文索引 ，这篇文章的下一篇文章 要用到一个倍增算法。这个倍增算法，就可以非常巧妙的运用基数排序。作为那篇文章的一个铺垫，我专门写了一篇基数排序的文章。这篇文章里面的基数排序肯定是一个变形。

大多数网上 或者 书上的基数排序都是从下面的例子开始的：

排序下面的数列：

73  22  93  43  55  14  28  65  39  81

然后对这些数字，用个位数进行排序：

0
1	81
2	22
3	73	93	43
4	14
5	55	65
6
7
8	28
9	39

从这个二维的数组里面顺序取出：

81 22 73 93 43 14 55 65 28 39

 

再对10位数进行排序：

0
1	14
2	22	28
3	39
4	43
5	55	65
6
7	73
8	81
9	93

 

从这个二维数组里面顺序取出：

14 22 28 39 43 55 65 73 81 93

上面的思路写成代码也非常的容易写：

#include <stdio.h>
#include <stdlib.h>
int main()
{
    int data[10]={73,22,93,43,55,14,28,65,39,81};
    int temp[10][10]= {0};
    int order[10]={0};
    int i,j,k,n,lsd;

    printf("\n排序前: ");
    for (i=0; i<10; i++) printf("%d ",data[i]);
    putchar('\n');
    n=1;
    while (n<=10)
    {
        for (i=0;i<10;i++)
        {
            lsd=((data[i]/n)%10);
            temp[lsd][order[lsd]]=data[i];
            order[lsd]++;
        }
        printf("\n重新排列: ");
        k = 0;
        for (i=0;i<10;i++)
        {
            if(order[i]!=0)
            {
                for (j=0;j<order[i];j++)
                {
                    data[k]=temp[i][j];
                    printf("%d ",data[k]);
                    k++;
                }
                order[i]=0;
            }
        }
        n *= 10;
    }
    putchar('\n');
    printf("\n排序后: ");
    for (i=0; i<10; i++) printf("%d ",data[i]);
    return 0;
}

既然这个基数排序理论上性能比较的高，这样的话，我们就写个程序比较一下实际上快速排序和基数排序的速度。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <algorithm>

#define MAX_N 5000000
int sort[10][MAX_N];
int data[MAX_N];
int data2[MAX_N];
int data3[MAX_N];
int radix_sort(int data[], int max_index, int max_number);
static int range_rand(int min, int max);

int intcmp(const void *a, const void *b)
{
    return *((int *)a) - *((int *)b);
}

int main()
{
    int i;
    int max = -1;
    clock_t t;
    for (i = 0; i < MAX_N; i++)
    {
        data[i] = range_rand(1, 0xFFFFFFF);
        if (max < data[i]) max = data[i];
    }
    memcpy(data2, data, sizeof(data));
    memcpy(data3, data, sizeof(data));
    t = clock();
    qsort(data, MAX_N, sizeof(int), intcmp);
    printf("qsort cost : %d \n", clock() - t);

    t = clock();
    radix_sort(data2, MAX_N, max);
    printf("radix cost : %d \n", clock() - t);

    t = clock();
    std::sort(data3, data3 + MAX_N);
    printf("std::sort cost : %d \n", clock() - t);

    for (i = 0; i < 20; i++)
    {
        printf("%d ", data[i]);
    }
    printf("\n");
    for (i = 0; i < 20; i++)
    {
        printf("%d ", data2[i]);
    }
    printf("\n");

    for (i = 0; i < 20; i++)
    {
        printf("%d ", data3[i]);
    }
    printf("\n");
}

int radix_sort(int data[], int max_index, int max_number)
{

    int number[10];
    int lsd, i, k, j, n;
    n = 1;
    memset(number, 0, sizeof(number));
    while (n <= max_number)
    {
        for (i = 0; i < max_index; i++)
        {
            lsd = (data[i]/n) % 10;
            sort[lsd][number[lsd]] = data[i];
            number[lsd]++;
        }
        k = 0;
        for (i = 0; i < 10; i++)
        {
            if(number[i] != 0)
            {
                for (j = 0; j < number[i];j++)
                {
                    data[k] = sort[i][j];
                    k++;
                }
                number[i] = 0;
            }
        }
        n *= 10;
    }
    return 0;
}

static int range_rand(int min, int max)
{
    double r = 0;
    int    i;
    double mul = 1;
    for (i = 0; i < 3; i++)
    {
        mul *= 0.0001;
        r += (rand() % 10000) * mul;
    }
    //0 - 1 中的一个随机数
    return (int)(r * (max - min)) + min;
}

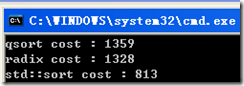
我用了500万数据进行测试，在我电脑上的运行结果是：

你会发现C++ stl 里面的sort 是最快的（没有函数调用的损失）。radix sort  和 qsort 性能差不多。所以，在某个数字可能很大的时候，上面的这个算法没有任何性能上的优势，还会浪费非常多的内存。

 

基数排序大多数情况下面只适用于下面的情景，一组数，这组数的最大值不是很大，更加准确的说，是要排序的对象的数目 和 排序对象的最大值之间相差不多。比如，这组数 1 4 5 2 2，要排序对象的数目是 5 ，排序对象的最大值也是 5. 这样的情况很适合。我们原来的排序的数，默认是以10为基数，现在，这个改进算法是这样的，我以最大的那个数为基数，这样，所有的数都是“个位数”，问题就简单了。

说了这样多，我觉得还是用程序来表达比较的清晰：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <algorithm>

#define MAX_N 5000000

int sort[10][MAX_N];
int quick_radix_sort[MAX_N];
int data[MAX_N];
int data2[MAX_N];
int data3[MAX_N];
int data4[MAX_N];

int qradix_sort(int data[], int max_index);
int radix_sort(int data[], int max_index, int max_number);
static int range_rand(int min, int max);

int intcmp(const void *a, const void *b)
{
    return *((int *)a) - *((int *)b);
}

int main()
{
    int i;
    int max = -1;
    clock_t t;
    //初始化随机数种子
    srand ( time(NULL) );
    for (i = 0; i < MAX_N; i++)
    {
        data[i] = range_rand(1, MAX_N - 1);
        if (max < data[i]) max = data[i];
    }
    memcpy(data2, data, sizeof(data));
    memcpy(data3, data, sizeof(data));
    memcpy(data4, data, sizeof(data));

    t = clock();
    qsort(data, MAX_N, sizeof(int), intcmp);
    printf("qsort cost : %d \n", clock() - t);

    t = clock();
    radix_sort(data2, MAX_N, max);
    printf("radix cost : %d \n", clock() - t);

    t = clock();
    std::sort(data3, data3 + MAX_N);
    printf("std::sort cost : %d \n", clock() - t);

    t = clock();
    qradix_sort(data4, MAX_N);
    printf("quick radix sort cost : %d \n", clock() - t);

    for (i = 0; i < 20; i++)
    {
        printf("%d ", data[i]);
    }
    printf("\n");
    for (i = 0; i < 20; i++)
    {
        printf("%d ", data2[i]);
    }
    printf("\n");

    for (i = 0; i < 20; i++)
    {
        printf("%d ", data3[i]);
    }
    printf("\n");

    for (i = 0; i < 20; i++)
    {
        printf("%d ", data4[i]);
    }
    printf("\n");

}

int qradix_sort(int data[], int max_index)
{
    int i, j, n = 0;
    for (i = 0; i < max_index; i++)
    {
        quick_radix_sort[data[i]]++;
    }
    for (i = 0; i < max_index; i++)
    {
        for (j = 0; j < quick_radix_sort[i]; j++)
        {
            data[n++] = i;
        }
    }
    return 0;
}

int radix_sort(int data[], int max_index, int max_number)
{

    int number[10];
    int lsd, i, k, j, n;
    n = 1;
    memset(number, 0, sizeof(number));
    while (n <= max_number)
    {
        for (i = 0; i < max_index; i++)
        {
            lsd = (data[i]/n) % 10;
            sort[lsd][number[lsd]] = data[i];
            number[lsd]++;
        }
        k = 0;
        for (i = 0; i < 10; i++)
        {
            if(number[i] != 0)
            {
                for (j = 0; j < number[i];j++)
                {
                    data[k] = sort[i][j];
                    k++;
                }
                number[i] = 0;
            }
        }
        n *= 10;
    }
    return 0;
}

static int range_rand(int min, int max)
{
    double r = 0;
    int    i;
    double mul = 1;
    for (i = 0; i < 3; i++)
    {
        mul *= 0.0001;
        r += (rand() % 10000) * mul;
    }
    //0 - 1 中的一个随机数
    return (int)(r * (max - min)) + min;
}

 

这个代码其实就是在上面的测试代码的基础上加上了一个qradix_sort 函数，这个函数非常的简单：

int qradix_sort(int data[], int max_index)
{
    int i, j, n = 0;
    for (i = 0; i < max_index; i++)
    {
        quick_radix_sort[data[i]]++;
    }
    for (i = 0; i < max_index; i++)
    {
        for (j = 0; j < quick_radix_sort[i]; j++)
        {
            data[n++] = i;
        }
    }
    return 0;
}

循环体里面就两句话，和我们前面的那个基数排序不是很一样，这里，已经不用一个二维数组保存排序的数字了，只是标记一下这个数字有几个，因为，下标其实就是被排序的数字。

重新排序这个循环也很简单，仔细冥想一下怎么回事，不懂就在草稿纸上画画草图吧。这里主要的思想还是，下标就是排序的数字。

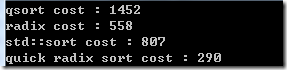
最后的排序测试结果：

我们发现，现在普通的radix性能也提高了，因为，现在数字变小了，循环的次数也变少了。快速基数排序的性能提高还是非常的明显。普通基数排序的两倍，std::sort 的3倍，qsort的 5倍，最重要的是代码非常的简单，基本上是你见过的最简单的一个排序了。

 

对一个真正的程序员来说，很少这样要死抠一个程序的性能，一般情况下，也是得不偿失。只有，在某个东西真正成了一个性能瓶颈的时候，我们才需要去关心一下：是不是可以这样改进一下。

 

这个排序算法，将来会应用到 字符串处理的倍增算法里面，这个倍增算法，要反复的进行排序。如果，排序能快一点，这个程序就能快很多。