算法刷了也有小400了,该静下心来好好总结一下了
这个针对于求链表的中点等一些很有用
//伪代码
//求链表的中间节点[1,2,3]就是2;[1,2,3,4]就是3
public ListNode getMidListNode(ListNode root){
if(root==null||root.next==null)return root;
ListNode slowPoint=root;
ListNode fastPoint=root;
while(fastPoint.next!=null&&fastPoint.next.next!=null){
slowPoint=slowPoint.next;
fastPoint=fastPoint.next.next;
}
if(fastPoint.next!=null){
slowPoint=slowPoint.next;
}
return slowPoint;
}
2.求和为k的连续子序列
技巧就是用HashMap接收前面已经存在的值了
例1(LC1):求两个和为k的值的下标
我们可以在遍历的时候,使用HashMap来接收当前值为key,和他当前的索引i为value,然后每次走的时候只需要判断当前hashmap中存不存在k-nums[i],如果存在答案就出来了//伪代码如下
public int get2Add(int nums[],int k){
HashMap<Integer,Integer> hashMap=new HashMap<>();
int res[]=new int[2];
for(int i=0;i<nums.length;i++){
if(hashMap.contains(k-nums[i])){
res[0]=hashMap.get(k-nums[i]);
res[1]=i;
}
else{
hashMap.put(nums[i],i);
}
}
return res;
}例2(也是LC):求和为k的连续子序列的个数
当我们走到当前位置,将当前位置的和(从头开始的)记录下来,如果j~i之间的和为k,也就是说pre[i]-pre[j-1]=k,转化一下就是pre[i]-k=pre[j-1];也就是说如果hashMap中有pre[j-1],就说明存在从j到i的子串,他们前面的和为pre[j-1],也就是j~i和为k//伪代码
public int getCount(int nums[],int k){
HashMap<Integer,Integer> hashMap=new HashMap<>();
hashMap.put(0,1);//针对于某个值正好等于k
int sum=0;
int res=0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
if(hashMap.contains(sum-k)){
res+=hashMap.get(sum-k);
}
hashMap.put(hashMap.getOrDefault(sum,0)+1) ;
}
return res;
}
3.滑动窗口
这个我博客有很好的总结,大体的流程一定是这样:
int l=0,r=0;
while(r<len){
//do something...
if(判断条件){
//do something...
}
else{
//需要移动左指针
}
r++;
}按照这个思路来写,滑动窗口就不会有问题。
4.最长回文串
就是从中心出发,向两边扩散,当然还有奇偶,因此一次循环的时候,两个都考虑,把最大的留下来即可。
//伪代码
//截取字符串太浪费性能了,我们期间不截取,我们找到最大的之后,把左右指针位置保存下来,最后返回的时候截取一次就好了
public String getMaxLenPastr(String s){
if(s==null|s.length()<=1)return s;
int len=s.length();
int oddl,oddr,evenl,evenr;//奇数和偶数的左右指针
int maxl=0,maxr=0,max=0;
int templ,tempr;
for(int i=0;i<len-1;i++){//最后一位最多就是1,因此不需要考虑它
//先考虑单个中心的扩散(下方代码我们停留的位置内部是回文串,也就是到了我们停留位置就不满足了,这个要知道)
oddl=i;
oddr=i;
while(oddl>=0&&oddr<len){
if(s.charAt(oddl)!=s.charAt(oddr))break;
oddl--;
oddr++;
}
//再考虑两个为中心的中心扩散
evenl=i;
evenr=i+1;
while(evenl>=0&&evenr<len){
if(s.charAt(evenl)!=s.charAt(evenr))break;
evenl--;
evenr++;
}
if(oddr-oddl>evenr-evenl){
templ=oddl;
tempr=oddr;
}
else{
templ=evenl;
tempr=evenr;
}
//tempr-templ+1-2
if(tempr-templ-1>max){
max=tempr-templ-1;
maxl=templ+1;
maxr=tempr;
}
}
return s.substring(maxl,maxr);
}
5.二叉树的遍历(非递归)
我的博客也有
(有一个很有意思的点,当我们使用栈来做的时候,我们会发现无论哪种遍历,我们都会首先将根节点加进去,这个很有趣) 有点像BFS在使用队列的时候一样,我们总是首先将根节点加入进去
前序遍历
public List<Integer> preOder(TreeNode root){
List<Integer> res=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
if(root!=null)
stack.push(root);
TreeNode curNode;
while(!stack.isEmpty()){
curNode=stack.pop();
res.add(curNode.val);
if(curNode.right!=null)stack.push(curNode.right);
if(curNode.left!=null)stack.push(curNode.left);
}
return res;
}中序遍历(有左边压左边,如果没有弹出,从它做文章)
public List<Integer> infixOrder(TreeNode root){
List<Integer> res=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
if(root!=null)
stack.push(root);
TreeNode curNode=root;
while(!stack.isEmpty()){
if(curNode!=null&&curNode.left!=null){
stack.push(curNode.left);
curNode=curNode.left;
}
else{
curNode=stack.pop();
res.add(curNode.val);
if(curNode!=null&&curNode.right!=null){
stack.push(curNode.right);
curNode=curNode.right;
}
else{
curNode=null;
}
}
}
return res;
}后序遍历
public List<Integer> sufixOrder(TreeNode root){
LinkedList<Integer> res=new LinkedList<>();
Stack<TreeNode> stack=new Stack<>();
if(root!=null)
stack.push(root);
TreeNode curNode=root;
while(!stack.isEmpty()){
curNode=stack.pop();
res.addFirst(curNode.val);
if(curNode.left!=null)stack.push(curNode.left);
if(curNode.right!=null)stack.push(curNode.right);
}
return res;
}
6.双指针
左右两个指针,一个往左,一个往右,这个在有序里面用到还是很多的,比如说LC中找【三数之和】
LC三数之和为k(注意去重):
//伪代码
//思路也就是:固定一个,然后其余两个双指针即可
public List<List<Integer>> getRes(int nums[],int k){
List<List<Integer>> res=new ArrayList<>();
Arrays.sort(nums);
int l,r,sum;
int len=nums.length;
for(int i=0;i<len;i++){
if(nums[i]>k)break;//第一个都比k大,那和不可能比k小了
if(i>0&&nums[i]==nums[i-1])continue;
l=i+1;
r=len-1;
while(l<r){
sum=nums[i]+nums[l]+nums[r];
if(sum<k){
l++;
}
else if(sum>k){
r--;
}
else{
res.add(Arrays.asList(nums[i],nums[l],nums[r]));
while(l<r&&nums[l]==nums[l+1])l++;
while(l<r&&nums[r]==nums[r-1])r--;
l++;
r--;
}
}
}
return res;
}
7.反转链表
//伪代码
ListNode res=null;
ListNode next;
while(head!=null){
next=head.next;
head.next=res;
res=head;
head=next;
}
8.leetcode 原题链接:跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
输入: [2,3,1,1,4] 输出: true 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
public boolean canJump(int[] nums) {
int max=0;
for(int i=0;i<nums.length;i++){
if(i>max)return false;
max=Math.max(max,i+num[i]);
}
return true;
}
9.约瑟夫环问题
这题我们可以使用循环链表来做,这种方式我自己从0写,至少写了5遍了,每次都写好长好长的代码,直到我看到了这个思路:
(思路就是倒叙推,最后一个剩余的元素只有一个那么他的索引就是0,上一层就有2个元素,这个元素的位置在(0+m)%2,这个值作为新的index,继续找(index+m)%3...一直找到第n层即可,显然找到列表有n的元素的位置的时候就是这个剩余的元素所处的位置)
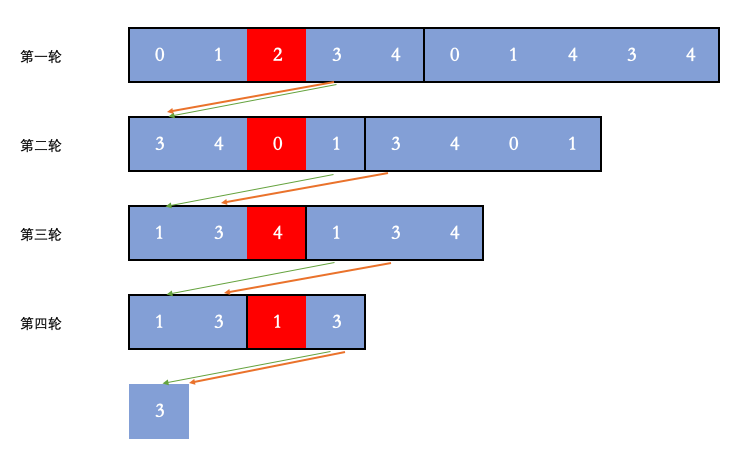
数学解法,O(n)O(n) 这么著名的约瑟夫环问题,是有数学解法的! 因为数据是放在数组里,所以我在数组后面加上了数组的复制,以体现是环状的。我们先忽略图片里的箭头: 【第一轮后面的数字应该是[0, 1, 2 ,3 ,4],手误打错了。。抱歉】
很明显我们每次删除的是第 mm 个数字,我都标红了。
第一轮是 [0, 1, 2, 3, 4] ,所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。
第二轮开始时,从 3 开始,所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。
第三轮开始时,从 1 开始,所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。
第四轮开始时,还是从 1 开始,所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。
最后剩下的数字是 3。
图中的绿色的线指的是新的一轮的开头是怎么指定的,每次都是固定地向前移位 mm 个位置。
然后我们从最后剩下的 3 倒着看,我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推,补上 mm 个位置,然后模上当时的数组大小 22,位置是(0 + 3) % 2 = 1。
第三轮反推,补上 mm 个位置,然后模上当时的数组大小 33,位置是(1 + 3) % 3 = 1。
第二轮反推,补上 mm 个位置,然后模上当时的数组大小 44,位置是(1 + 3) % 4 = 0。
第一轮反推,补上 mm 个位置,然后模上当时的数组大小 55,位置是(0 + 3) % 5 = 3。
所以最终剩下的数字的下标就是3。因为数组是从0开始的,所以最终的答案就是3。
总结一下反推的过程,就是 (当前index + m) % 上一轮剩余数字的个数。
代码就很简单了。
class Solution {
public int lastRemaining(int n, int m) {
int ans = 0;
// 最后一轮剩下2个人,所以从2开始反推
for (int i = 2; i <= n; i++) {
ans = (ans + m) % i;
}
return ans;
}
}
10.LC312(戳气球获得最大金币)
dp[i][j]:i~j之间能产生的最大值 【1~n就是我们需要寻找的】
我们假设在i~j之间最后取出的是k,则我们有如下算式
dp[i][j]=dp[i][k-1]+dp[k+1][j]+pointer[i-1]*pointer[k]*pointer[j+1]上式的解释:因为k是最后一个扎破的气球,因此计算
i~k-1与k+1~j,它的得分就是pointer[i-1]*pointer[k]*pointer[j+1]
还有一点遍历之所以自下向上,自左向右,这个是根据我们的状态转移方程的哦,这个要牢记
因为i<=k<=j,所以
dp[i][k-1]在二维表dp[i][j]的左边,因此我们的列需要从左向右
dp[k+1][j]在二维表dp[i][j]的下边,因此我们的行需要从下向上
public int maxCoins(int[] nums) {
int n=nums.length;
int[] pointer=new int[n+2];
pointer[0]=1;
pointer[n+1]=1;
for (int i = 1; i <= n; i++) {
pointer[i]=nums[i-1];
}
//dp[i][j]代表i~j可以得到的最大金币
int[][] dp=new int[n+2][n+2];
for(int i=n;i>0;i--){
for(int j=i;j<n+1;j++){
for(int k=i;k<=j;k++){//k是最后取出的一个(这个点是这道题的关键)
dp[i][j]=Math.max(dp[i][j],
dp[i][k-1]+dp[k+1][j]+pointer[i-1]*pointer[k]*pointer[j+1]);
}
}
}
return dp[1][n];
}
我的博客
11.LC452(戳气球)
这道题不难,我们只需要按照结尾排序,这样我们确保了下一个的气球结尾一定比我大,我只需要判断它初始位置是不是<=我当前的位置,如果是则他也就能被扎破了,否则必须从它开始(因为这是下一个结尾最小的了)
public int findMinArrowShots(int[][] points) {
if(points==null||points.length==0)return 0;
Arrays.sort(points,(o1,o2)->o1[1]-o2[1]);
int res=1;
int curMax=points[0][1];
for(int[] item:points){
if(item[0]>curMax){
res++;
curMax=item[1];
}
}
return res;
}
12.最少插眼个数
这道题显然和上方还是有区别的,为我们需要插入一个范围,因此我们不能按照结尾排序了,需要按照开头排。
思路就是:1.从起点开始找满足的重点最大;2.若出现>起点了,判断是不是比起点的终点还大,如果是则不连续,如果不是则以此时最大的终点为起点继续寻找。
import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner s=new Scanner(System.in);
while (s.hasNext()){
int n=s.nextInt();
int L=s.nextInt();
int[][] arr=new int[n][2];
for (int i = 0; i < n; i++) {
arr[i][0]=s.nextInt();
arr[i][1]=s.nextInt();
}
Arrays.sort(arr, Comparator.comparingInt(o -> o[0]));
int l=0,r=0,res=0;
for(int[] item:arr){
if(item[0]<=l){
r=Math.max(r,item[1]);//找到可延伸最大的
if(r>=L){
res++;
System.out.println(res);
return;
}
}
else{
if(item[0]>r){//最左区间都不在r内,那么不连续
System.out.println(-1);
return;
}
res++;
l=r;
r=item[1];
if(r>=L){
res++;
System.out.println(res);
return;
}
}
}
if(r<L) System.out.println(-1);//找到最后最长的区间,长度也不足L
}
}
}
//这个写法
public int getMinCount(int arrs[][],int L){
Arrays.sort(arr,Comparator.comparingInt(o -> o[0]));
int l=0,r=0,res=1;
for(int[] item:arrs){
if(item[0]<=l){
r=Math.max(r,item[1]);
if(r>=L)return res;
}
else{
if(item[0]>r){
return -1;
}
res++;
l=r;
r=item[1];
if(r>=L)return res;
}
}
if(r<L) return -1
return res;
}
13.双指针问题(很巧)
题目:给定一个有序数组,请算出平方后的结果可能的个数。
思路一:计算平方然后排序,然后找(o(nlogn))
思路二:双指针(o(n))【取完绝对值后,我们只需要每次找到相同的最末端就好(左在右端,右在左端);如:3 【3】0 1【2】2 】
//统计数组的数字平方和不同的个数
//利用双指针
public int findElements(int[] arr){
int len=arr.length;
for(int i=0;i<len;i++){
arr[i]=Math.abs(arr[i]);
}
int l=0,r=len-1;
int count=0;
while(l<=r){
//找到第一个相等的数字的端(左在右端,右在左端)
while(l<r&&arr[l]==arr[l+1]){
l++;
}
while(l<r&&arr[r]==arr[r-1]){
r--;
}
if(arr[l]<arr[r]){
r--;
}
else if(arr[l]>arr[r]){
l++;
}
else{
r--;
l++;
}
count++;
}
return count;
}
14.双指针问题(2)
题目:
一个数据先递增再递减(可能包含重复的数字【也就是说不是严格的递增】),找出数组不重复的个数。不能使用额外空间,复杂度o(n)
public int findElements(int[] arr){
int count=0;
int l=0,r=arr.length-1;
while(l<=r){
//找到端
while(l<r&&arr[l]==arr[l+1]){
l++;
}
while(l<r&&arr[r]==arr[r-1]){
r--;
}
if(arr[l]<arr[r]){
l++;
}
else if(arr[l]>arr[r]){
r--;
}
else{
l++;
r--;
}
count++;
}
return count;
}
15.每k个反转一次链表
//每k个反转一次链表
//https://leetcode-cn.com/problems/reverse-nodes-in-k-group/
//以下为自己写的代码,效率极高 超过lc 100%java用户
public ListNode reverseKGroup(ListNode head, int k) {
//首先需要判断够不够k个
boolean isOk=true;
ListNode test=head;
for(int i=0;i<k;i++){
if(test==null){
isOk=false;
break;
}
test=test.next;
}
if(!isOk){
return head;
}
ListNode res=null;
ListNode next=null;
ListNode tail=head; //保存每个的尾部,因为在翻转的时候,最开始的会变成尾部,我使用尾部连接就好啦
//先翻转前k个
for(int i=0;i<k;i++){
next=head.next;
head.next=res;
res=head;
head=next;
}
tail.next=reverseKGroup(head,k);
return res;
}
16.顺时针打印数组(面试笔试最常考之一)
public List<Integer> printClockWise(int[] arr){
List<Integer> res=new ArrayList<>();
if(arr==null||arr.length==0||arr[0].length==0)return res;
int l=0,r=arr[0].length-1,t=0,b=arr.length-1;
while(true){
for(int i=l;i<=r;i++){
res.add(arr[t][i]);
}
if(++t>b)break;
for(int i=t;i<=b;i++){
res.add(arr[i][r]);
}
if(--r<l)break;
for(int i=r;i>=l;i--){
res.add(arr[b][i]);
}
if(--b<t)break;
for(int i=b;i>=t;i--){
res.add(arr[i][l]);
}
if(++l>r)break;
}
return res;
}
17.数组排序
写一下堆排序,归并排序,快速排序,插入排序,冒泡排序
堆排序:重点就是adjustHeap这个调整堆的函数
我们首先需要调整堆,最初的时候是完全无序的,因此第一次我们需要从后往前调整堆((len-1-1)/2)
堆形成后,我们将堆首与最后一个叶子节点交换,然后我们移除这个叶子节点,这样一直下去我们就可以通过堆完成排序了
//heap sort
public void heapSort(int[] arr){
int len=arr.length;
for(int i=len/2-1;i>=0;i--){
adjustHeap(arr,i,len);
}
for(int i=len-1;i>0;i--){
swap(arr,0,i);
adjustHeap(arr,0,i);
}
}
//重点就是调整堆的这个函数
//arr是数组,i是从哪个元素开始调整堆,lenth是当前数组从0开始考虑的长度
private void adjustHeap(int arr[],int i,int length){
int temp=arr[i];
for(int k=2*i+1;k<length;k=2*k+1){
//首先判断右节点是不是比左节点还要大,因为我们要找最大的
if(k+1<length&&arr[k+1]>arr[k]){
k++;
}
if(arr[k]>temp){
arr[i]=arr[k];
i=k;
}
else{
break;
}
}
arr[i]=temp;
}
private void swap(int[] arr,int a,int b){
int temp=arr[a];
arr[a]=arr[b];
arr[b]=temp;
}
归并排序:先拆数组,然后合并
public void mergeSort(int[] arr){
int[] temp=new int[arr.length];
mergeSort(arr,0,arr.length-1,temp);
}
private void mergeSort(int[] arr,int leftIndex,int rightIndex,int[] temp){
if(leftIndex>=rightIndex)return;
int mid=(leftIndex+rightIndex)/2;
mergeSort(arr,leftIndex,mid,temp);
mergeSort(arr,mid+1,rightIndex,temp);
int l=mid,r=rightIndex,t=rightIndex;
while(l>=leftIndex&&r>mid){
if(arr[l]>=arr[r]){
temp[t--]=arr[l--];
}
else{
temp[t--]=arr[r--];
}
}
while(l>=leftIndex){
temp[t--]=arr[l--];
}
while(r>mid){
temp[t--]=arr[r--];
}
for(int i=leftIndex;i<=rightIndex;i++){
arr[i]=temp[i];
}
}
快速排序:固定最左边,然后指针先从右找,找到停下,然后左指针再找,找到交换一直到l==r停止,此时左边都是<=base右边都是>base所以我们针对于左右再排序就好了
public void quickSort(int[] arr){
quickSort(arr,0,arr.length-1);
}
private void quickSort(int[] arr,int leftIndex,int rightIndex){
if(leftIndex>=rightIndex)return;
int base=arr[leftIndex];
int l=leftIndex,r=rightIndex;
while(l<r){
while(l<r&&arr[r]>base){
r--;
}
while(l<r&&arr[l]<=base){
l++;
}
//交换
swap(arr,l,r);
}
arr[leftIndex]=arr[l];
arr[l]=base;
quickSort(arr,leftIndex,l-1);
quickSort(arr,l+1,rightIndex);
}
private void swap(int[] arr,int a,int b){
int temp=arr[a];
arr[a]=arr[b];
arr[b]=temp;
}
插入排序:
public void insertSort(int[] arr){
int insertVal,insertIndex;
for(int i=0;i<arr.length;i++){
insertVal=arr[i];
insertIndex=i-1;
while(insertIndex>=0&&arr[insertIndex]>insertVal){
arr[insertIndex+1]=arr[insertIndex];
insertIndex--;
}
arr[insertIndex+1]=insertVal;
}
}public void insertSort(int[] arr){ for(int i=1;i<arr.length;i++){ for(int j=i;j>0;j--){ if(arr[j-1]>arr[j]){ swap(arr,j-1,j); } } } }
冒泡排序:每次将最大的移到最后
public void bubbleSort(int[] arr){
for(int i=arr.length-1;i>0;i--){
for(int j=0;j<i;j++){
if(arr[j]>arr[j+1]){
swap(arr,j,j+1);
}
}
}
}
private void swap(int[] arr,int a,int b){
int temp=arr[a];
arr[a]=arr[b];
arr[b]=temp;
}public void bubbleSort(int[] arr){
for(int i=0;i<arr.length;i++){
for(int j=0;j<arr.length-1-i;j++){
if(arr[j]>arr[j+1]){
swap(arr,j,j+1);
}
}
}
}
18.LC845数组中的最长山脉
我们把数组 A 中符合下列属性的任意连续子数组 B 称为 “山脉”:
B.length >= 3 存在 0 < i < B.length - 1 使得 B[0] < B[1] < ... B[i-1] < B[i] > B[i+1] > ... > B[B.length - 1] (注意:B 可以是 A 的任意子数组,包括整个数组 A。)
给出一个整数数组 A,返回最长 “山脉” 的长度。
如果不含有 “山脉” 则返回 0。
输入:[2,1,4,7,3,2,5]
输出:5
解释:最长的 “山脉” 是 [1,4,7,3,2],长度为 5。
class Solution {
public int longestMountain(int[] arr) {
if(arr==null||arr.length==0) return 0;
int len=arr.length;
int res=0,index=0;
while(index<len){
int end=index;
//先升序
if(end+1<len&&arr[end]<arr[end+1]){
while(end+1<len&&arr[end]<arr[end+1]){
end++;
}
//再降序,才是山脉
if(end+1<len&&arr[end]>arr[end+1]){
while(end+1<len&&arr[end]>arr[end+1]){
end++;
}
res=Math.max(res,end-index+1);
}
}
index=Math.max(index+1,end);
}
return res;
}
/*
//动态规划运行到72/72超时。。。。
if(arr==null||arr.length==0)return 0;
int n=arr.length;
int res=0;
boolean[][] dp=new boolean[n][n];//代表i~j是否是山脉
//dp[i][j]=(j-i+1>=3)&&dp[i+1][j-1]&&arr[i]<arr[i+1]&&arr[j]<arr[j-1]
//上方的表达式其实还是有问题的,就是我有4个的时候判别直接缩成2个肯定是false,因此我们不能一次缩两个,我们可以左边或者右边缩,如下表达式
//dp[i][j]=(j-i+1>=3)&&(dp[i+1][j]&&arr[i]<arr[i+1])||(dp[i][j-1]&&arr[j]<arr[j-1]);
//可以看出,我们需要使用左下角的值,因此我们必须确保我们需要的左下角的值能求出来
//那么我们就可以从下往上,从左往右
//当然我们必须确保可以为true的条件哦,也就是在临街的长度为3的时候
for(int i=n-1;i>=0;i--){
for(int j=i+1;j<n;j++){
if(j-i+1==3){
if(arr[i]<arr[i+1]&&arr[i+1]>arr[i+2])dp[i][j]=true;
}
else{
dp[i][j]=(j-i+1>=3)&&(dp[i+1][j]&&arr[i]<arr[i+1])||(dp[i][j-1]&&arr[j]<arr[j-1]);
}
if(dp[i][j]){
res=Math.max(res,j-i+1);
}
}
}
return res;*/
}
19.重建二叉树【前序和中序】
https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/ 【剑指offer的题】
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 返回如下的二叉树:
3
/ \ 9 20 / \ 15 7
public TreeNode buildTree(int[] preorder, int[] inorder) {
TreeNode res=dfs(preorder,0,inorder,0,inorder.length-1);
return res;
}
private TreeNode dfs(int[] preorder,int psIndex, int[] inorder,int isIndex,int ieIndex){
if(isIndex>ieIndex){
return null;
}
TreeNode res=new TreeNode(preorder[psIndex]);
int iMid=isIndex;
for(int i=isIndex;i<=ieIndex;i++){
if(inorder[i]==preorder[psIndex]){
iMid=i;
break;
}
}
res.left=dfs(preorder,psIndex+1,inorder,isIndex,iMid-1);
res.right=dfs(preorder,psIndex+iMid-isIndex+1,inorder,iMid+1,ieIndex);
return res;
}
中序和后序
public TreeNode buildTree(int[] inorder, int[] sufixorder) {
int len=inorder.length;
return buildTree(inorder,0,len-1,sufixorder,0,len-1);
}
private TreeNode buildTree(int[] inorder,int is,int ie, int[] sufixorder,int ss,int se){
if(ss>se)return null;
int val=sufixorder[se];
TreeNode treeNode=new TreeNode(val);
int mid=0;
for(int i=is;i<=ie;i++){
if(inorder[i]==val){
mid=i;
break;
}
}
treeNode.left=buildTree(inorder,is,mid-1,sufixorder,ss,ss+mid-is-1);
treeNode.right=buildTree(inorder,mid+1,ie,sufixorder,ss+mid-is,se-1);
return treeNode;
}
20.LC671. 二叉树中第二小的节点
难度简单104收藏分享切换为英文关注反馈
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为
2或0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1:
输入:
2
/ \
2 5
/ \
5 7
输出: 5
说明: 最小的值是 2 ,第二小的值是 5 。示例 2:
输入:
2
/ \
2 2
输出: -1
说明: 最小的值是 2, 但是不存在第二小的值。public int findSecondMinimumValue(TreeNode root) {
//根节点一定是最小值
if(root==null||root.left==null)return -1;//因为题目要求出现只能2个,因此右边可以不判别
return dfs(root,root.val);
}
private int dfs(TreeNode root,int min){
if(root==null) return -1;
if(root.val>min)return root.val;//由题意知,任何一个树的根节点的值一定是最小的
//找不到就是-1,也就是必须要比min大的
int left=dfs(root.left,min);
int right=dfs(root.right,min);
if(left==-1)return right;
if(right==-1)return left;
return Math.min(left,right);
}
21.LC873. 最长的斐波那契子序列的长度
如果序列
X_1, X_2, ..., X_n满足下列条件,就说它是 斐波那契式 的:
n >= 3对于所有
i + 2 <= n,都有X_i + X_{i+1} = X_{i+2}给定一个严格递增的正整数数组形成序列,找到
A中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。(回想一下,子序列是从原序列
A中派生出来的,它从A中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如,[3, 5, 8]是[3, 4, 5, 6, 7, 8]的一个子序列)示例 1:
输入: [1,2,3,4,5,6,7,8]
输出: 5
解释:
最长的斐波那契式子序列为:[1,2,3,5,8] 。示例 2:
输入: [1,3,7,11,12,14,18]
输出: 3
解释:
最长的斐波那契式子序列有:
[1,11,12],[3,11,14] 以及 [7,11,18] 。
public int lenLongestFibSubseq(int[] A){
HashMap<Integer,Integer> hashIndex=new HashMap<>();
int len=A.length;
for (int i = 0; i < len; i++) {
hashIndex.put(A[i],i);
}
int res=0;
//dp[i][j]代表结尾到i j一共有几个满足条件的(也就是说考虑结尾是i j的斐波那契数列有几个)
int[][] dp=new int[len][len];
for(int k=0;k<len;k++){
for(int j=0;j<k;j++){
int index=hashIndex.getOrDefault(A[k]-A[j],-1);
if(index>=0&&index<j){
dp[j][k]=dp[index][j]==0?3:dp[index][j]+1;
res=Math.max(res,dp[j][k]);
}
}
}
return res;
}
22.删除重复连续的数字 如1221 输出为空
个人思路:我先放进去,然后判别是否和我最后插入进来的重复,如果是的话,则这些后面重复的我直接跳过,跳过完后,我需要将这个也移除。
public String getNewStr(String str){
Deque<Character> queue=new LinkedList<>();
int len=str.length();
char c;
for(int i=0;i<len;i++){
c=str.charAt(i);
if(queue.isEmpty()){
queue.add(c);
}
else{
if(queue.getLast()==c){
//这些重复的都不添加进去
while (i<len&&queue.getLast()==str.charAt(i)){
i++;
}
queue.removeLast();
i--;//因为i下次循环还要++,因此我这里应该定位到前一个,这样循环到这一位才是对的
}
else{
queue.add(c);
}
}
}
return queue.toString();
}
23.LC538把二叉搜索树转换为累加树
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输入: 原始二叉搜索树: 5 / \ 2 13
输出: 转换为累加树: 18 / \ 20 13
class Solution {
//1ms
int sum=0;
public TreeNode convertBST(TreeNode root) {
if (root != null) {
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
}
return root;
}
//3ms
//就是二叉树中序遍历反过来,中序是左 上 右 反过来呗 我就 右 上 左 (因为大的都在右边)
/*public TreeNode convertBST(TreeNode root) {
//这是AVL,也就是右节点的左<上<右
//利用这个规律开始计算(最右节点肯定最大,因此它需要+0,其余的都不行,因此我们直接中序遍历给反过来,就好了)
//变成->右,上,左
//先加完,再给他赋值
Stack<TreeNode> stack=new Stack<>();
if(root!=null){
stack.push(root);
}
int sum=0;
int tempSum;
TreeNode curNode=root;
while(!stack.isEmpty()){
if(curNode!=null&&curNode.right!=null){
stack.push(curNode.right);
curNode=curNode.right;
}
else{
curNode=stack.pop();
tempSum=sum;
sum+=curNode.val;
curNode.val+=tempSum;
if(curNode!=null&&curNode.left!=null){
stack.push(curNode.left);
curNode=curNode.left;
}
else{
curNode=null;
}
}
}
return root;
}*/
//11ms
//先取出所有节点的值,排序(这个解法针对于任意树(当前写法是节点值没有重复的,重复就不对了,hash哪里需要改的),本题是AVL)
/*if(root==null||(root.left==null&&root.right==null))return root;
List<Integer> list=new ArrayList<>();
Queue<TreeNode> queue=new LinkedList<>();
if(root!=null)
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
while(size-->0){
TreeNode temp=queue.poll();
list.add(temp.val);
if(temp.left!=null){
queue.add(temp.left);
}
if(temp.right!=null){
queue.add(temp.right);
}
}
}
Collections.sort(list,(o1,o2)->(o2-o1));
HashMap<Integer,Integer> hashMap=new HashMap<>();
int sum=0;
hashMap.put(list.get(0),0);
//这里是严格的AVL不含重复的节点值
for(int i=1;i<list.size();i++){
hashMap.put(list.get(i),hashMap.get(list.get(i-1))+list.get(i-1));
}
if(root!=null)
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
while(size-->0){
TreeNode temp=queue.poll();
temp.val+=hashMap.get(temp.val);
if(temp.left!=null){
queue.add(temp.left);
}
if(temp.right!=null){
queue.add(temp.right);
}
}
}
return root;*/
}
24.LC739每日温度
请根据每日 气温 列表,重新生成一个列表。对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
思路:我们当然可以从当前点出发,暴力解决,但是显然时间复杂度过高
我们可以使用栈来解决,也就是将当前节点索引和值压入栈,下一个来的时候,我判断当前顶端是不是比我这个值小,如果是的话,则将顶端弹出,并且更新它的天数,继续做知道找不到或者栈为空,则将这个元素压入,个人实现代码如下:
public int[] dailyTemperatures(int[] arr) {
int len=arr.length;
int[] res=new int[len];
Stack<MyPoint> stack=new Stack<>();
MyPoint temp;
for(int i=0;i<len;i++){
if(stack.isEmpty()){
stack.push(new MyPoint(i,arr[i]));
}
else{
//temp=stack.peek();
while(!stack.isEmpty()&&stack.peek().val<arr[i]){
res[stack.peek().index]=i-stack.peek().index;
stack.pop();
}
stack.push(new MyPoint(i,arr[i]));
}
}
return res;
}
class MyPoint{
int index;
int val;
public MyPoint(int x,int y){
this.index=x;
this.val=y;
}
}
25.LC315. 计算右侧小于当前元素的个数
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质:
counts[i]的值是nums[i]右侧小于nums[i]的元素的数量。示例:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
思路:same as https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/ 我们使用归并排序来使用,本题我们需要比这个链接题做的要多一些,因为他需要确定每个索引位置对应后面比他小的个数,这样我们就没法用一个sum来全部统计,因此我们使用index数组,记录他其实index,随着他的位置变化,他的index也跟着他走,这样我就能一直知道它对应起始的index在哪,我创建一个ans数组,每次我按index位置找ans去+1,这样答案也就出来了
//可以再归并的时候,我们统计
int[] ans;
public List<Integer> countSmaller(int[] nums) {
int len=nums.length;
this.ans=new int[len];
int[] indexs=new int[len];
for(int i=0;i<len;i++){
indexs[i]=i;
}
mergeSort(nums,indexs,0,len-1,new int[len],new int[len]);
List<Integer> arrList=new ArrayList<>();
for(int i=0;i<len;i++){
arrList.add(ans[i]);
}
return arrList;
}
//indexs记录我们移动式nums各个数字变动所在的位置
private void mergeSort(int[] arr,int[] indexs,int leftIndex,int rightIndex,int[] temp,int[] tempIndex){
if(leftIndex>=rightIndex)return;
int mid= (leftIndex+rightIndex)/2;
mergeSort(arr,indexs,leftIndex,mid,temp,tempIndex);
mergeSort(arr,indexs,mid+1,rightIndex,temp,tempIndex);
int l=mid,r=rightIndex,t=rightIndex,ti=rightIndex;
while(l>=leftIndex&&r>mid){
if(arr[l]>arr[r]){
temp[t--]=arr[l];
tempIndex[ti--]=indexs[l];
ans[indexs[l]]+=r-mid;
l--;
}
else{
temp[t--]=arr[r];
tempIndex[ti--]=indexs[r];
r--;
}
}
while(l>=leftIndex){
temp[t--]=arr[l];
tempIndex[ti--]=