HDU1348--Wall(凸包）

佷裸的一道凸包题，就是多组数据，每组给你点数和圆的半径，然后一堆坐标，最后输出圆的周长加上这个最小凸包的周长。

这里我用的是Graham_scan方法，具体的就是：

1.我们取Y坐标最小的点A作为原点建立平面直角坐标系，然后以剩余点与X轴的夹角从小到大逆时针依次标记，可以不难发现A,B必在这个最小凸包上

 

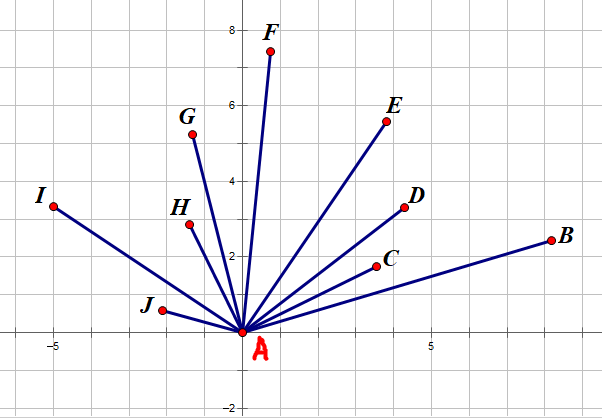
2.然后按照字母顺序连接，首先连接AB，然后是BC，我们发现∠ABC是小于180°的，所以我们暂且认为C是在这个最小凸包上的

 

3.现在，我们继续连接CD，但此时GG的事就是我们发现∠BCD为大约180°的角如果我们认为D也是凸包上的点，这里就会出现一个凹陷，因此我们既要保证C、D都在凸包内，又要不出现凹陷，只能去掉BC而选BD

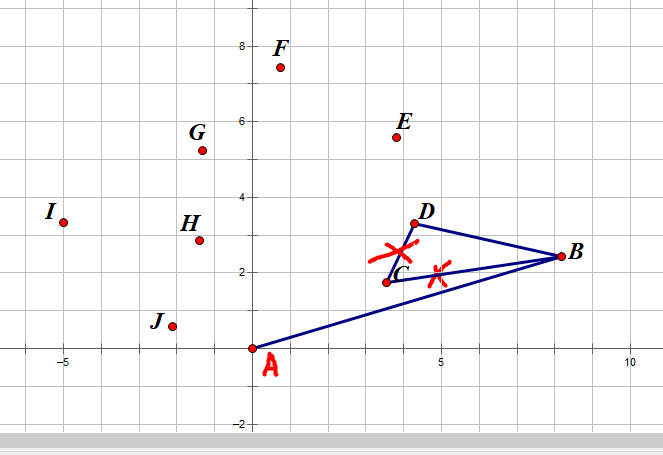
4.以此类推，不难发现我们的最小凸包应该长这个样子

 

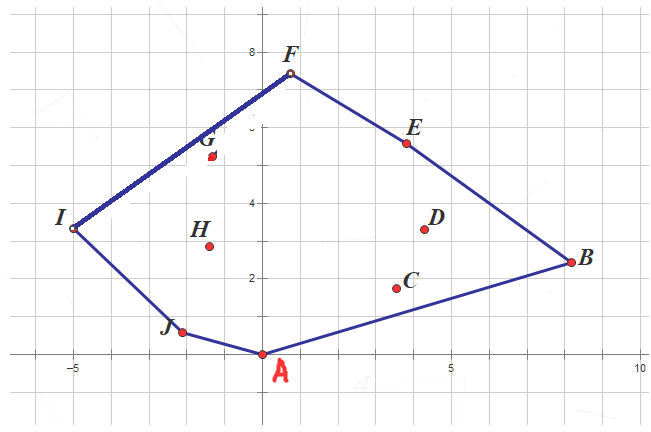
5.最后，用两点距离公式来求出周长即可

Q：如何判断夹角是否为凸凹？

我们用叉乘来判断

 

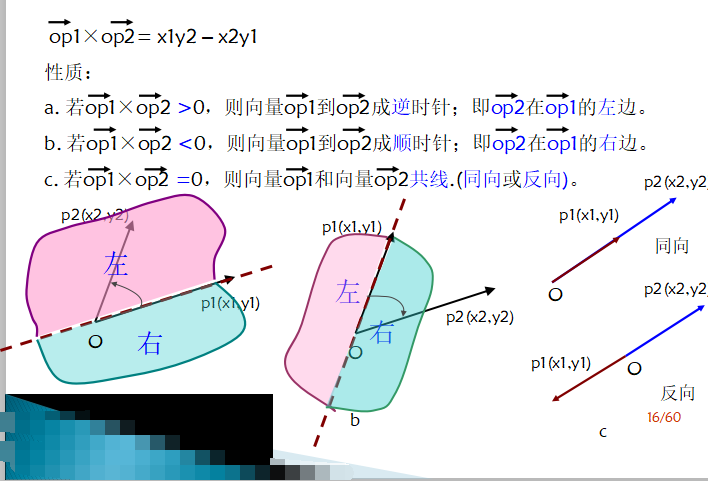
 这里的左边即为小于180°，右边为大于180°（可以画图证明）

这样就可以判断了。

丑陋的代码（这道题别忘加上2πr）：

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int  maxn=1010;
const double Pi=acos(-1.0);
struct Node
{
    double x,y;
}p[maxn],P[maxn];
int n,tot;
double ans,l;
double X(Node A,Node B,Node C)
{
    return (B.x-A.x)*(C.y-A.y)-(C.x-A.x)*(B.y-A.y);
    
}//叉乘 
double len(Node A ,Node B)
{
    return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
}//距离 
bool cmp(Node A,Node B)
{
    double pp=X(p[0],A,B);
    if(pp>0) return true;
    if(pp<0) return false;
    return len(p[0],A)<len(p[0],B); 
}//按夹角逆时针排序 
int main()
{
    int t;
    scanf("%d",&t);
    for(int u=1;u<=t;u++)
    {
        if(u!=1)printf("\n");
        scanf("%d%lf",&n,&l);
        ans=2*Pi*l;
        for(int i=0;i<n;i++)
        scanf("%lf%lf",&p[i].x,&p[i].y);
        if(n==1)
        {
            printf("%.0f\n",ans);
        }
        else if(n==2)
        {
            printf("%.0f\n",ans+len(p[0],p[1]));

        }
        else 
        {
            for(int i=0;i<n;i++)
            {
                if(p[i].y<p[0].y)
                {
                    swap(p[i],p[0]);
                }
                else if(p[i].y==p[0].y&&p[i].x<p[0].x)
                {
                    swap(p[i],p[0]);
                }
            }
            sort(p+1,p+n,cmp);
            P[0]=p[0];
            P[1]=p[1];
            tot=1;
            for(int i=2;i<n;i++)
            {
                while(tot>0&&X(P[tot-1],P[tot],p[i])<=0)
                tot--;
                tot++;
                P[tot]=p[i];
            }
            for(int i=0;i<tot;i++)
            ans+=len(P[i],P[i+1]);
            ans+=len(P[0],P[tot]);
            printf("%.0f\n",ans); 
        }
    }
    return 0;
} 

感觉说的应该是不太好，有什么错误请指出，谢谢