leetcode 每日一题 96. 不同的二叉搜索树

动态规划
思路:
用G(n)来表示长度为n的序列的不同二叉搜索树个数,当n=0时,只能构成空树这一种情况,即G(0)=1;当n=1时,只能构成一个只有根节点的树这一种情况,即G(1)=1。
给定序列1.....n,可以选出数字 i 作为根,1.....(i-1)序列为其左子树,(i+1)....n序列为其右子树,对左右子树进行同样根节点遍历,可以递归的构造左右子树。若以 i 为根的左子树构造情况有m种,右子树构造情况有n种,则以i为根的构造情况总数为m*n种。
则G(n)为1....n序列中,以每个根节点构造出的所有子树之和。而在1......(i-1)左子树序列中,所能构造的子树个数跟子树节点的值是没有关系的,可以直接通过G(i-1)获得,同理右子树序列的可能数为G(n-i),则
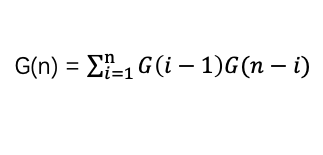
代码:
class Solution: def numTrees(self, n: int) -> int: G = [0]*(n+1) G[0], G[1] = 1, 1 for i in range(2, n+1): for j in range(1, i+1): G[i] += G[j-1] * G[i-j] return G[n]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号