leetcode 每日一题 37. 解数独

回溯法

思路:

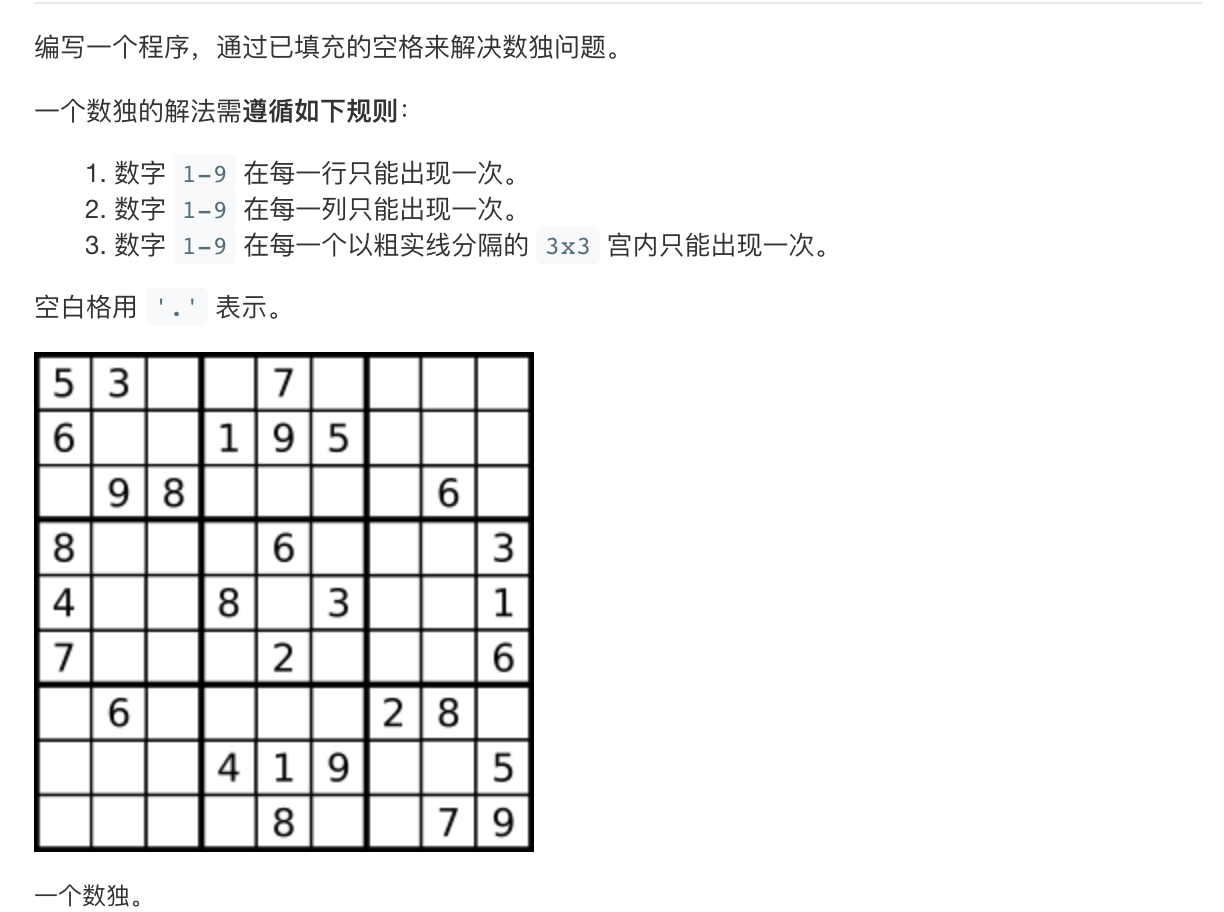
①首先建立三个数组，分别记录每行每列和每个3x3宫内出现过的数字，从第0行第0列开始进行②

②如果遇到的字符不是' . '，则进行填入下一个值操作。如果遇到字符是' . '则填数字，可以填入数字范围为1-9，每填入一个数字需要进行判断，如果这个数字在对应所在行、列、和3x3宫内出现过，则此数字不能填入。如果没有出现过，则填入数字，同时更新三个数组和board中相应位置的值。接着填入下一个值，如果在进行填入下一个值这步操作后，问题没有的到解决，意味着填入的数字无法得到最终解，则还原board填入的值，同时更新三个数组中相应位置值，继续尝试下一个可能的数字。

③填入下一个数所要做的操作是，如果当前数字已经是最后一个数字，则问题解决，得到答案，如果不是最后一个数字，根据判断列号得到下一个要填入数字的下标，回溯到②

如下图:

代码:

from collections import defaultdict
class Solution:
    def solveSudoku(self, board):
        def could_place(d, row, col):
            return not (d in rows[row] or d in columns[col] or \
                    d in boxes[box_index(row, col)])
        def place_number(d, row, col):
            rows[row][d] += 1
            columns[col][d] += 1
            boxes[box_index(row, col)][d] += 1
            board[row][col] = str(d)   
        def remove_number(d, row, col):
            del rows[row][d]
            del columns[col][d]
            del boxes[box_index(row, col)][d]
            board[row][col] = '.'     
        def place_next_numbers(row, col):
            if col == N - 1 and row == N - 1:
                nonlocal sudoku_solved
                sudoku_solved = True   
            else:
                if col == N - 1:
                    backtrack(row + 1, 0)
                else:
                    backtrack(row, col + 1)     
        def backtrack(row = 0, col = 0):
            if board[row][col] == '.':
                for d in range(1, 10):
                    if could_place(d, row, col):
                        place_number(d, row, col)
                        place_next_numbers(row, col)
                        if not sudoku_solved:
                            remove_number(d, row, col)
            else:
                place_next_numbers(row, col)  
        n = 3
        N = n * n
        box_index = lambda row, col: (row // n ) * n + col // n
        rows = [defaultdict(int) for i in range(N)]
        columns = [defaultdict(int) for i in range(N)]
        boxes = [defaultdict(int) for i in range(N)]
        for i in range(N):
            for j in range(N):
                if board[i][j] != '.': 
                    d = int(board[i][j])
                    place_number(d, i, j)
        sudoku_solved = False
        backtrack()