数据结构---链表及约瑟夫环问题带来的思考
链表和数组一样也是线性表的一种。和数组不同,它不需要再内存中开辟连续的空间。
链表通过指针将一组零散的内存块连接在一起。我们把内存块称为链表的“结点”(是节点还是结点,结点连接起来打个结所以叫“结点”?开个玩笑),也就是说这些结点可以在内存的任意地方,只要有其他的结点的指针指向这个位置就可以。
链表又分为单向链表,双向链表,循环链表
单向链表
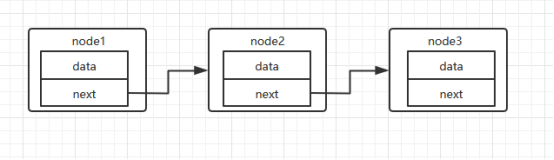
循环链表:最后一个节点指向第一个结点

双向链表:比单向链表多了一个前驱指针,指向前面一个结点

从上面的结构和内存中的储存结构来看,就可以发现链表相比数组来说,随机查询效率是O(n),只有从头结点开始查找;但是它的插入修改效率比数组高,找到位置之后只需要修改下指针指向,而不需要进行后续元素的迁移。理论上来说是无限容量,不像数组满了还需要扩容,扩容还要重新申请内存,然后迁移数据,链表只需要在内存找个一小块空地,放好数据,让前面那个指向这里就是了。
我们也可以看到双向链表比单向链表更灵活,因为通过一个结点可以找到前后两个结点。但是多了个指针所占空间肯定比单向链表大。
Java中LinkedList就是一个双向链表。
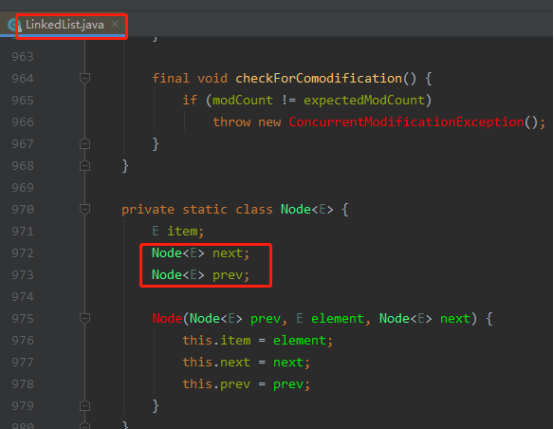
简单实现一个单向链表
package com.nijunyang.algorithm.link; /** * Description: * Created by nijunyang on 2020/3/31 22:09 */ public class MyLinkedList<E> { private Node<E> head; private int size = 0; /** * 头部插入O(1) * @param data */ public void insertHead(E data){ Node newNode = new Node(data); newNode.next = head; head = newNode; size++; } public void insert(E data,int position){ if(position == 0) { insertHead(data); }else{ Node cur = head; for(int i = 1; i < position ; i++){ cur = cur.next; //一直往后遍历 } Node newNode = new Node(data); // newNode.next = cur.next; //新加的点指向后面 保证不断链 cur.next = newNode; //把当前的点指向新加的点 size++; } } public void deleteHead(){ head = head.next; size--; } public void delete(int position){ if(position == 0) { deleteHead(); }else{ Node cur = head; for(int i = 1; i < position ; i ++){ cur = cur.next; //找到删除位置的前一个结点 } cur.next = cur.next.next; //cur.next 表示的是删除的点,后一个next就是我们要指向的 size--; } } public int size( ){ return size; } public String toString( ){ if (size == 0) { return "[]"; } StringBuilder sb = new StringBuilder(); sb.append('['); Node<E> node = head; sb.append(node.value); int counter = 0; for (;;) { if (++counter == size) { break; } sb.append(","); node = node.next; sb.append(node.value); } sb.append(']'); return sb.toString(); } public static void main(String[] args) { MyLinkedList myList = new MyLinkedList(); myList.insertHead(5); System.out.println(myList); myList.insertHead(7); System.out.println(myList); myList.insertHead(10); System.out.println(myList); myList.delete(0); System.out.println(myList); myList.deleteHead(); System.out.println(myList); myList.insert(11, 1); System.out.println(myList); } private static class Node<E>{ E value; //值 Node<E> next; //下一个的指针 public Node() { } public Node(E value) { this.value = value; } } }
约瑟夫环问题:
说到链表就要提一个下约瑟夫环问题:N个人围成一圈,第一个人从1开始报数,报M的被杀掉,下一个人接着从1开始报,循环反复,直到剩下最后一个。看到这个就想到用循环链表来实现,无限remove知道链表只剩下一个为止。
之前去力扣上面做的时候就用循环链表实现了下,验证是可以过的,但是代码提交之后显示超时,过不了。仔细分析之后之后发现循环链表实现,时间线复杂度是O(n*m),如果数据大了,必定是个问题。然后就换了,数组(ArrayList)来实现,每次移除之后大小减一,通过取模size来实现循环报数的效果。会发现数组实现的,时间复杂度仅仅是O(n),两种方式代码如下:
package com.nijunyang.algorithm.link; import java.util.ArrayList; /** * Description: * Created by nijunyang on 2020/3/30 21:49 */ public class Test { public static void main(String[] args){ long start = System.currentTimeMillis(); int result = yuesefuhuan_link(70866, 116922); long end = System.currentTimeMillis(); System.out.println(result); System.out.println("链表耗时:" + (end - start)); System.out.println("-------------------------"); start = System.currentTimeMillis(); result = yuesefuhuan_arr(70866, 116922); end = System.currentTimeMillis(); System.out.println(result); System.out.println("数组耗时:" + (end - start)); } /** * 数组约瑟夫环 */ public static int yuesefuhuan_arr(int n, int m) { int size = n; ArrayList<Integer> list = new ArrayList<>(size); for (int i = 0; i < size; i++) { list.add(i); } int index = 0; while (size > 1) { //取模可以回到起点 index = (index + m - 1) % size; list.remove(index); size--; } return list.get(0); } /** * 循环链表约瑟夫环力扣超时 * @param n * @param m * @return */ public static int yuesefuhuan_link(int n, int m) { if (n == 1) { return n - 1; } Node<Integer> headNode = new Node<>(0); Node<Integer> currentNode = headNode; //尾结点 Node<Integer> tailNode = headNode; for (int i = 1; i < n; i++) { Node<Integer> next = new Node<>(i); currentNode.next = next; currentNode = next; tailNode = currentNode; } //成环 tailNode.next = headNode; //保证第一次进去的时候指向头结点 Node<Integer> remove = tailNode; Node<Integer> preNode = tailNode; int counter = n; while (true) { for (int i = 0; i < m; i++) { //一直移除头结点则,前置结点不动 if (m != 1) { preNode = remove; } remove = remove.next; } preNode.next = remove.next; if (--counter == 1) { return preNode.value; } } } static class Node<E>{ E value; Node next; public Node() { } public Node(E value) { this.value = value; } } }
运行之后看下结果对比,我的机器CPU还算可以I7-8700,内存16G,结果都是一样的说明我们的两种算法都是正确的,但是耗时的差别就很大很大了
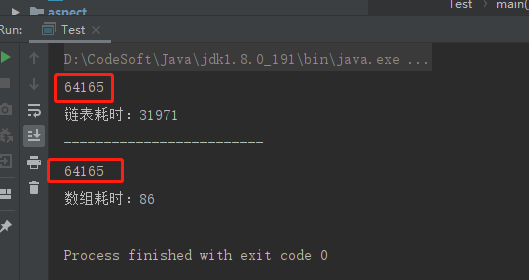
链表耗时30多秒,数组耗时86毫秒,,差不多400倍的差距。
之前也说到数据在内存中是连续的,可以借助CPU的缓存机制预读数据,而链表每次还需要根据指针去寻找。其次就是两种方式时间复杂度是不一样的,我们上面的用的数据70866, 116922。O(n*m)和O(n)差距有多大。所以说不同算法对程序的性能影响还是很大的,这应该就是体现了“算法之美”了吧。提到这个问题,最先想到的可能就是循环链表来解决,最后却发现,循环链表并不是一个很好的解决方式。这就像我们平时写代码,需求下来的时候想着怎样怎样去实现,但是最后上线版本中,肯定改了又改的版本,有些方案可能整体换血都可能。再者就是从这个问题中就看出了算法的重要性。当然在力扣上面还有一种反推法实现的,比数组实现的代码更少,性能更高,感兴趣的自己搜,这里就不列出来对比了。





