numpy深度学习案例

1、定义模型及参数

1、假设有如下一层隐藏层的神经网络,使用relu函数作为激活函数
\(y = w2 * h(w1*x + b1) +b2\)





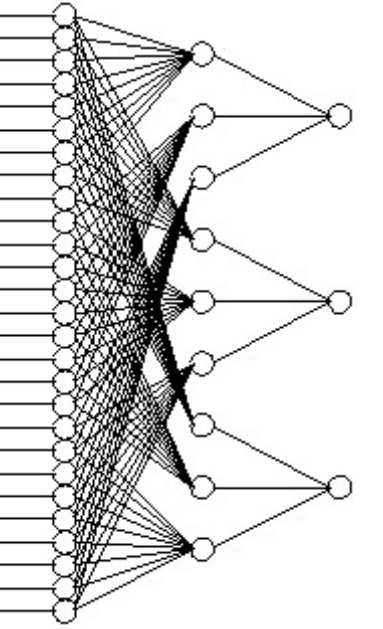
2、假设输入是27维向量， 输出是3维向量，设计有一个隐藏层纬度是9，训练数据量是100，学习率是10^-4

n, x_len, y_len, h_len = 100, 27, 3, 9
learn_rate = 1e-4

2、生成参数

这里随机生成x和y， 假设其中有一定的线性关系，初始化w1,w2,b1,b2

x = np.random.randn(n, x_len)
y = x.dot(np.random.randn(x_len,y_len))
w1 = np.random.randn(x_len, h_len)
b1 = np.random.randn(n, h_len)
w2 = np.random.randn(h_len, y_len)
b2 = np.random.randn(n, y_len)

3、计算得分

# 前向传播，计算出predicate
h1 = np.matmul(x, w1) + b1
h1_activated = np.maximum(0, h1)  # 使用 RELU 激活函数
predicate = np.matmul(h1_activated, w2) + b2

4、定义损失函数

这里使用平方损失函数

loss = np.square(predicate - y).sum()

5、方向传播

反向传播，要计算出需要学习的参数的梯度, 这里满足求导链式法则，要注意矩阵转置。

# loss = (w2 * h(w1*x + b1) +b2 - y) ^ 2
d_loss_predicate = 2.0 * (predicate - y)  # (n, y)
d_loss_b2 = d_loss_predicate  # (n, y)
d_loss_w2 = h1_activated.T.dot(d_loss_predicate)  # (h, y)
d_loss_relu = d_loss_predicate.dot(w2.T)  # (n, h)
d_loss_relu[h1 < 0] = 0  # (n, h)
d_loss_b1 = d_loss_relu  # (n, h)
d_loss_w1 = x.T.dot(d_loss_relu)  # (x, h)

6、更新参数

w1 -= learn_rate * d_loss_w1
w2 -= learn_rate * d_loss_w2
b1 -= learn_rate * d_loss_b1
b2 -= learn_rate * d_loss_b2

7、完整代码

import numpy as np

n, x_len, y_len, h_len = 100, 27, 3, 9
learn_rate = 1e-4

x = np.random.randn(n, x_len)
y = x.dot(np.random.randn(x_len,y_len))

w1 = np.random.randn(x_len, h_len)
b1 = np.random.randn(n, h_len)
w2 = np.random.randn(h_len, y_len)
b2 = np.random.randn(n, y_len)


for step in range(2000):
    # 前向传播，计算出predicate
    h1 = np.matmul(x, w1) + b1
    h1_activated = np.maximum(0, h1)  # 使用 RELU 激活函数
    predicate = np.matmul(h1_activated, w2) + b2

    # 定义损失函数
    loss = np.square(predicate - y).sum()

    # 反向传播，计算梯度
    # loss = (w2 * h(w1*x + b1) +b2 - y) ^ 2
    d_loss_predicate = 2.0 * (predicate - y)  # (n, y)
    d_loss_b2 = d_loss_predicate  # (n, y)
    d_loss_w2 = h1_activated.T.dot(d_loss_predicate)  # (h, y)
    d_loss_relu = d_loss_predicate.dot(w2.T)  # (n, h)
    d_loss_relu[h1 < 0] = 0  # (n, h)
    d_loss_b1 = d_loss_relu  # (n, h)
    d_loss_w1 = x.T.dot(d_loss_relu)  # (x, h)

    # 跟新参数
    w1 -= learn_rate * d_loss_w1
    w2 -= learn_rate * d_loss_w2
    b1 -= learn_rate * d_loss_b1
    b2 -= learn_rate * d_loss_b2

    print("step:",step,"loss:", loss)

可以看到效果如下

step: 0 loss: 41360.61046579813
step: 1 loss: 16972.5436623805
step: 2 loss: 13102.822129263155
step: 3 loss: 11106.865601323854
step: 4 loss: 9925.898376533689
step: 5 loss: 9147.34649665557
step: 6 loss: 8577.78981529676
step: 7 loss: 8130.194652344302
step: 8 loss: 7759.544954438901
step: 9 loss: 7431.012977041601
step: 10 loss: 7131.920034469347
step: 11 loss: 6853.743130090565
step: 12 loss: 6590.067965291491
......
......
step: 1990 loss: 87.70062357538693
step: 1991 loss: 87.62600812969745
step: 1992 loss: 87.55114755604917
step: 1993 loss: 87.47891216042798
step: 1994 loss: 87.40599235015554
step: 1995 loss: 87.33357855182985
step: 1996 loss: 87.25899848192097
step: 1997 loss: 87.18514488655194
step: 1998 loss: 87.11068127826968
step: 1999 loss: 87.0386653373821