计算几何基础知识
计算几何基础知识
向量,极坐标
基础概念高中课本应该讲了吧 贴下 oiwiki 链接:向量,极坐标
平面向量在计算几何中一般用坐标来描述, 表示的是起点在 ,而终点在 的平面向量。
所以我们也可以用点来描述向量。
理解下文的式子最好都将向量看成起点在 ,终点在 的一个”箭头“。
基本运算:
设 , 。
那么有:
。
。
所以点的加减法可以理解成其表示向量的加减法。
而加减法的结果都是向量。
如果 的夹角为 。那么有:
。
我们称其为 的点积。
以上我们的向量的运算都是在二维平面意义下的。
而在三维空间中我们有空间向量。也就是三维空间下的向量,类似平面向量,我们同样可以用一个点的坐标来描述空间向量。
设 。而上述二维平面下的运算,我们可以看成是空间向量 在 值相等时的运算。
定义向量 的向量积为 。其结果是一个向量。
这个玩意儿在平面上的应用就是用来判断两个向量的关系位置。
因为 。
设 之间的夹角为 ,且他们的 均为 。
那么 。
易知向量积的方向由 决定。又根据右手定则(用来看向量积方向的),我们可以得出结论:
如果
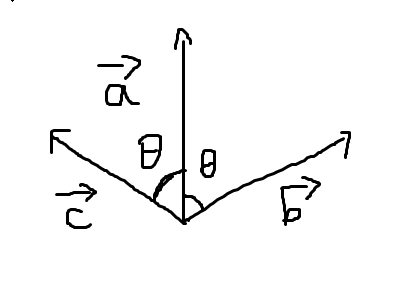
那么 就由 在 平面内逆时针旋转 度得到。
反之, 就由 在 平面内顺时针旋转 度得到。
时他俩重合奥。
就像这样
极角排序
建立极坐标系,以 为极点, 为极轴 ,正方向定义为逆时针方向。
设 为一个点 (看做一个向量也行),那么这个点的极角是 。
一种做法是直接利用 函数求出极角进行排序,不过运算结果是 double,只能说懂得都懂。
还有一种做法就是先求出极角终边在哪个象限,然后利用叉乘求解。
划成四个象限似乎有些麻烦。
因为叉乘的应用范围是 。所以我们只要将一个平面划为两部分。如果两个点落在同一部分,那么利用叉乘求解,落在不同部分我们就根据自己定义来直接判断即可。
举个例子,如果我们要让 第四象限的角 第一象限的角 第二 第三。
那么我们将 划为第一部分,( 代表 半轴, 就是负半轴),另一块是第二部分,如果两个点落在第一部分,那么用叉乘计算,如果 ,那么 的极角小于 的极角。
如果落在不同部分,根据我们的定义,第一部分的就小于第二部分。
凸包
这一块 oiwiki 讲的很详细了,我偷个懒。凸包。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】