「USACO21DEC」Paired Up P
「USACO21DEC」Paired Up P
首先现将荷斯坦牛和更赛牛分开并且按位置从小到大排序。
考虑 T=1 的子任务。
容易想到 \(f_{i,j}\) 表示前 \(i\) 头荷斯坦牛和前 \(j\) 头更赛牛匹配后能得到的配对奶牛的最大重量和。
不难发现答案就是 \(\sum_{i=1}^{n}Y_i-f_{cnt1,cnt2}\),其中 \(cnt1\) 表示荷斯坦牛的个数,\(cnt2\) 表示更赛牛的个数。
定义 check(i,j) 函数表示判断第 \(i\) 头荷斯坦牛和更赛牛能不能匹配。
转移代码如下:
for(int i=1;i<=cnt1;++i)
{
for(int j=1;j<=cnt2;++j)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(check(i,j)) f[i][j]=max(f[i][j],f[i-1][j-1]+A[i].y+B[j].y);
}
}
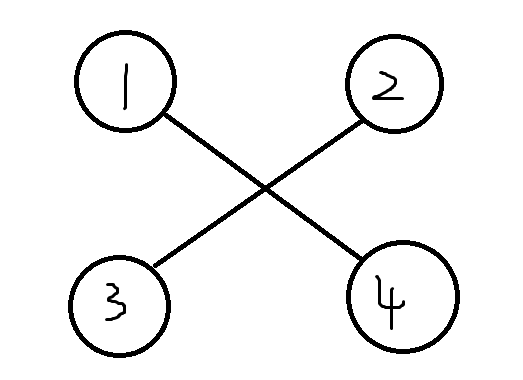
这么转移我们会发现一个问题。可能最优解是这么匹配的。
即 \(1,4\) 匹配,\(2,3\) 匹配。
这种情况我们这么转移是转移不到的,但是容易发现,既然 \(2,3\) 能匹配且 \(1,4\) 能匹配,那么 \(2,4\) 一定能匹配,而同理 \(1,3\) 也一定能匹配。
所以我们 dp 中会转移出 \(1,3\) 匹配 \(2,4\) 匹配的状况,而这两种情况是等效的。
所以我们的转移式是正确的。
考虑 T= 2 的子任务
由于配对是极大的,所以我们要让一只奶牛计入答案的贡献时,必须要让这只奶牛的配对范围内没有能与它配对的奶牛。
继续考虑 \(f_{i,j}\) 表示前 \(i\) 头荷斯坦牛和 \(j\) 头更赛牛所能形成未配对的奶牛的最大重量和。
注意到这个状态并不能告诉我们能不能使一个奶牛计入未配对的贡献,所以多开一维。
用 \(f_{i,j,0/1}\) 表示 前 \(i\) 头荷斯坦牛和 \(j\) 头更赛牛已经处理完毕且下一只荷斯坦牛/更赛牛可以计入贡献。
那么有
那 \(f_{i,j,0}\) 与 \(f_{i,j,1}\) 间如何转移?
\(f_{i,j,0}\) 表示下只能转移荷斯坦牛,说明第 \(i\) 只荷斯坦牛可能是未匹配的,所以我们要找到第一只不能和第 \(i\) 只荷斯坦牛配对的更赛牛的前一个位置 \(j+len\),如果 \(i+1\) 到 \(i+len\) 与 \(j+1\) 到 \(j+len\) 都能匹配上,那么 \(f_{i,j,0}\) 就能转移到\(f_{i+len,j+len,1}\)。
同理 \(f_{i,j,1}\) 也可以在对应条件下转移到 \(f_{i+len,j+len,0}\)。
那如果 \(f_{i,j,0}\) 的第 \(i\) 只荷斯坦牛是匹配过的,那上述转移就会出错,但是实际上这种情况的最优解会以 \(f_{i,j,0/1}\rightarrow f_{i,j,0/1}\) 这条式子转移上来。
代码如下:
memset(dp,-0x3f,sizeof dp);
dp[0][0][0]=dp[0][0][1]=0;
for(int i=cnt1;i>=1;--i)
{
for(int j=cnt2;j>=1;--j)
{
if(check(i,j)) match[i][j]=match[i+1][j+1]+1;
else match[i][j]=0;
}
}
for(int i=1,j=1;i<=cnt1;++i)
{
while(j<=cnt2&&(check(i,j)||B[j].x<A[i].x)) ++j;
nxtH[i]=j;
}
for(int i=1,j=1;i<=cnt2;++i)
{
while(j<=cnt1&&(check(j,i)||A[j].x<B[i].x)) ++j;
nxtG[i]=j;
}
nxtH[0]=nxtG[0]=1;
for(int i=0;i<=cnt1;++i)
{
for(int j=0;j<=cnt2;++j)
{
int step=max(nxtH[i]-j-1,0);
if(i+step<=cnt1&&match[i+1][j+1]>=step)
dp[i+step][j+step][1]=max(dp[i+step][j+step][1],dp[i][j][0]);
step=max(nxtG[j]-i-1,0);
if(j+step<=cnt2&&match[i+1][j+1]>=step)
dp[i+step][j+step][0]=max(dp[i+step][j+step][0],dp[i][j][1]);
if(i<cnt1&&j<cnt2&&check(i+1,j+1))
{
dp[i+1][j+1][0]=max(dp[i+1][j+1][0],dp[i][j][0]);
dp[i+1][j+1][1]=max(dp[i+1][j+1][1],dp[i][j][1]);
}
if(i<cnt1) dp[i+1][j][0]=max(dp[i+1][j][0],dp[i][j][0]+A[i+1].y);
if(j<cnt2) dp[i][j+1][1]=max(dp[i][j+1][1],dp[i][j][1]+B[j+1].y);
}
}
全部代码如下:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5e3+5;
int T,n,K,cnt1,cnt2;
char ty[MAXN][4];
int f[MAXN][MAXN],X[MAXN],Y[MAXN],dp[MAXN][MAXN][2];
int nxtH[MAXN],nxtG[MAXN],match[MAXN][MAXN];
struct COW
{
int x,y;
}A[MAXN],B[MAXN];
bool check(int i,int j)
{
if(abs(A[i].x-B[j].x)<=K) return true;
return false;
}
int main()
{
int testsum=0;
scanf("%d %d %d",&T,&n,&K);
for(int i=1;i<=n;++i)
scanf("%s %d %d",ty[i]+1,&X[i],&Y[i]),testsum+=Y[i];
for(int i=1;i<=n;++i)
{
if(ty[i][1]=='G') A[++cnt1]=COW{X[i],Y[i]};
else B[++cnt2]=COW{X[i],Y[i]};
}
if(T==1)
{
for(int i=1;i<=cnt1;++i)
{
for(int j=1;j<=cnt2;++j)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(check(i,j)) f[i][j]=max(f[i][j],f[i-1][j-1]+A[i].y+B[j].y);
}
}
int sum=-f[cnt1][cnt2];
for(int i=1;i<=n;++i) sum+=Y[i];
printf("%d\n",sum);
}
else
{
memset(dp,-0x3f,sizeof dp);
dp[0][0][0]=dp[0][0][1]=0;
for(int i=cnt1;i>=1;--i)
{
for(int j=cnt2;j>=1;--j)
{
if(check(i,j)) match[i][j]=match[i+1][j+1]+1;
else match[i][j]=0;
}
}
for(int i=1,j=1;i<=cnt1;++i)
{
while(j<=cnt2&&(check(i,j)||B[j].x<A[i].x)) ++j;
nxtH[i]=j;
}
for(int i=1,j=1;i<=cnt2;++i)
{
while(j<=cnt1&&(check(j,i)||A[j].x<B[i].x)) ++j;
nxtG[i]=j;
}
nxtH[0]=nxtG[0]=1;
for(int i=0;i<=cnt1;++i)
{
for(int j=0;j<=cnt2;++j)
{
int step=max(nxtH[i]-j-1,0);
if(i+step<=cnt1&&match[i+1][j+1]>=step)
dp[i+step][j+step][1]=max(dp[i+step][j+step][1],dp[i][j][0]);
step=max(nxtG[j]-i-1,0);
if(j+step<=cnt2&&match[i+1][j+1]>=step)
dp[i+step][j+step][0]=max(dp[i+step][j+step][0],dp[i][j][1]);
if(i<cnt1&&j<cnt2&&check(i+1,j+1))
{
dp[i+1][j+1][0]=max(dp[i+1][j+1][0],dp[i][j][0]);
dp[i+1][j+1][1]=max(dp[i+1][j+1][1],dp[i][j][1]);
}
if(i<cnt1) dp[i+1][j][0]=max(dp[i+1][j][0],dp[i][j][0]+A[i+1].y);
if(j<cnt2) dp[i][j+1][1]=max(dp[i][j+1][1],dp[i][j][1]+B[j+1].y);
}
}
printf("%d\n",max(dp[cnt1][cnt2][0],dp[cnt1][cnt2][1]));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号