COCI2016/2017 #1 D Mag 点分治

COCI2016/2017 #1 D Mag 点分治

​ 题目链接：COCI2016-2017#1

---

算法: 点分治

证明&结论：

​ 首先这题关于选出来的路径有一个结论：

• 路径上点权全为 \(1\)。
• 路径长度为 \(2\times l+1\)，有且只有一个权值为 \(2\) 的点在 \(l+1\) 这个位置，其他点权都为 \(1\)。
• 如果没有点权为 \(1\) 的点，那么答案就是最小的权值。

​ 首先声明一点，据题意可知，题目中出现的数据都是正整数，所以以下推导中出现的变量均为正整数。

​ 我们假设一个点权为 \(x\) 的点连接了两条魔力值分别为 \(\dfrac{a}{b},\dfrac{c}{d}\) 的路径。那么连接完后路径的魔力值就为 \(\dfrac{a\times c\times x}{b+d+1}\)。我们将这个魔力值与 \(\dfrac{a}{b}\) 相比，如果 \(\dfrac{a\times c\times x}{b+d+1}\le\dfrac{a}{b}\) 的话，就有 \(d+1+b\ge c\times x\times b\) 否则肯定直接选 \(\dfrac{a}{b}\) 更优。

​ 再与 \(\dfrac{c}{d}\) 比较，得出相似的一条式子 \(d+1+b\ge a\times x\times d\)。两式左右分别相加，得到 \(2\ge (c\times x-2)\times b+(a\times x-2)\times d\) 。又因为 \(b,d\ge 1\) 所以 \(c\times x,a\times x\le 3\)。

​ 但是注意到， \(c\times x,a\times x\) 能取到 \(3\) 是因为原不等式带等号，取 \(3\) 的时候可能会使这个不等式满足等于号而成立。但是我们选答案的范围是整张图，如果取等号的话，为什么不直接取魔力值为 \(\dfrac{a}{b}\) 或者 \(\dfrac{c}{d}\) 作为答案呢？

​ 所以我们尝试把不等式的等号去掉就得到 \(c\times x,a\times x\le2\) 。由于 \(a,c,x\) 均为正整数，那么 \(a,c,x\) 只能为 \(1,2\)。接下来分类讨论

• \(x=2\) 的情况。

  那么 \(a,c\) 都只能为 \(1\)。那么就有 \(\dfrac{1}{b},\dfrac{1}{d},\dfrac{2}{b+d+1}\) 这 \(3\) 种情况。如果拼起来更优的\(\dfrac{2}{b+d+1}<\dfrac{2}{2\times b}\) 且 \(\dfrac{2}{b+d+1}<\dfrac{2}{2\times d}\)。所以当且仅当 \(b=d\) 时，拼起来会更优，也就是 \(x\) 这个点连接了两条长度一样，点权全为 \(1\) 的链。这对标我们的结论 \(2\)。

• \(x=1\) 的情况。

  首先如果 \(a,c\) 都为 \(1\)。那么拼起来是更优的，对标结论 \(1\)。如果 \(a,c\) 之中有一个是 \(2\) 。就说明拼起来的路径中只有一个点权是 \(2\)。根据我们刚刚推导的情况，一条路径上只有一个点权为 \(2\) 时。当且仅当这个点处于路径中心时拼接起来更优（即结论 \(2\)）。

  最后一种情况：\(a,c\) 都为 \(2\)。也就是这条链上有 \(2\) 个权值为 \(2\) 的点的情况。 那么我们设这两个权值为 \(2\) 的点将总长度为 \(b+d+1\) 的路径划分成了 \(3\) 条只包含点权为 \(1\) 的点的链，它们的长度分别为 \(u,v,p\)。那么可能的最小的权值情况就为 \(\dfrac{1}{\max(u,v,p)},\dfrac{4}{b+d+1},\dfrac{2}{u+v+1},\dfrac{2}{v+p+1}\)。直接对比 \(\dfrac{1}{max(u,v,p)},\dfrac{4}{u+v+p+2}\)。 得 \(4\times\max(u,v,p)<u+v+p+2\)，当且仅当 \(u,v,p\) 全为 \(1\) 时成立。那么这 \(4\) 个可能的值就全是具体的了。分别是 \(\dfrac{1}{1},\dfrac{4}{5},\dfrac{2}{3},\dfrac{2}{3}\) ，显然 \(\dfrac{2}{3}<\dfrac{4}{5}\)，所以拼接起来一定不是最优的。（可以结合下图理解）

  

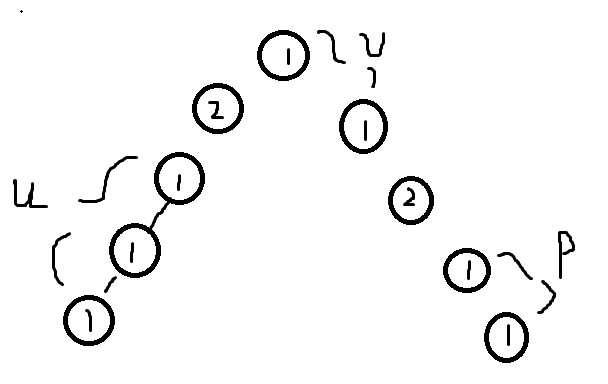
​ 综上所述，我们在文章一开始提出的三个结论成立。

---

解题：

​ 知道了结论，我们就可以根据结论进行求解了，那么我们要找的就是两种链。第一种是点权全是 \(1\) 的。第二种是权值为 \(2\) 的点在链中心的。

​ 找链的工作可以使用树形 dp 来求解。关于树形 dp 的写法网上已经有很多题解了。这里介绍一种点分治的写法。

​ 首先是关于全是 \(1\) 的链的求解，那么我们寻找路径是就只要遍历点权为 \(1\) 的点。然后维护路径最大值与次大值（注意最大值与次大值不能在同一子树内）。局部代码如下：

void Get_dis(int p,int fa,int d)
{
	if(val[p]!=1) return ;//点权不是1不用记录到数组内
	arr[++cnt]=d;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(to==fa||vis[to]) continue;
		Get_dis(to,p,d+1);
	}
}
void solve(int p)
{
	int mx[2]={},tmp=0,id[2];id[0]=id[1]=-1;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		cnt=0;Get_dis(to,p,1);tmp=0;
		for(int j=1;j<=cnt;++j)
			tmp=max(tmp,arr[j]);//维护子树最大值
		if(tmp>mx[1])//维护最大值与次大值
			mx[1]=tmp;id[1]=i;
		if(mx[1]>mx[0])
		{
			swap(mx[1],mx[0]);
			swap(id[1],id[0]);
		}
		ans=max(ans,mx[0]+mx[1]+1);//用不在同一子树内的最大值次大值更新答案
	}
}

​ 同时的，Get_dis 这个函数还可以在获取当前解决的点（当前解决子树的重心）点权为 \(2\) 时需要的路径，然后我们维护一下最长的两条相等的路径即可，可以通过以下方式实现。

struct Data
{
	int x,y;//x是分子，y是分母
	bool operator <(const Data&a) const
	{
		return x*1.0/y<(a.x*1.0/a.y);
	}
	void print()
	{
		int d=gcd(x,y);
		printf("%d/%d\n",x/d,y/d);
	}
}res;
void solve_(int p)
{
	int mx=0;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		cnt=0;Get_dis(to,p,1);
		for(int j=1;j<=cnt;++j)//因为两个链的长度要相等，所以取较小值更新答案。
			res=min(res,(Data){2,min(mx,arr[j])*2+1});
		for(int j=1;j<=cnt;++j)//维护一下已经遍历到的最大值
			mx=max(mx,arr[j]);
	}
}

​ 但是有一种可能，我们在解决的点点权是 \(1\) 但是我们获取的链的长度里面有点权为 \(2\) 的点，如下图这种情况，\(p\) 是我们目前处理的点（当前处理子树的重心）。

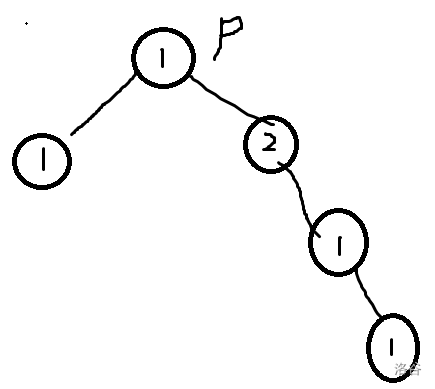
​ 所以我们还得再写一个类似 Get_dis 的函数用来获取带一个点权为 \(2\) 的点的路径。如下：

void Get_dis2(int p,int fa,int d,int d2,int c)
{
	if(val[p]!=1&&val[p]!=2) return ;
	if(c>2) return ;
	dis[++all]={d,d2};//这里的dis数组是data类型，但只是为了存储两个值，可以用pair替代。
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(to==fa||vis[to]) continue;
		Get_dis2(to,p,c==2?d:d+1,c==2?d2+1:d2,c*val[p]);
	}
}

​ 至于根据路径求解的代码，由于当前处理的点（处理子树的重心）的点权是 \(1\) 我们可以将它与上面的 solve（处理全是 \(1\) 的链的函数）合并一下。就变成了下面这个代码：

void solve(int p)
{
	int mx[2]={},tmp=0,id[2];id[0]=id[1]=-1;//下面这部分展示过了，可以跳过。
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		cnt=0;Get_dis(to,p,1);tmp=0;
		for(int j=1;j<=cnt;++j)
			tmp=max(tmp,arr[j]);
		if(tmp>mx[1])
			mx[1]=tmp;id[1]=i;
		if(mx[1]>mx[0])
		{
			swap(mx[1],mx[0]);
			swap(id[1],id[0]);
		}
		ans=max(ans,mx[0]+mx[1]+1);
	}//上面这部分展示过了，可以跳过。
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		all=0;Get_dis2(to,p,val[to]==1?1:0,0,val[to]);
		for(int j=1;j<=all;++j)
		{
			int d1=dis[j].x,d2=dis[j].y;//一样，由于全为1的链的长度需要相等，取较小值。
			res=min(res,Data{2,min((i==id[0]?mx[1]:mx[0])+1+d1,d2)*2+1});
		}
	}
}

​ 上述问题到这里就解决了，总时间复杂度为 \(O(n\log(n))\)。加大常数。

​ 全部代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 1e6+5;
int n,dp[MAXN],siz[MAXN],Tsiz,root,cnt,arr[MAXN],ans,val[MAXN],all;
bool vis[MAXN];
vector <int> e[MAXN];
int gcd(int x,int y)
{
	if(y==0) return x;
	return gcd(y,x%y);
}
void Get_root(int p,int fa)
{
	dp[p]=0;siz[p]=1;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(to==fa||vis[to]) continue;
		Get_root(to,p);
		siz[p]+=siz[to];
		dp[p]=max(siz[to],dp[p]);
	}
	dp[p]=max(dp[p],Tsiz-siz[p]);
	if(dp[p]<dp[root]) root=p;
}
struct Data
{
	int x,y;//x表示分子，y表示分母
	bool operator <(const Data&a) const
	{
		return x*1.0/y<(a.x*1.0/a.y);
	}
	void print()
	{
		int d=gcd(x,y);
		printf("%d/%d\n",x/d,y/d);
	}
}res,dis[MAXN];
void Get_dis(int p,int fa,int d)
{
	if(val[p]!=1) return ;
	arr[++cnt]=d;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(to==fa||vis[to]) continue;
		Get_dis(to,p,d+1);
	}
}
void Get_dis2(int p,int fa,int d,int d2,int c)
{
	if(val[p]!=1&&val[p]!=2) return ;
	if(c>2) return ;
	dis[++all]={d,d2};
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(to==fa||vis[to]) continue;
		Get_dis2(to,p,c==2?d:d+1,c==2?d2+1:d2,c*val[p]);
	}
}
void solve(int p)
{
	int mx[2]={},tmp=0,id[2];id[0]=id[1]=-1;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		cnt=0;Get_dis(to,p,1);tmp=0;
		for(int j=1;j<=cnt;++j)
			tmp=max(tmp,arr[j]);
		if(tmp>mx[1])
			mx[1]=tmp;id[1]=i;
		if(mx[1]>mx[0])
		{
			swap(mx[1],mx[0]);
			swap(id[1],id[0]);
		}
		ans=max(ans,mx[0]+mx[1]+1);
	}
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		all=0;Get_dis2(to,p,val[to]==1?1:0,0,val[to]);
		for(int j=1;j<=all;++j)
		{
			int d1=dis[j].x,d2=dis[j].y;
			res=min(res,Data{2,min((i==id[0]?mx[1]:mx[0])+1+d1,d2)*2+1});
		}
	}
}
void solve_(int p)
{
	int mx=0;
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		cnt=0;Get_dis(to,p,1);
		for(int j=1;j<=cnt;++j)
			res=min(res,(Data){2,min(mx,arr[j])*2+1});	
		for(int j=1;j<=cnt;++j)
			mx=max(mx,arr[j]);
	}
}
void Divide(int p)
{
	vis[p]=1;
	if(val[p]==1) solve(p);
	if(val[p]==2) solve_(p);
	for(int i=0;i<e[p].size();++i)
	{
		int to=e[p][i];
		if(vis[to]) continue;
		Tsiz=siz[to];root=0;
		Get_root(to,p);
		Divide(root);
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;++i)
	{
		int u,v;
		scanf("%d %d",&u,&v);
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(int i=1;i<=n;++i)
		scanf("%d",&val[i]);
	dp[root=0]=n+1;Tsiz=n;ans=-1;res.y=1;res.x=1e9;
	Get_root(1,0);
	Divide(root);
	if(ans!=-1)
	{
		if(Data{1,ans}<res)
			printf("1/%d\n",ans);
		else res.print();			
	}
	else
	{
		if(res.x!=1e9)
		{
			res.print();
		}
		else
		{
			ans=1e9;
			for(int i=1;i<=n;++i)
				ans=min(ans,val[i]);
			printf("%d/1\n",ans);			
		}
	}
	return 0;
}

总结：点分治，解决树上路径的一种优秀方法。（虽然在这题并不优秀）