POI 2010 MOT-Monotonicity 2
POI 2010 MOT-Monotonicity 2
题目链接:POI2010 MOT-Monotonicity 2
考虑 dp,二维 dp 十分好想,但是二维 dp 无论怎么优化最快也只能达到 \(O(n\times k\times\log(n))\),那么二维 dp 的想法只能被舍弃,我们肯定立马想到不用二维,设 \(f_i\) 表示以 \(i\) 为结尾的,所能形成满足条件的最长子序列的长度。可是这么定义状态能不能满足最优子结构这个性质呢。
如果满足最优子结构这个性质,就说明从最优解转移一定不比非最优解转移劣。
下面我们证明这个状态满足最优子结构:
我们采取反证法,假设现在我们正在求 \(f_i\)。\(\forall j\in[1,i-1]\),我们假设 \(f_j=x\),和一个比 \(x\) 短,以 \(j\) 为结尾的序列结尾再添上一个 \(i\) 就构成了长度为 \(f_i\) 的序列。即 \(f_i\) 不是由 \(f_j\) 这个最优解添上一个 \(i\) 获得的,而是由一个长度为 \(y\) 的非最优解序列获得的。那么根据我们的假设,有 \(x>y\)。我们设 \(\text{long}\) 序列为长度为 \(x\) 的,以 \(j\) 为结尾的最优解序列,\(\text{short}\) 序列为长度为 \(y\) 的,以 \(j\) 为结尾的非最优解序列,那么假设就是 \(f_i\) 是由 \(i\) 继承 \(\text{short}\) 序列得到序列的长度 ,而且 \(f_i\) 从某个最优解转移来的答案劣于由 \(\text{short}\) 转移来的答案。
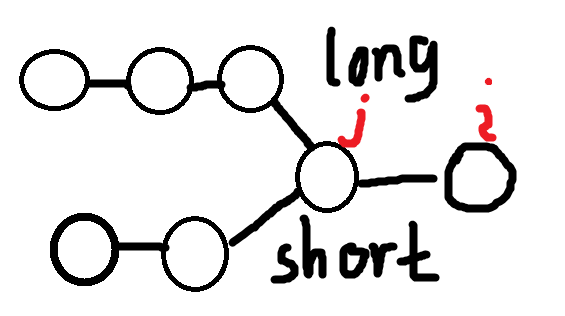
那么根据假设我们有 \(f_i=y+1,x>y\)。同时还有以下推论:
-
位置 \(x\) 与 位置 \(y\) 的符号不同。
如果他们相同的话,由于两个位置上的数值同为 \(a_j\) 那么 \(\text{long}\) 序列可以替代 \(\text{short}\) 序列,因为如果 \(a_i\) 能接在 \(\text{short}\) 后面就一定能接在 \(\text{long}\) 后面,而 \(x+1>y+1\) 显然,使用 \(\text{long}\) 序列更优,所以如果我们要满足我们的假设,\(a_i,a_j\) 就只能满足 \(y\) 后的符号而不满足 \(x\) 后的符号。
-
\(a_i\) 与 \(a_j\) 不相等。
如果相等,我们继续分类讨论,若 \(x\) 后符号为 \(\text{=}\) 则选 \(\text{long}\) 序列转移。若 \(x\) 后符号不为 \(\text{=}\) 由于 \(a_i=a_j\) 那么我们可以用 \(a_i\) 代替 \(a_j\) 得到一个长度为 \(x\) 的序列,即通过 \(\text{long}\) 里 \(j\) 的前一个转移过来,而 \(x\ge y+1\) 所以 \(a_i=a_j\) 时,从最优解转移一定不劣。
-
位置 \(y\) 的位置不是 \(\text{=}\)。
根据上述两推论得到。
那么不满足上述推论的情况就可以从最优解转移,我们继续探讨满足上述三种推论的情况。
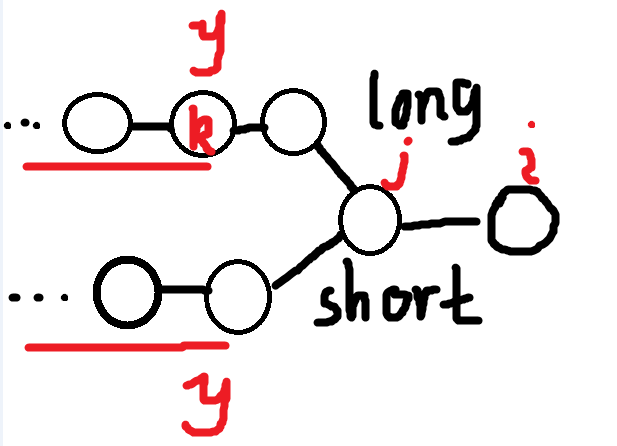
由于 \(x>y\) 所以在 \(\text{long}\) 序列里,我们可以找到一个节点 \(k\) 使得 \(f_k=y\)。这样我们又有结论:
-
\(a_i,a_k\) 不能满足 \(y\) 位置后符号的关系。
如果满足,那么从 \(f_k\) 转移过来的答案不劣于 \(\text{short}\) 转移过来的答案,这与我们的假设不符。
-
如果 \(x\) 位置的符号是 \(\text{<}\),那么 \(y\) 位置的符号只能是 \(\text{>}\)。
因为根据之前的推论 \(x,y\) 位置符号不同,且 \(y\) 位置的符号不能是 \(\text{=}\) 号。
然后我们顺着这种情形推下去,得到 \(a_k<a_i<a_j\) (\(a_k,a_i\) 不满足符号而 \(a_i,a_j\) 满足),又因为位置 \(y\) 的符号是 \(\text{>}\)。那么存在一个 \(a_l(k<l\le j)\) 且 \(l\) 后的符号一定是 \(\text{<}\),如果没有一个 \(l\) 后的符号是 \(\text{<}\) 那么 \(a_k,a_j\) 的关系应该是 \(a_k\ge a_i\)。这与上述情况相违背。那么既然存在这样的 \(l\),那我们取第一次出现的 \(l\) 就能保证 \(l\) 前的符号都是 \(\text{>},\text{=}\),就有 \(a_k\ge a_l<a_j\) 即 \(a_l<a_k<a_i<a_j\),又 \(l\) 后的符号为 \(\text{<}\) 那么 \(f_i\) 可以由 \(f_l\) 转移来,而 \(f_l\ge f_k+1=y+1\),所以 \(f_i\ge y+2>y+1\)。因此在这种情况中,\(f_i\) 从某个最优解转移过来反而更优。
-
如果 \(x\) 位置的符号是 \(\text{=}\),那么 \(y\) 位置的符号只能是 \(\text{>},\text{<}\)。
先看 \(y\) 位置为 \(\text{>}\) 的情况。发现这种情况于上述情况相同(因为在上面那种情况的推导中 \(x\) 位置的符号没有出现)。
再看 \(y\) 位置为 \(\text{<}\) 的情况(其实这里与上面那个情况刚好相反,将上述推导符号反一反就可以得到,这里有兴趣的读者可以看,因为过程雷同也可以跳过)
有 \(a_k>a_i>a_j\) (\(a_k,a_i\) 不满足而 \(a_i,a_j\) 满足),又 \(y\) 位置的符号是 \(\text{<}\) 那么一定存在 \(a_l(k<l\le j)\) 满足 \(l\) 位置后的符号为 \(\text{>}\),否则 \(a_k,a_j\) 的关系应该是 \(a_k\le a_j\) 这与上述情况不符。所以 \(l\) 一定存在,我们取第一次出现的 \(l\),就能满足 \(l\) 前的符号全是 \(\text{<},\text{=}\) 那么有 \(a_k\le a_l>a_i\),又 \(l\) 后的符号是 \(\text{>}\),那么 \(f_i\) 可以由 \(f_l\) 转移而来,而 \(f_l\ge f_k+1\ge y+1\),则 \(f_i\ge y+2>y+1\) ,那么这种情况下也是用最优解转移过来更优。
-
如果 \(x\) 位置的符号是 \(\text{>}\) 那么 \(y\) 位置的符号只能是 \(\text{<}\) 这与上述情况一致(因为 \(x\) 位置的符号没有在推导出现,也就没有影响)
综上所述,\(f_i\) 从之前的最优解转移过来的答案一定不劣,甚至更优。那么有一个显然的 \(O(n^2)\) 的 dp。转移式为:
然后取个极值就好了。那么优化也是显然的,我们开两个树状数组,分别记录前缀最大值和后缀最大值,然后用数组记录一下相等的权值的 \(dp_i\) 的最大值。这题的主要难点就是想到一维 dp 的可行性。
代码如下:
#include<bits/stdc++.h>
#define lowbit(i) (i&(-i))
using namespace std;
const int MAXN = 5e5+5;
const int MX = 1e6;
int n,k,a[MAXN],b[MAXN];
int t1[MX+5],t2[MX+5],dp[MAXN],val[MX+5];
void upd(int *t,int pos,int x){for(int i=pos;i<=MX;i+=lowbit(i))t[i]=max(t[i],x);}
int query(int *t,int pos){int ans=0;for(int i=pos;i;i-=lowbit(i))ans=max(ans,t[i]);return ans;}
stack <int> st;
int main()
{
scanf("%d %d",&n,&k);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
for(int i=1;i<=k;++i)//1 = ,0 < , 2 >
{
char s[4];
scanf("%s",s+1);
if(s[1]=='<') b[i]=0;
else if(s[1]=='=') b[i]=1;
else b[i]=2;
}
for(int i=k+1;i<=n;++i)
b[i]=b[i-k];
int ans=0,res=0;
for(int i=1;i<=n;++i)
{
dp[i]=max(val[a[i]],max(query(t1,a[i]-1),query(t2,MX-a[i])))+1;
if(b[dp[i]]==0)upd(t1,a[i],dp[i]);
if(b[dp[i]]==2)upd(t2,MX-a[i]+1,dp[i]);
if(b[dp[i]]==1)val[a[i]]=max(dp[i],val[a[i]]);
}
int ind=0;
for(int i=1;i<=n;++i)
if(dp[i]>ans) ans=dp[i],res=a[i],ind=i;
printf("%d\n",ans);--ans;st.push(res);
for(int i=ind-1;i>=1;--i)//输出,从尾部往前遍历数组,利用栈的特性。
{
if(ans==0) break;
if(b[ans]==1)
{
if(res==a[i]&&dp[i]==ans)
{
st.push(a[i]);
--ans;
res=a[i];
}
}
else if(b[ans]==0)
{
if(res>a[i]&&dp[i]==ans)
{
st.push(a[i]);
--ans;
res=a[i];
}
}
else if(b[ans]==2)
{
if(res<a[i]&&dp[i]==ans)
{
st.push(a[i]);
--ans;
res=a[i];
}
}
}
while(!st.empty())
{
printf("%d ",st.top());
st.pop();
}
return 0;
}
总结:太折磨了,鬼知道我考试被这个苟证明卡了多久,最后还是看题解才会的。。。

