[SHOI2014]概率充电器

[SHOI2014]概率充电器

​ 题目链接:[SHOI2014]概率充电器

---

​ 一眼期望dp。然而并不是的。显然答案应该是：

\[\sum_{i=1}^{n}{p_i*w_i} \]

​ 注意到，\(w_i\) 在本题中为1，那么答案就是所有概率的累加（于是我成功在模拟赛的最后10min才发现这点，之前都在傻傻的转移期望）所以我们只要求概率就好了。

​ 这题求期望比较复杂，但是概率并不难求。值得一提的是，这题中如果是因为别人通电导致自己通电的充电元件也可以使别的充电元件充电。

​ 题目给出的结构是树形结构，那么我们就用树形dp来解决这个问题，我们设 \(dp_i\) 为 \(i\) 这个点通电的概率，可是这个比较难求，因为只要它的儿子中有一个能通电且边通电他就能通电。正难则反，我们可以求出 \(i\) 这个点不通电的概率，这个比较好求，所以我们设 \(dp_i\) 为 \(i\) 不通电的概率。那么转移方程式如下：

\[\begin{aligned} dp_{cur}&=\sum_{i=1}^{k}{(1-w)\times dp_i+(1-w)\times(1-dp_i)+w\times dp_i} \\ &=\sum_{i=1}^{k}{dp_i\times w+(1-w)*(1-dp_i)} \end{aligned} \]

​ 其中 \(i\) 为儿子节点，而 \(cur\) 为现在的节点。

​ 这部分dp转移的代码如下：

void pre_dfs(int cur,int fa)
{
	double all=(1.0-v[cur]);
	for(int i=head[cur];i;i=e[i].pre)
	{
		int to=e[i].to;double w=e[i].w;
		if(to==fa) continue;
		pre_dfs(to,cur);
		all*=(dp[to]+(1.0-dp[to])*(1.0-w));
	}
	dp[cur]=all;
}

​ 那么我们做一次树形dp就求出来了，但是我们会发现，其实这么求出来的 \(dp\) 值只有根节点是正确的，因为对于一个节点来说，它的父亲节点是否通电对它是否通电也有影响。而在树中，只有根节点没有父亲，所以只有根节点的概率是对的。那我们怎么办呢？最无脑的办法就是再做 \(n\) 遍，但是这样我们的时间是 \(O(n^2)\) 的。那么我们可以考虑换根dp。

​ 我们设 \(f_i\) 为 \(i\) 是根节点时 \(i\) 不通电的概率。那么我们可以从 \(i\) 父亲节点转移过来。如果根节点从 \(i\) 的父亲节点转移到 \(i\) 的话，那么 \(f_{fa}/((1-dp[i])*w+dp[i])\) 就是 \(i\) 为根节点时它父亲所在子树的根节点的概率。这条方程式是根据我们上面推来的式子的到的。画个图吧。

​

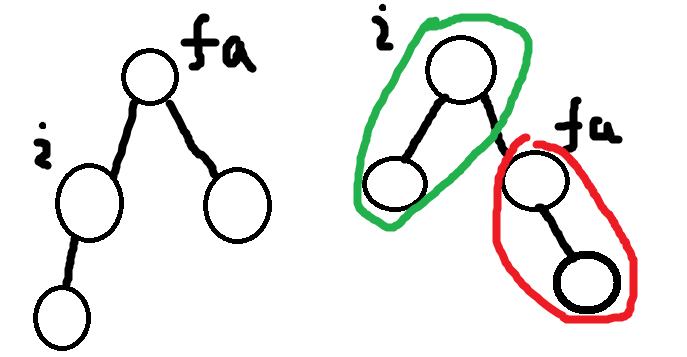
​ 我们设 \(tmp=f_{fa}/((1-dp[i])*w+dp[i])\)。那么 \(tmp\) 实际上就是 \(fa\) 在红色部分这棵子树中 \(fa\) 为根节点时 \(fa\) 不被充电的概率，而我们先前推出的 \(dp_i\) 就是绿色部分这棵子树中根节点为 \(i\) 时 \(i\) 不被充电的概率。接下来的转移方程式就呼之欲出了：

\[f_i=dp_i\times(tmp+(1-w)*(1-tmp)) \]

​ 换根dp的代码如下：

void dfs(int cur,int fa)
{
	for(int i=head[cur];i;i=e[i].pre)
	{
		int to=e[i].to;double w=e[i].w;
		if(to==fa) continue;
		double tmp=f[cur]/((1.0-w)*dp[to]+dp[to]*w+(1.0-dp[to])*(1.0-w));
		f[to]=dp[to]*(tmp+(1.0-tmp)*(1.0-w));
		dfs(to,cur);
	}
}

​ 那么我们的答案就是:

\[\sum_{i=1}^{n}{f_i} \]

​ 显然，每个点只会在树形dp和换根时都只会分别遍历过一遍，所以时间复杂度为 \(O(n)\)。

​ 全部代码如下：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5e5+5;
int tot_E,n,head[MAXN];
struct E
{
	int to,pre;
	double w;
}e[MAXN<<1];
void add(int u,int v,double w)
{
	e[++tot_E]=E{v,head[u],w};
	head[u]=tot_E;
}
double dp[MAXN],v[MAXN],d[MAXN],f[MAXN];
void pre_dfs(int cur,int fa)
{
	double all=(1.0-v[cur]);
	for(int i=head[cur];i;i=e[i].pre)
	{
		int to=e[i].to;double w=e[i].w;
		if(to==fa) continue;
		pre_dfs(to,cur);
		all*=(dp[to]+(1.0-dp[to])*(1.0-w));
	}
	dp[cur]=all;
}
void dfs(int cur,int fa)
{
	for(int i=head[cur];i;i=e[i].pre)
	{
		int to=e[i].to;double w=e[i].w;
		if(to==fa) continue;
		double tmp=f[cur]/((1.0-w)*dp[to]+dp[to]*w+(1.0-dp[to])*(1.0-w));
		f[to]=dp[to]*(tmp+(1.0-tmp)*(1.0-w));
		dfs(to,cur);
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;++i)
	{
		int a,b,p;
		scanf("%d %d %d",&a,&b,&p);
		add(a,b,(double)(p*1.0)/100.0);
		add(b,a,(double)(p*1.0)/100.0);
	}
	for(int i=1;i<=n;++i)
	{
		int q;
		scanf("%d",&q);
		v[i]=(double)(q*1.0)/(100.0);
	}
	pre_dfs(1,0);
	f[1]=dp[1];
	dfs(1,0);
	double ans=0;
	for(int i=1;i<=n;++i)
		ans+=(1.0-f[i]);
	printf("%.6lf",ans);
	return 0;
}

总结：概率期望dp还是比较考验思维能力的，我给这题跪下了，还是太菜了。