[USACO09JAN]Safe Travel G
[USACO09JAN]Safe Travel G
题目链接:[USACO09JAN]Safe Travel G
又是一道初见杀的题目,这道题是跟最短路树有关。何为最短路树?
考虑一个连通无向图 \(G\),一个顶点 \(v\) 为根节点的最短路径树 \(T\) 是图 \(G\) 满足下列条件的生成树——树 \(T\) 中从根节点 \(v\) 到其他顶点 \(u\) 的路径距离,在图 \(G\) 中是 \(v\) 到 \(u\) 的最短路径距离。
这个定义还是比较好理解的,那么我们怎么构造出最短路径树呢?既然跟最短路有关,我们先用 Dijkstra 算法预处理出图 \(G\) 中 \(v\) 节点到其他所有顶点 \(u\) 的最短距离。然后对于一条边 \(E\) 设它两端的节点为 \(x,y\),边权值为 \(w\) 如果 \(dis_x+w=dis_y\) 就说明在最短路径树中 \(x\) 是 \(y\) 的父亲节点。这样在本题中是正确的。因为据题意描述,根节点 \(v\) 到任意一个顶点 \(u\) 的路径是唯一的。这么连,首先它是连通的,因为每个节点的最短路径都是存在的。其次,一共有 \(n\) 个节点,我们对除了根节点 \(v\) 外的每个节点都找了一个父亲,所以有 \(n-1\) 条边。那么我们这么构造出来的就是一棵最短路径树了。
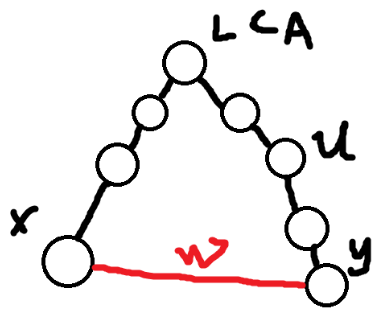
构造出一棵最短路径树后,我们来试着添加无用边,这里的无用边指的是题目中给出,但最短路径树中没用到的边。首先看下图。
图中的红边是一条无用边。边权为 \(w\),而两端节点为 \(x,y\) 我们来考虑下怎么更新 \(u\) 点的答案。如果要更新 \(u\) 点的话那么只能通过无用边走过去。通过最短路径树的定义可知。从根节点到一个顶点 \(u\) 的距离为 \(dis_u\)。那么我们可以通过这个性质可知,\(u\) 到 \(y\) 的距离就为 \(dis_y-dis_u\)。那么我们就可以得知:
所以我们可以知道,我们可以用这条边,将图中这个环所有的除了 LCA 外的点全部更新。为什么LCA不能更新呢,因为 LCA 最短路径的最后一条边不在这个子树里了。
但是这么更新我们的时间是肯定承受不住的。因为我们重复更新了许多点。那能不能让每个点只更新一次呢,我们考虑将边排序,对于更新的点 \(u\) 来说 \(dis_u\) 是不变的,我们考虑对于每条边\(E\),它两边的节点为 \(x,y\),边权为 \(w\)。我们按照 \(dis_x+dis_y+w\) 从小到大进行排序,这样我们使得每个点在第一次更新时就是它的最小值。
但是我们在更新时,依然会遍历无用的点导致时间复杂度丝毫没有下降,那么我们得跳过已经更新过的点,这个时候我们可以使用一个常规的套路并查集缩点。
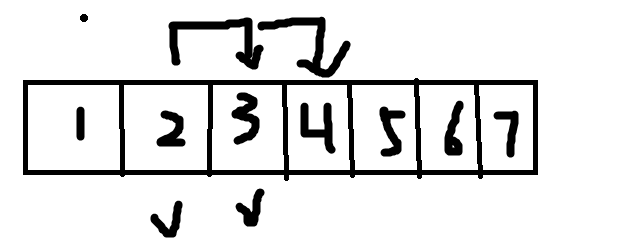
考虑一个一维数组,我们将遍历过一次的点 \(i\) 的祖先设为 \(i+1\)。然后每次访问我们都访问这个节点的祖先,效果像图中所示,假设 2,3都已经被遍历过,我们从1开始遍历,遍历到2时,由于访问的是它的祖先节点,所以直接会跳到4去,这样我们就实现了不重复遍历的目的。
一维数组并查集缩点伪代码如下:
for(int i=1;i<=n;i=find(i+1))
{
.....//操作
f[i]=i+1;
}
并查集缩点的优势就在于多次遍历同一段不会重复,我们将一维数组想像成一条链运用在树上,这题就成了,树上并查集缩点代码如下:
for(int i=1;i<=m;++i)
{
int u=edge[i].u,v=edge[i].v,w=edge[i].w;
if(dis[u]+w==dis[v]||dis[v]+w==dis[u]) continue;
int x=find(u),y=find(v);
while(x!=y)
{
if(dep[x]<dep[y]) swap(x,y);
ans[x]=dis[u]+dis[v]+w-dis[x];
f[x]=fa[x];
x=find(x);
}
}
如果 \(x\) 直接跳到 LCA 上面了会不会有问题呢?实际上并不会, \(x\) 跳到 LCA 上面说明 LCA 已经更新过了,这时候另一个点跳到 LCA 时就会与 \(x\) 重合。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;
const int MAXM = 2e5+5;
const int INF = 0x3f3f3f3f;
int tot_E,head[MAXN],fa[MAXN],f[MAXN],dep[MAXN];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
struct E
{
int to,w,pre;
}e[MAXM<<1];
void add(int u,int v,int w)
{
e[++tot_E]=E{v,w,head[u]};
head[u]=tot_E;
}
int dis[MAXN],n,m,ans[MAXN];
bool vis[MAXN];
struct node
{
int p,dis;
bool operator < (const node &x)const
{
return dis>x.dis;
}
};
struct Edge
{
int u,v,w;
bool operator < (const Edge &x)const
{
return dis[u]+dis[v]+w<(dis[x.u]+dis[x.v]+x.w);
}
}edge[MAXM<<1];
void dij()
{
priority_queue <node> q;
q.push(node{1,0});
memset(dis,0x3f,sizeof dis);
dis[1]=0;
while(!q.empty())
{
int p=q.top().p,dism=q.top().dis;
q.pop();
if(vis[p]) continue;
vis[p]=1;
for(int i=head[p];i;i=e[i].pre)
{
int to=e[i].to,w=e[i].w;
if(dis[to]>dism+w)
{
dis[to]=dism+w;
q.push(node{to,dis[to]});
}
}
}
}
void dfs(int cur ,int father)
{
fa[cur]=father;dep[cur]=dep[father]+1;
for(int i=head[cur];i;i=e[i].pre)
{
int to=e[i].to,w=e[i].w;
if(to==father||dis[cur]+w!=dis[to]) continue;
dfs(to,cur);
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;++i)
{
int a,b,t;
scanf("%d %d %d",&a,&b,&t);
add(a,b,t);add(b,a,t);
edge[i].u=a,edge[i].v=b,edge[i].w=t;
}
memset(ans,0x3f,sizeof ans);ans[1]=0;
dij();
dfs(1,0);
sort(edge+1,edge+1+m);
for(int i=1;i<=n;++i) f[i]=i;
for(int i=1;i<=m;++i)
{
int u=edge[i].u,v=edge[i].v,w=edge[i].w;
if(dis[u]+w==dis[v]||dis[v]+w==dis[u]) continue;
int x=find(u),y=find(v);
while(x!=y)
{
if(dep[x]<dep[y]) swap(x,y);
ans[x]=dis[u]+dis[v]+w-dis[x];
f[x]=fa[x];
x=find(x);
}
}
for(int i=2;i<=n;++i)
printf("%d\n",ans[i]==INF?-1:ans[i]);
return 0;
}
总结:最短路径树,普及组的知识点我居然第一次听到,还是见识狭小了 。以及在别的博客看到一句话还是比较有用的:如果题目给出最短路径唯一,那么十有八九与最短路径树有关。