[USACO12DEC]First! G

[USACO12DEC]First! G

​ 题目链接：https://www.luogu.com.cn/problem/P3065

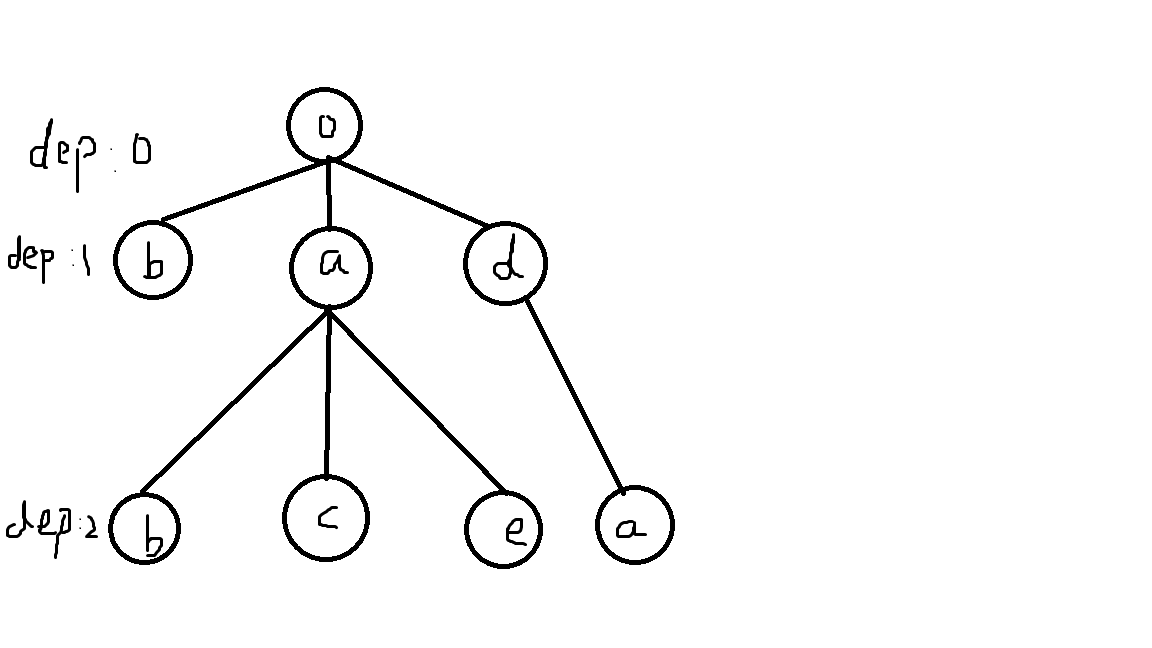
​ 看到字典序，想到的东西必然是 trie树 。我们将 \(n\) 个字符串全部插入 trie树 中，然后对于每一个字符串我们怎么检查是否能排在第一个呢。对于一个字符串，我们从头开始爬，想象一棵 trie树。如下图所示：

​ 假设我们需要判断 ac 这个字符串能不能排在第一个。首先对于第0层，我们要走到 \(a\)，所以在 0 的子树下面我们将 a 向其他在 0 子树下，同一层的节点（即 \(b,d\)）连一条边，表示在我们设立的字典序中 \(a<b,a<d\) 。然后我们走到 \(a\) 这个节点，然后我们的目标是 \(c\)，那么就让 \(c\) 对 \(a\) 得子树下，同一层的其他存在的字母（\(b,e\)） 连一条边。注意，这里不用对同是第二层的 \(a\) 连，因为它不在第一层 \(a\) 的子树当中，在我们设定 \(a<b,a<d\) 时，它所在字符串的字典序就已经比 ac 这个字符串要大了。最后我们走到 \(c\)。然后停止。

​ 我们得到一个图，这个图描绘了大小关系，如果这个图的大小关系成立的话，那么这个字符串就能够通过改变字母表的顺序来让它的字典序最小。如何判断这个图的大小关系是否成立呢？我们只需判断这个图中是否有环就够了。有环，则不成立。那么为什么满足这幅图的大小关系就行了呢，毕竟这幅图描绘的大小关系并不完整。因为通过我们在 trie树 上的操作，如果这幅图的大小关系满足了，这个字符串是一定能排到第一位的。对于其他的每个字符串，字典序的大小肯定是它们从左往右第一个不同的字符进行比较得到的。从左往右的第几位，相当于 trie树 中第几层，而我们的关系使得当前字符串的每一个字符在它所对应的那层中都是第一小的。这幅图描绘的大小关系不完整也没关系，因为我们只要判断这个字符串能不能排到第一小，至于其他的大小关系，构造一种合法情况就好了，比如把后面一串没排的接在已知最大的后面。

​ 还有一个小细节，就是如果 \(n\) 个字符串中存在一个字符串的前缀，那么这个字符串肯定不能排到第一个。

​ 总时间复杂度 \(O(26\times m)\)。（\(m\) 表示字符总数）

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3e5+5;
string s[30005];
int n;
struct Trie
{
	int tot,to[MAXN][27],exist[MAXN],in[30];
	vector <int> e[27];
	void init()
	{
		memset(in,0,sizeof in);
		for(int i=0;i<=26;++i) e[i].clear();
	}
	void insert(string s)
	{
		int now=0;
		for(int i=0;i<s.size();++i)
		{
			int num=s[i]-'a';
			if(to[now][num]==0) to[now][num]=++tot;
			now=to[now][num];
		}
		exist[now]=1;
	}
	bool check(string s)
	{
		int now=0;
		for(int i=0;i<s.size();++i)
		{
			int num=s[i]-'a';
			if(exist[now]) return false;
			for(int j=0;j<26;++j)
				if(to[now][j]!=0&&j!=num)
					e[num].push_back(j),in[j]++;
			now=to[now][num];
		}
		queue <int> q;
		for(int i=0;i<26;++i) if(!in[i]) q.push(i);
		while(!q.empty())
		{
			int p=q.front();
			q.pop();
			for(int i=0;i<e[p].size();++i)
			{
				int to=e[p][i];
				in[to]--;
				if(!in[to]) q.push(to);
			}
		}
		for(int i=0;i<26;++i) if(in[i]) return false;
		return true;
	}
}t;
bool ans[30005];
int main()
{
	std::ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;++i)
	{
		cin>>s[i];
		t.insert(s[i]);
	}
	int cnt=0;
	for(int i=1;i<=n;++i)
	{
		t.init();
		if(t.check(s[i])) ans[i]=1,cnt++;	
	}
	cout<<cnt<<"\n";
	for(int i=1;i<=n;++i)
		if(ans[i]) cout<<s[i]<<"\n";
	return 0;
}