6.3 树和森林
数的存储结构(表示法)、森林与二叉树的转换、
树和森林的遍历、哈夫曼树
树的存储结构
双亲表示法
取一块连续的内存空间,在存储每个结点的同时,各自都附加一个记录其双亲结点位置的变量。
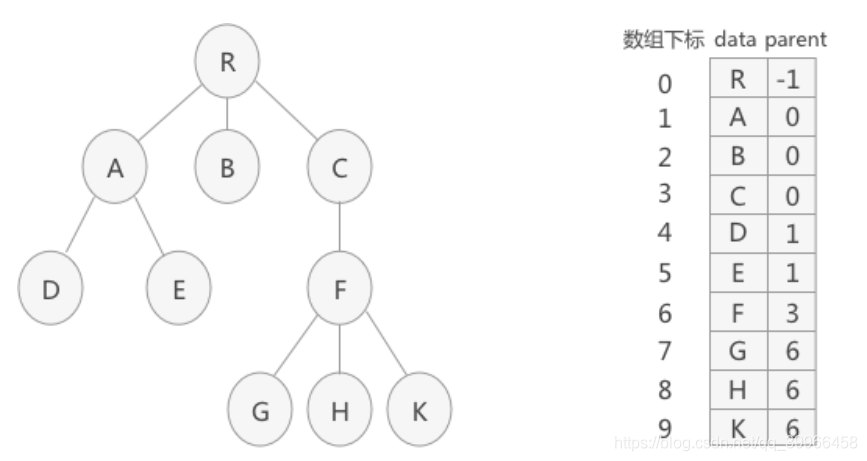
- 代码实现
typedef struct PTNode //结点结构
{
ElemType data;
int parent;//结点的父结点在数组中的位置下标
}PTNode;
孩子表示法
将树中的每个结点的孩子结点排列成一个线性表,用链表存储起来。对于含有 n 个结点的树来说,就会有 n 个单链表,再把 n 个单链表的头指针存储在一个线性表中。如果结点没有孩子,则其单链表为空。

- 代码表示
typedef struct CTNode//每个节点的孩子链表
{
int child; //数据在数组中存储的位置下标
struct CTNode *next;
}*ChildPtr;
typedef struct //每个节点的信息
{
TElemType data;
ChildPtr firstchild; //孩子链表的头指针
}CTBox;
typedef struct//全树
{
CTBox nodes[Tree_Size]; //存储结点的数组
int n, r; //结点数量和树根的位置
}CTree;
孩子兄弟表示法(二叉树表示法)

- 代码表示
typedef struct CSNode
{
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
通过孩子兄弟表示法,普通树转化为了二叉树,所以孩子兄弟表示法又被称为“二叉树表示法”或者“二叉链表表示法”。
森林与二叉树转换
将树转换成二叉树
加线:在兄弟之间加一连线
抹线:对每个结点,除了其左孩子外,去除其与其余孩子之间的关系
旋转:以树的根结点为轴心,将整树顺时针转45°

将二叉树转换成树
加线:若p结点是双亲结点的左孩子,则将p的右孩子,右孩子的右孩子,……沿分支找到的所有右孩子,都与p的双亲用线连起来
抹线:抹掉原二叉树中双亲与右孩子之间的连线
调整:将结点按层次排列,形成树结构

森林转换成二叉树
将各棵树分别转换成二叉树
将每棵树的根结点用线相连
以第一棵树根结点为二叉树的根,再以根结点为轴心,顺时针旋转,构成二叉树型结构

二叉树转换成森林
抹线:将二叉树中根结点与其右孩子连线,及沿右分支搜索到的所有右孩子间连线全部抹掉,使之变成孤立的二叉树
还原:将孤立的二叉树还原成树

树和森林的遍历
树的遍历
遍历
按一定规律走遍树的各个顶点,且使每一顶点仅被访问一次,即找一个完整而有规律的走法,以得到树中所有结点的一个线性排列
常用方法
- 先根(序)遍历:
先访问树的根结点,然后依次先根遍历根的每棵子树 - 后根(序)遍历:
先依次后根遍历每棵子树,然后访问根结点 - 按层次遍历:
先访问第一层上的结点,然后依次遍历第二层,……第n层的结点
森林遍历
- 先序遍历森林
若森林非空:
访问森林中第一棵树的根结点;先序遍历第一棵树根结点的子树森林;
先序遍历除第一棵树后剩余的树构成的森林; - 中序遍历森林
若森林非空:
中序遍历第一棵树根结点的子树森林;访问第一棵树的根结点;
中序遍历除第一棵树后剩余的树构成的森林;
哈夫曼树(Huffman)
带权路径长度最短的树
基本概念
- 路径:从树中一个结点到另一个结点之间的分支构成这
两个结点间的~ - 路径长度:路径上的分支数目
- 树的路径长度:从树根到每一个结点的路径长度之和
- 树的带权路径长度:树中所有带权叶子结点的路径长度之和
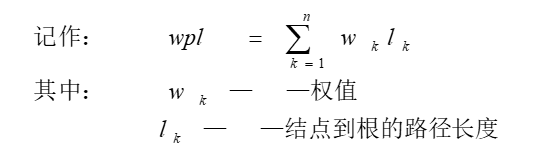
Huffman树
设有n个权值{w1,w2,……wn},构造一棵有n个叶子结点的二叉树,每个叶子的权值为wi,则wpl最小的二叉树叫Huffman树
Huffman算法
- 构造Huffman树步骤
》根据给定的n个权值{w1,w2,……wn},构造n棵只有根结点的二叉树,令其权值为wj。
》在森林中选取两棵根结点权值最小的树作左右子树,构造一棵新的二叉树,置新二叉树根结点权值为其左右子树根结点权值之和。
》在森林中删除这两棵树,同时将新得到的二叉树加入森林中。
》重复上述两步,直到只含一棵树为止,这棵树即哈夫曼树。
Huffman编码
哈弗曼编码是数据通信用的二进制编码
- 思想:根据字符出现频率编码,使电文总长最短
- 编码:根据字符出现频率构造Huffman树,然后将树中结点引向其左孩子的分支标“0”,引向其右孩子的分支标“1”(左0右1);每个字符的编码即为从根到每个叶子的路径上得到的0、1序列


