7.1 图的定义和术语

本篇记录了数据结构图这一章学习的第一部分，
即图的定义和术语。

有向图

• 顶点：数据
• 弧
  表示方法：<v,w>有序对
• 弧头 v
• 弧尾 w

无向图

• 边
• 表示方法：（v,m）无序对
  <>
• 如何表示一个无向图？
  G1 =(V1 , {E1} )
  V1={v1,v2,v3,v4,v5}
  G1=

图的抽象数据类型定义：

ADT Graph{
	数据对象V：顶点集；
	数据关系R：R={VR}
		VR={<v,w>|v,w∈V,且P(v,w), <v,w>表示从v到w的弧，
			P(v,w)定义了弧<v,w>的意义或信息}
}

图的基本操作

1 CreateGraph(&G, V, VR);
初始条件：V是图的顶点集，VR是图中弧的集合
操作结果：按V和VR的定义构造图G
2 DestroyGraph(&G);
初始条件：图G存在
操作结果：销毁图G
3 LocateVex(G,u);
初始条件：图G存在，u和G中顶点有相同特征
操作结果：若G中存在顶点u，则返回该顶点在图中位置；否则返回其它信息。
4 GetVex(G, v);
初始条件：图G存在，v是G中某个顶点
操作结果：返回v的值
5 PutVex(&G, v, value);
初始条件：图G存在，v是G中某个顶点
操作结果：对v赋值value
6 FirstAdjVex(G, v);
初始条件：图G存在，v是G中某个顶点
操作结果：返回v的第一个邻接顶点。若顶点在G中没有邻接顶点，则返回“空”。
7 NextAdjVex(G, v, w);
初始条件：图G存在，v是G中某个顶点，w是v的邻接顶点。
操作结果：返回v的（相对于w的）下一个邻接顶点。若w是v的最后一个邻接点，则返回“空”。
8 InsertVex(&G, v);
初始条件：图G存在，v和图中顶点有相同特征。
操作结果：在图G中增添新顶点v
9 DeleteVex(&G, v);
初始条件：图G存在，v和图中顶点有相同特征
操作结果：删除G中顶点v及相关的弧
10 InsertArc(&G, v, w);
初始条件：图G存在，v和w是G中两个顶点。
操作结果：在G中增添弧<v,w>，若G是无向的，则还增添对称弧<w,v>
11 DeleteArc(&G, v, w);
初始条件：图G存在，v和w是G中两个顶点。
操作结果：在G中删除弧<v,w>，若G是无向的，则还删除对称弧<w,v>
12 DFSTraverse(G, v, Visit( ));
初始条件：图G存在，v是G中某个顶点，Visit是顶点的应用函数。
操作结果：从顶点v起深度优先遍历图G，对每个顶点调用函数Visit一次且仅一次。一旦visit( )失败，则操作失败
13 BFSTraverse(G, v, Visit( ));
初始条件：图G存在，v是G中某个顶点，Visit是顶点的应用函数。
操作结果：从顶点v起广度优先遍历图G，对每个顶点调用函数Visit一次且一次。一旦visit( )失败，则操作失败

子图

• 设有两个图G =（V,E）G1 =（V1,E1）,若V1∈V,
  E1 ∈ E,则称 G1是G的子图；

编辑器打不出集合包含符号，先用∈代替

常见的图

• 1.有向完全图
  n个顶点的有向图最大边数是n(n-1)
• 2.完全图
  n个顶点的无向图最大边数是n(n-1)/2
• 3.稀疏图/稠密图
  边数少为前者，多为后者
• 4.权
  与图的边或弧相关的数为权
• 5.网
  带权的图

顶点的度

• 无向图中，
  顶点的度为与每个顶点相连的边数
• 有向图中，
  顶点的度分成入度与出度
  • 入度：以该顶点为头的弧的数目
    • 出度：以该顶点为尾的弧的数目

邻接点

• 对于无向图G=(V,{E})，如果边 (v,v’)∈E，则称顶点v和v’互为邻接点(Adjacent)，即v和v’相邻接。边(v,v’) 依附(Incident) 于顶点v和v’或者说 (v,v‘)和顶点v和v'相关联。
• 对于有向图G=(V,{A}))，如果弧<v,v’>∈A，则称顶点v邻接到顶点v’,顶点v’邻接自顶点v，弧<v,v’>和顶点v,v’相关联**。

路径

两个顶点之间的顶点序列，该序列的每个顶点与其前驱是邻接点，每个顶点与其后继也是邻接点

• 路径长度——沿路径边的数目或沿路径各边权值之和
• 回路——第一个顶点和最后一个顶点相同的路径叫~
• 简单路径——序列中顶点不重复出现的路径叫~
• 简单回路——除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路叫~

连通图（强连通图）

• 无向图中，若任意两点都存在路径，此图是连通图。
• 有向图中，若任意两点都存在互通路径，此图是强连通图。

连通分量

无向图G的极大连通子图成为G的连通分量。

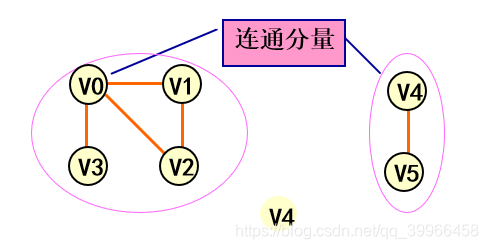
极大连通子图：该子图是G连通子图，将G的任何不在该子图中的顶点加入，子图不再连通。

强连通分量

有向图D的极大强连通子图成为D的强连通分量。

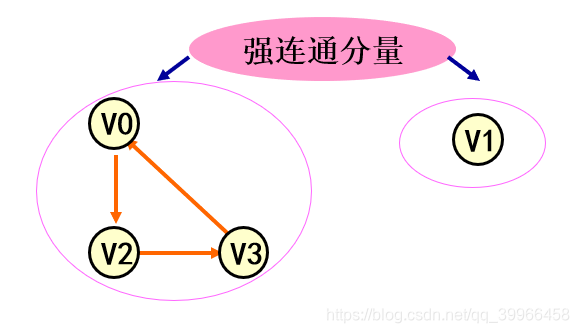
极大强连通子图意思是：该子图是D强连通子图，将D的任何不在该子图中的顶点加入，子图不再是强连通的。

• 下面总结了如何判断连通子图是不是极大或极小连通子图。
  （这个问题好像在离散数学提到过）

若在一个连通子图中，包含了与其中顶点有关所有边（the more the better），则是极大连通子图；若只包含了必不可少的边（the less the better），那就是极小连通子图。

关于此概念，下面的博文讲的很好，上面的总结也是受教于这位博主。
原文链接：https://blog.csdn.net/merlyn_yang/article/details/82467980

版权声明：本文为CSDN博主「merlyn_yang」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

生成树

• 包含无向图G所有顶点的的极小连通子图称为G生成树。
  它含有图中全部顶点，但只有足以构成一棵树的n-1条边。一棵有n个顶点的生成树有且仅有n-1条边。