7.3 图的遍历

BFS、DFS

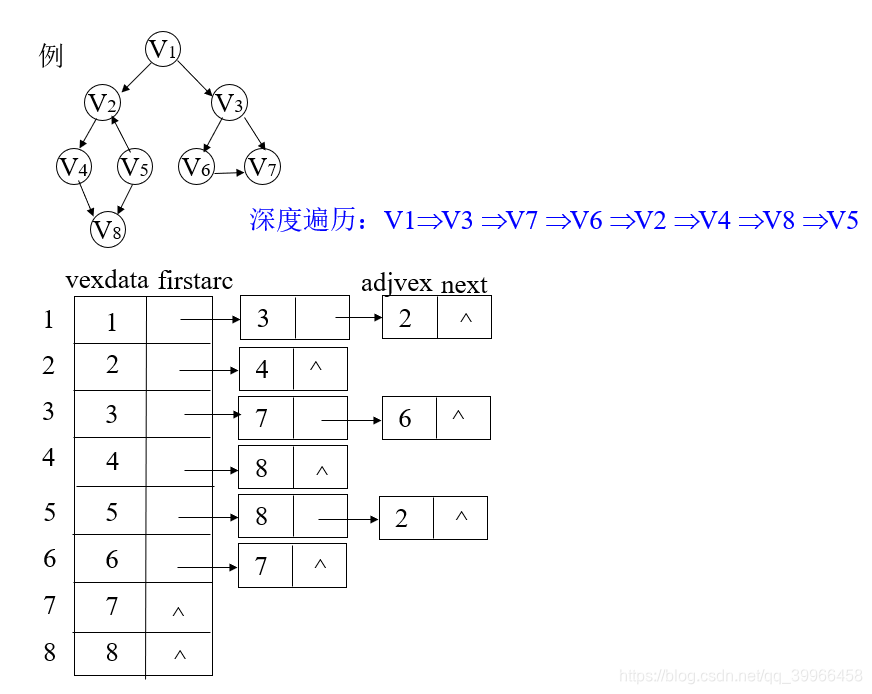
深度优先遍历(DFS)

• 从图的某一顶点V0出发，访问此顶点；然后依次从V0的未被访问的邻接点出发，深度优先遍历图，直至图中所有和V0相通的顶点都被访问到；
  若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止

//--- 下列算法使用的全局变量 ---
Boolean visited[MAX]; // 访问标志数组
Status (* VisitFunc)(int v); // 函数变量

void DFS(Graph G, int v) {
// 从第v个顶点出发递归地深度优先遍历图G。
     visited[v] = TRUE; 
     VisitFunc(v); 
// 访问第v个顶点    
	for(w=FirstAdjVex(G,v);w!=0;w=NextAdjVex(G,v,w))
        if(!visited[w]) 
        	DFS(G, w); 
// 对v的尚未访问的邻接顶点w递归调用DFS
}
void DFSTraverse(Graph G, Status (*Visit)(int v)) {
        // 对图G作深度优先遍历。
       VisitFunc = Visit; 
      for (v=0; v<G.vexnum; ++v) 
             visited[v] = FALSE; // 访问标志数组初始化
      for (v=0; v<G.vexnum; ++v) 
            if (!visited[v]) 
            	DFS(G, v); 
             // 对尚未访问的顶点调用DFS
}

广度优先遍历(BFS)

• 从图的某一顶点V0出发，访问此顶点后，依次访问V0的各个未曾访问过的邻接点；然后分别从这些邻接点出发，广度优先遍历图，直至图中所有已被访问的顶点的邻接点都被访问到；
  若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止

void BFSTraverse( Graph G, status (*visit )(int v ))  {
    for( v = 0; v < G.vexnum; ++v)
        visited[v] = FALSE; 
    InitQueue( Q );
    for( v = 0; v < G.vexnum;  ++ v)
       if( !visited[v] ){
          visited[v] = TRUE;
          visit( v ); 
          EnQueue( Q, v );
          while( !QuqueEmpty( Q))  {
              Dequeue( Q, u ); 
             for(w=FirstAdjVex(G,u);w;w=NextAdjVex(G,u,w))
	            if( !Visited[w] ){
	                Visited[w]=TRUE;
	                Visit( w );
	                Enqueue(Q,w);
                 }// if
	    }// while
      }// if
}// BFSTraverse