【牛客】服务器需求（思维转换角度 线段树）

前言

  Happy Halloween！

题目描述

  小多计划在接下来的n天里租用一些服务器，所有的服务器都是相同的。接下来n天中，第i天需要ai台服务器工作，每台服务器只能在这n天中工作m天，这m天可以不连续。
  但是计划不是一成不变的，接下来有q次修改计划（修改是永久的），每次修改某一天k的需求量ak。
  小多希望知道每次修改之后，最少需要多少台服务器。

输入描述:

  第一行三个正整数n,m,q，分别表示计划的天数，每台服务器能工作的天数和修改次数。
  随后一行n个非负整数，第i个数字ai表示原计划第i天需要多少台服务器工作。
  随后q行，每行两个正整数pi,ci表示把第pi天需要的服务器数目改成ci。

输出描述:

  第一行输出原计划需要的最少服务器数量。
  随后q行，每行输出对应的修改之后，需要的最少的服务器的数量。
示例1
输入
  5 3 2
  1 1 1 1 1
  1 2
  2 3
输出
  2
  2
  3
说明
  未修改时，可以租用2台服务器，分别安排给{1,4,5}和{2,3}这些天。
  当第一次修改时，第一天需要两台服务器，需求变为了2 1 1 1 1，故可以安排成{1,2,3}和{1,4,5}，满足所有的需求。
  第二次修改时，第二天需要三台服务器，需求变为了2 3 1 1 1。可以安排三台服务器，每台服务器安排的日子分别为{1,2,3},{1,2,4}和{2,5}，这样可以满足所有天的需求。

分析

  正着想，将服务器分配给每一天，每天的需求量不同，而且服务器还有限制，不是很好弄。

  不妨换一个角度，考虑将每一天的需求量分给每个服务器

  显然服务器的数量不可能小于最大的需求量

  而且服务器的数量乘以能工作的天数应该大于等于总的需求量

  这样就可以满足条件了

  证明的话。。。。。。

  可以试着构造乱搞的方法

  举一组数据

  5 3 0

  2 3 4 4 5

  显然至少要5个服务器

  可以画出一幅图来分配每台机器第几天做工作

 

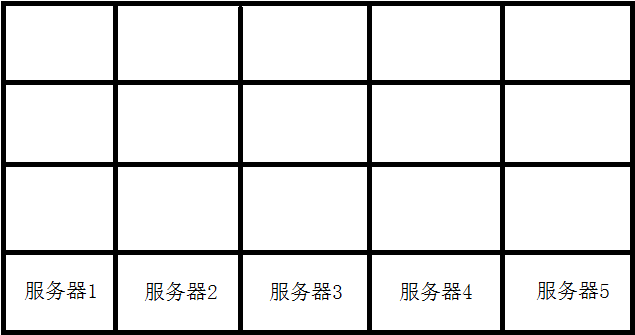
  先把工作量最大的一天分配下去

 

 

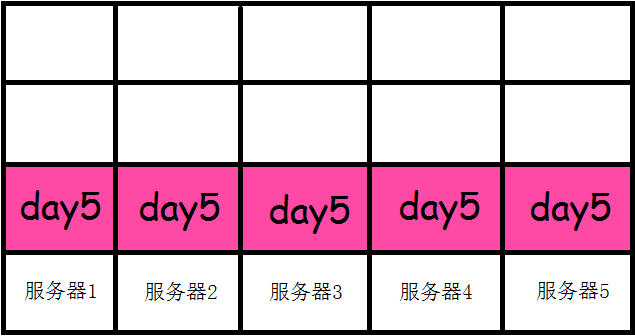
  再把工作量第二大的一天分配下去

 

 

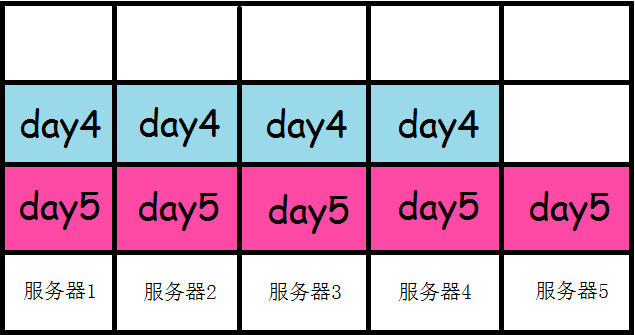
  继续把工作量第三大的一天分配下去

 

 

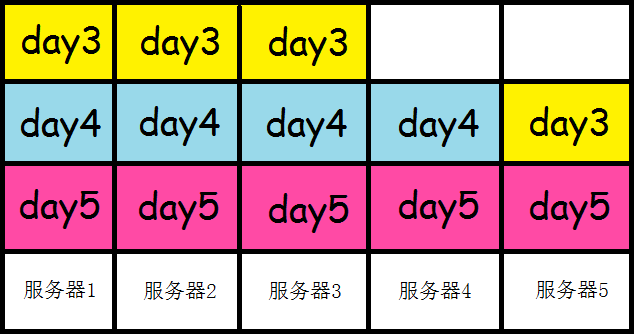
  以此类推，我们可以发现，按照这种分配的方法，只要服务器工作总量大于总的需求量，就一定可以满足题意

  5个的总量是不够的，所以要6个

  所以只需要维护全局最大值，全局和即可。

  懒人直接写线段树了

  Code

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=400005;
long long s[maxn<<2];int n,m,q,mx[maxn<<2];
void fix(int id,int l,int r,int k,int v)
{
    if(l==r){mx[id]=v;s[id]=v;return;}int mid=(l+r)>>1;
    k<=mid?fix(id<<1,l,mid,k,v):fix(id<<1|1,mid+1,r,k,v);
    mx[id]=max(mx[id<<1],mx[id<<1|1]);s[id]=s[id<<1]+s[id<<1|1];
}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1,a;i<=n;i++)scanf("%d",&a),fix(1,1,n,i,a);
    printf("%lld\n",max(1ll*mx[1],s[1]/m+(s[1]%m>0)));
    for(int t=1,p,c;t<=q;t++)
    {
        scanf("%d%d",&p,&c);fix(1,1,n,p,c);
        printf("%lld\n",max(1ll*mx[1],s[1]/m+(s[1]%m>0)));
    }
}